Definiert

Eine Definition (lateinisch Definitio = Abgrenzung aus de = ab/weg und finis = Grenze) ist eine möglichst eindeutige Bestimmung eines Begriffes, des „Definiendum“ (lateinisch „das zu Definierende“). Dazu wird für ein bestimmtes Zeichen eine bestimmte Bedeutung festgesetzt, „Definiens“ genannt (lateinisch „das Definierende“).

In Folge der Übersetzung des klassisch-griechischen Begriffsgefüges in das Lateinische wurde das griech. ορίζειν (ορίζεσθαι) ορισμός in das lateinische Paar definire / definitio und determinare / determinatio aufgespalten. Die definitio (Begriffs-Erklärung) ist vom "Objekt" her, die determinatio (begriffliche Festlegung) vom "Subjekt" her bestimmt; dies ist für die klassisch-griechische Denkform noch in einen einzigen Begriff zusammengefallen.^[1]

Charakter, Zweck und grundsätzliche Bedeutung von Definitionen sowie die Kriterien für deren Eignung oder Fruchtbarkeit werden durch eine besondere Definitionslehre oder im Bereich von Fachsprachen einer Terminologielehre präzisiert. Wenn durch Definitionen Objekte klassifiziert werden, das heißt in eine bestimmte Klasse eingeordnet, wird dadurch eine Taxonomie geschaffen.

Syntax von Definitionen

Prinzipiell bestehen keine syntaktischen Einschränkungen für Definitionen. Jeder Satz, in dem ein neues Zeichen eingeführt wird und der den Kriterien der Eliminierbarkeit und Nichtkreativität genügt, ist eine Definition des neuen Zeichens. Deutlich wird dies mit der Definition der Modulo-Äquivalenz:

$a \equiv b \pmod{m} :\iff \bigvee_{n \in \mathbb{N}}(a-b=n\cdot m)$

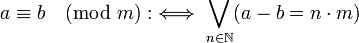
Die weitverbreitetste Form von Definitionen stellt die Definitionsgleichung dar.

Beispiel:

Dattel ≡ die Frucht der Palme; Lagmy ≡ der Wein der Palme; Wein ≡ gegorener Saft

Wenn man sich das Grundmuster einer Definition ansieht, so ist in Gestalt eines Satzes formuliert, was die Definitionsaussage enthält. Diese informiert uns darüber, dass eine bestimmte Beziehung zwischen Begriffen vorliegt und wie bestimmte Regeln eingesetzt werden können.^[2]

Der Ausdruck, der definiert werden soll, heißt "Definiendum" (lateinisch „das zu Definierende“) und steht links vom Äquivalenzzeichen (≡). In unserem Beispiel sind „Dattel“, „Lagmy“ und „Wein“ die Definienda.

Der Satzteil, der die definitorische Erklärung liefert, „Definiens“ genannt (lateinisch „das Definierende“), steht rechts vom Äquivalenzzeichen (≡). „Dattel“ ist also dadurch definiert, dass es dasselbe bedeuten soll wie „die Frucht der Palme“.

Sinn und Zweck des Definierens

Definitionen werden von uns selber festgesetzt und sind demnach nichts weiter als sprachliche Konventionen; und nicht etwa Behauptungen. So können sie daher auch nicht wie Behauptungen wahr oder falsch sein. Man nennt sie daher auch "willkürlich" (englisch wilfully), weil sie von unserem Willen abhängen bzw. vom Willen des Sprechers, der sie benutzt. Das ist jedoch nicht dasselbe wie „Beliebigkeit“ (englisch arbitrariness). Denn auch beim Definieren ist es sinnvoll, dass wir von unserem Ermessensspielraum zweckmäßig Gebrauch machen und uns hierbei an bestimmte Regeln halten.

Definitionen werden häufig gefordert und für nötig gehalten, um eine Verständigung über die benutzten Wörter und Begriffe herbeizuführen beziehungsweise um Missverständnisse möglichst von vornherein auszuschließen. Das ist aber nicht immer einfach zu bewerkstelligen, denn auch die zum Definieren benutzten Wörter können leicht ihrerseits wieder zu Missverständnissen Anlass geben. So bemüht sich die Rechtswissenschaft, die in Gesetze benutzten Begriffe durch andere Begriffe zu definieren und so auf konkrete Streitfälle anwendbar zu machen. Da aber auch die anderen Begriffe jeweils auslegungsbedürftig sein können und ihrerseits einer Definition bedürfen, führt dies zu einem „infiniten Regress“ im Definieren.

Als erstes gilt es somit zu überlegen, zur Lösung welcher Probleme überhaupt man Definitionen einsetzen will: Worüber will man sprechen? Welche Frage will man klären? Man wird sich nicht auf eine Definition einigen können, solange man nicht über den Gegenstand derselben Einigung erzielt hat.

Wohl bei keiner Problemstellung fängt man ganz von vorne, beim Nullpunkt, an. Es liegen immerzu bereits Formulierungen der Ausgangsfrage und von Antwortversuchen vor, worin Begriffe schon und deren Definitionen benutzt werden. Wenn man mit den vorhandenen Formulierungen der Problemstellung und der Lösungsversuche arbeitet und sie dabei kritisch überprüft, werden meist auch die vorhandenen Begriffe deutlicher und können sodann überarbeitet werden, etwa in dem „Explikation“ genannten Verfahren.

Wenn Definitionen am Beginn der eigenen Überlegungen stehen, wo also noch gar nicht der Gegenstand derselben vollständig erkannt ist, kann eine Definition schwerlich vollständig und endgültig sei.^[3] Man wird daher mit einer Art von "Arbeitsdefinition" beginnen. Eine Endfassung kann erst nach Abschluss der theoretischen Arbeit geliefert werden, gleichsam als das Resultat, in dem die Lösung der Problemstellung zusammengefasst wird.

Der Stellenwert von Definitionen wird letztendlich bestimmt durch die Definitionslehre, der man zu folgen sich entscheidet. Dabei ist die Grundsatzentscheidung zu treffen, ob dem Begriff oder der Aussage, den Wörtern oder den Sätzen der logische Vorrang zuerkannt werden soll, beziehungsweise ob das Endprodukt unseres Erkenntnisprozesses aus Definitionen oder aus Theorien bestehen soll.

Für die Wissenschaftstheorie von Karl Popper^[4] oder zunächst auch von Wolfgang Stegmüller^[5] ist Wissenschaft nicht ein System von Begriffen, sondern ein System von Sätzen.^[6] Die Methodologie des Kritischen Rationalismus setzt an die Stelle der herkömmlichen Begriffsorientierung die Problemorientierung. Die Bedeutung von Definitionen tritt zurück gegenüber der Konstruktion von Theorien und, aus diesen logisch ableitbar, der Aufstellung empirisch falsifizierbarer Hypothesen.^[7] Um Hypothesen durch empirische Daten widerlegen zu können, müssen die fraglichen Begriffe oder Begriffskonstrukte in eine messbare Form überführt werden. Es stellt sich somit die Aufgabe der Operationalisierung.

Hingegen nach einer alternativen Wissenschaftstheorie, non-statement view genannt, die Wolfgang Stegmüller von John D. Sneed übernommen hat, sind Theorien keine Satzmengen, sondern Begriffe. Erst die mit Theorien verbundenen Anwendungsbehauptungen kommen dann für Bestätigungen oder Widerlegungsversuche in Frage.^[8]

Funktionen von Definitionen in der Wissenschaft

• Wissenschaftliche Definitionen werden in der Regel dann gefordert, wenn Hypothesen und Theorien aufgestellt oder Modelle konstruiert werden, die von anderen Wissenschaftlern nachvollzogen und diskutiert werden können sollen. Um den Kriterien der Intersubjektivität zu genügen, soll hierbei Einvernehmen über die Bedeutung der verwendeten Begriffe erzielt werden. – Nach der Definitionslehre von Karl Popper hingegen wird die Definitionsfrage dadurch miterledigt, dass man die Theorie als Ganzes auf einen Objektbereich anwendet und einzelnen Folgerungen daraus an Beobachtungssätzen überprüft.
• Definitionen sind Abkürzungen und erleichtern daher zu formulieren und sich besser verständlich zu machen.
• Definitionen sind als Festsetzungen weder wahr noch falsch. Sie erleichtern es jedoch, entsprechende Aussagen einfacher, das heißt verständlicher, zu formulieren.

Arten von Definitionen

Deiktische Definition

Die elementarste Form der Definition ist die Bestimmung eines Begriffs durch hinweisendes Zeigen auf einen Vertreter für ihn: Das, worauf ich hier zeige, sei ein Beispiel für ein X. (siehe Deixis)

Explizite gegenüber implizite Definition

Das Grundmodell ist die explizite Definition, wie sie in einer Definitionsgleichung erfolgt. Im weiteren Sinne können noch Definitionen hierzu gerechnet werden, die sich in eine solche Grundform überführen lassen.^[9] Regel: Das Definiendum darf im Definiens selbst nicht vorkommen.

Beispiele hierfür sind die im Bereich der Rechtswissenschaft gebräuchlichen Legaldefinitionen. So wird der zivilrechtliche Begriff „unverzüglich“ in § 121 BGB mit den Worten „ohne schuldhaftes Zögern“ legaldefiniert. Der Begriff "schuldhaft" wird sodann in §§ 276 bis 278 BGB definiert; die dort verwendeten Begriffe von Vorsatz und Fahrlässigkeit sind ihrerseits Gegenstand der Begriffsarbeit in der Rechtslehre, also außerhalb des Gesetzeswortlautes.

Im Gegensatz dazu steht die implizite Definition. Dort wird ein Objekt durch seine charakteristische Eigenschaft festgelegt. Dazu muss nachgewiesen werden, dass diese Eigenschaft genau einem Objekt zukommt (Wohldefiniertheit). Beispiel: „Die Quadratwurzel aus einer nicht-negativen reellen Zahl x ist definiert als diejenige nicht-negative relle Zahl y, für die gilt x = y².“ Die Wohldefiniertheit dieser impliziten Definition besagt, dass es für jede nicht-negative reelle Zahl x genau eine nicht-negative relle Zahl y gibt mit der Eigenschaft x = y².

Als Grenzfall einer Definition kann man die implizite Definition durch ein monomorphes Axiomensystem ansehen. Indem dem, was in den Axiomen formal fixiert ist, jeweils ein Name gegeben wird, ist die semantische Seite des Systems festgelegt, d.h. was es für uns bedeuten soll. Die Begriffe jedoch werden strukturell exakt durch die Einordnung in die Axiome und damit in das axiomatische System bestimmt.^[10]

Rekursive Definition

Die rekursive Definition - veraltet auch induktive Definition genannt - unterscheidet sich von der expliziten Definition dadurch, dass das Definiendum im Definiens vorkommt. Rekursive Definitionen eignen sich dazu, den Wert einer mathematischen Funktion auf den Wert derselben Funktion an einer kleineren Stelle zurückzuführen. Auch hier muss die Wohldefiniertheit nachgewiesen werden, damit die Definition zulässig ist. Das geschieht in Form von Rekursionstheoremen, die nachweisen, dass durch wiederholtes Anwenden der Definition kein Infiniter Regress stattfindet.

Identität gegenüber Gebrauchsdefinition

Man spricht von Gebrauchsdefinition (oder Kontextdefinition), weil das Definiendum darin nur so definiert wird, wie man es innerhalb von Sätzen gebraucht.

Fällt beispielsweise eine allgemeine Definition des Prädikates „adäquat“ schwer, so lässt sich leicht definieren, dass die Aussage „X ist ein adäquater Kalkül“ genau dann wahr ist, wenn X ein Kalkül ist, der vollständig und korrekt ist.

Adäquatheit wurde damit nur im Kontext „Kalkül“ definiert, und die Frage, wann überhaupt etwas adäquat ist, bzw. welche Dinge unter diesen Begriff fallen, stellt sich nicht. Dieser ontologische Unterschied erspart etwa der modernen Mathematik die philosophische Frage nach dem Wesen der Zahl (empirisch, psychologistisch oder logisch). Denn die mathematischen Axiome sagen nicht, was eine Zahl ist, sondern wann sich etwas Zahl nennen darf und welche arithmetischen Eigenschaften sodann für diese gelten.

Dass zum Beispiel die Gruppenaxiome gerade davon leben, dass sie verschiedenste Interpretationen erlauben, widerspricht übrigens der klassischen Anschauung, Definitionen müssten eindeutig sein.

Totale gegenüber partielle Definition

In "totalen Definitionen" sind Definiendum (das zu Definierende) und Definiens (das Definierende) äquivalent.

In "partiellen Definitionen" gilt dies nur für einen bestimmten Teilbereich, das heißt nur für den Fall, dass eine gewisse Vorbedingung erfüllt ist.

"Operationale Definitionen" sind häufig partiell. Hier stellt die Vorbedingung eine Operation dar, womit man die zu definierende Eigenschaft überprüft.

Die dazu gehörige Gattung der "Dispositionsbegriffe"^[11] (wie zum Beispiel „wasserlöslich“) beschreibt keine Eigenschaften, die direkt durch Beobachtung ablesbar sind, sondern ist an eine (Prüf-) Bedingung geknüpft.

Zum Beispiel: Wenn man den Gegenstand in Wasser gibt, dann löst er sich auf.

Nominal- gegenüber Realdefinitionen

Durch die früher stark verbreitete aristotelische oder scholastische Definitionslehre werden herkömmlicherweise Nominal- und Realdefinitionen unterschieden:

Mittels einer Nominaldefinition setzt der jeweilige Sprecher durch seine eigene Entscheidung fest, was ein Name benennen bzw. ein sprachlicher Ausdruck bedeuten soll. (siehe Hauptartikel Nominaldefinition)

Eine Realdefinition beansprucht auszusagen, was eine Sache in Wirklichkeit sei.

Eine Nominaldefinition kommt in der Verwendung der heute üblichen "Explizitdefinition" gleich.

Die Realdefinition beinhaltet bestimmte theoretische oder philosophische Voraussetzungen, etwa was bestimmte Dinge sind oder welche es überhaupt gibt und wie sie geordnet sind (Ontologie). Es werden dabei in der Regel Unterschiede der Art und der Gattung nach gemacht (Taxonomie).

Hinter dem Gebrauch von Realdefinitionen steht mehr oder minder ausdrücklich eine bestimmte philosophische Auffassung von Sein und Wesen (Essentialismus) oder Annahmen über das Vorliegen einer bestimmten Gesetzmäßigkeit, die im Wesen der Sache ihren Ausdruck finde.

Weniger verfänglich ist es, Realdefinitionen dem Verfahren der Bedeutungsanalyse oder Explikation zu unterziehen. Das Ergebnis eines solchen Explikationsversuchs kann dann wie eine explizit eingeführte Definition behandelt werden, ohne dass man sich dabei unbedingt auf eine bestimmte Philosophie festlegen muss.

Definitionsregeln und -anforderungen

Welche Regeln des Definierens man einhält, ist abhängig davon, welcher Definitionslehre zu folgen man sich entschieden hat.

In den nicht formalen Wissenschaften werden meist folgende Anforderungen für sinnvoll angesehen:

• Die Anzahl unterschiedlicher Interpretationsmöglichkeiten soll so weit wie möglich reduziert werden.
• Dennoch soll eine Definition so einfach wie möglich sein.
• Eine Definition ist umso besser, je schärfer die Grenzen zu anderen Begriffen gezogen sind.
• Es dürfen nur Begriffe verwendet werden, die schon als Allgemeinbegriff eindeutig sind oder die bereits innerhalb derselben Wissenschaft definiert sind.
• Eine Definition soll möglichst keine Ausnahmeregeln enthalten.
• Definitionen sind weder wahr noch falsch; doch Realdefinitionen sollten (nach Carnap) diese vier Kriterien zur Adäquatheit erfüllen:
  1. Ähnlichkeit von Explikat und Explikandum
  2. Exaktheit des Explikats
  3. Fruchtbarkeit für das Aufstellen vieler Gesetze
  4. Einfachheit der Definition selbst und der resultierenden Gesetze

Beispiele

• Deiktische Definition: Dies hier ist rot: rot
• Realdefinition: "Lagmy" ≡ Wein, der hergestellt wird aus der Vergärung des Saftes der Dattelpalme
• Nominaldefinition: Unter "AWT" sei im nachfolgenden Text "Arbeitswerttheorie" verstanden.
• Gebrauchsdefinition:: „n ist Primzahl 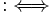$:\iff$ n ist eine natürliche Zahl und besitzt genau zwei natürliche Teiler.“
• Rekursive Definition: „Die Summe sum(n) der ersten n natürlichen Zahlen ist definiert als 0, falls n = 0 und sum(n − 1) + n sonst.“
• Induktive Definition: „Eine natürliche Zahl n heißt gerade, wenn n = 0 gilt oder wenn 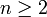$n\ge 2$ und n − 2 gerade ist.“
• Empirische Definition, besser: empirische Analyse: „Der Mensch ist ein ungefiederter Zweibeiner.“

Siehe auch

• Definitio essentialis
• Definitio abundans
• Substantielle Definition
• Genus proximum et differentia specifica (Definition durch Angabe eines Oberbegriffs und eines spezifischen Artmerkmals)

• Prädikat (Logik)
• Terminus
• Terminologie
• Operationalisierung
• Guidelines for the Definition of Managed Objects

• Rekursion
• Definitionsmacht
• Dogmatische Definitionen: siehe Dogmatik

Quellen

1. ↑ Johannes Lohmann: Vom ursprünglichen Sinn der aristotelischen Syllogistik. In: Fritz-Peter Hager (Hrg.): Logik und Erkenntnislehre des Aristoteles. Wissenschaftliche Buchgesellschaft, Darmstadt 1972, S. 193, Anmerkung 14, ISBN 3-534-04552-1.
2. ↑ Georg Klaus: Moderne Logik. Berlin 1972, S. 384.
3. ↑ John Stuart Mill: A System of Logic. London Colchester 1959; S. 1
4. ↑ Karl R. Popper. Logik der Forschung. Tübingen 8. verb. u. verm. Aufl. 1984, S. 9.
5. ↑ „Es ist zweckmäßiger, Sätze und nicht Wörter als die ursprünglichen sinnvollen Einheiten der Sprache aufzufassen. Denn Sätze oder Aussagen und nicht Wörter sind es, die wir im alltäglichen und wissenschaftlichen Gespräch behaupten und bestreiten; und nur Sätzen kommt einer der Wahrheitswerte wahr oder falsch zu." (Wolfgang Stegmüller: Probleme und Resultate der Wissenschaftstheorie und Analytischen Philosophie, Bd. I: Wissenschaftliche Erklärung und Begründung. Berlin, Heidelberg, New York (verb. Nachdruck) 1974, S. 6.)
6. ↑ So stand schon in der Logik beginnend mit Gottlob Frege der einfache Satz im Mittelpunkt der Betrachtung. (Jürgen Habermas: Wahrheit und Rechtfertigung. Frankfurt/Main 2004. ISBN 3-518-29323-0. S. 77)
7. ↑ „Unter einer brauchbaren Wissenschaftslogik verstehen wir eine solche, die an die Stelle der alten Begriffsorientierung die Problemorientierung setzt, die die Akzentuierung von Definitionen zugunsten der Betonung von Hypothesen und Theorien fallen lässt, die vom konservativen Gebrauch methodologischer Überlegungen zur Dogmatisierung traditioneller Denkformen, Verfahrensweisen und Perspektiven zu ihrem kritischen Gebrauch übergeht und an die Stelle des statischen Gesichtspunktes einer Rechtfertigung des Bestehenden den dynamischen einer Förderung der Entwicklung durch kritische Diskussion setzt." (Hans Albert (Hrg.): Theorie und Realität. Tübingen, 1. Auflage 1964, S. 14.)
8. ↑ Joseph S. Sneed: The Logical Structure of Mathematical Physics. Dordrecht 1971; Wolfgang Stegmüller: Theorie und Erfahrung. Zweiter Halbband: Theorienstruktur und Theoriendynamik. Berlin Heidelberg New York 1973
9. ↑ Georg Klaus: Moderne Logik. Berlin 1972, S. 384.
10. ↑ Georg Klaus: Moderne Logik. Berlin 1972, S. 385 f.
11. ↑ zur methodologischen Funktion der Dispositionsbegriffe vergleiche Paul Feyerabend: Das Problem der Existenz theoretischer Entitäten. In: Ernst Topitsch (Hrsg.): Probleme der Wissenschaftstheorie. Festschrift für Viktor Kraft. Wien 1960.

Literatur

• Walter Dubislav: Die Definition. Meiner, 4. Auflage, Hamburg 1981 (Klassiker).
• Gottfried Gabriel: Definition II. In: Ritter (Hrsg.): Historisches Wörterbuch der Philosophie. 1972, Sp. 35-42.
• Gottfried Gabriel: Definition. In: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. 2. Auflage 2005, S. 137–139.
• N. Kondakow: Wörterbuch der Logik. Leipzig, 2. Auflage 1983.
• Guy Longworth: Definitions, Uses and Varieties of, wahrscheinlich 2008 erschienen in: K. Brown (Hrsg.): Elsevier Encyclopedia of Language and Linguistics. Elsevier.
• Albert Menne: Definition. In: Krings, Baumgartner, Wild: Handbuch philosophischer Grundbegriffe. 1973.
• Lothar Schmidt: Schlagfertige Definitionen. Von Aberglaube bis Zynismus. Auswahl. 1971, ISBN 3-499-16186-9.
• Wolfgang Stegmüller: Probleme und Resultate der Wissenschaftstheorie und Analytischen Philosophie. Band I: Wissenschaftliche Erklärung und Begründung. Springer, Berlin u. a. 1974 (verbesserter Nachdruck).
• Greta Stanaityte: Alltagsdefinitionen und ihre Funktionen. Dissertation, Universität Mannheim 2005 (Volltext).

Weblinks

• Anil Gupta: „Definitions“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• Kants Äußerungen über das Definieren im Kant-Lexikon von Rudolf Eisler