Diaconis

Persi Warren Diaconis (* 31. Januar 1945 in New York City) ist ein US-amerikanischer Mathematiker, der sich vor allem mit Statistik und Wahrscheinlichkeitstheorie befasst. Außerdem war er als Magier bekannt.

Leben und Werk

Diaconis stammt aus einer Familie professioneller Musiker, und auch Diaconis nahm neun Jahre Geigenstunden u.a. an der Juilliard School. Er verließ vorzeitig mit 14 Jahren die Schule (er war gerade am City College in New York eingeschrieben), um Zauberkünstler zu werden, auf Einladung des bekannten Magiers Dai Vernon. Zwei Jahre später war er professioneller Magiker, der eigene Tricks erfand (einige seiner Kartentricks wurden in Martin Gardners Kolumne im Scientific American veröffentlicht) und unterrichtete. Nach eigenen Aussagen wechselte er zur Mathematik, da er William Fellers klassisches Lehrbuch der Wahrscheinlichkeitstheorie und Statistik benutzen wollte, aber nichts davon verstand. Er nahm Abendkurse am New York City College und machte 1971 seinen Abschluss in Mathematik. Er wurde im Graduate Program für Statistik an der Harvard University akzeptiert und wurde 1974 bei Dennis Hejhal promoviert (Weak and Strong Averages in Probability and the Theory of Numbers). Danach ging er zur Stanford University, wo er noch heute Professor ist.

1979 und 1982 erhielt er ein Stipendium der MacArthur Foundation. 1990 war er Invited Speaker auf dem Internationalen Mathematikerkongress (ICM) (Application of group representations to statistical problems) und ebenso 1998 in Berlin (From Shuffling Cards to Walking around the Building: Introduction to Markov Chain Theory).

Diaconis befasste sich z.B. mit Zufallsmatrizen, Benfords Gesetz^[1], Irrfahrten (Random Walks) auf Gruppen und Kartenmischungen. So zeigte er mit Dave Bayer, dass mindestens sieben „Shuffles“ (perfekte Mischungen) nötig sind, um 52 Spielkarten annähernd zufällig zu verteilen (und für n Karten mindestens 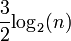$\frac{3}{2} {\rm log}_2(n)$ Mischungen)^[2]. Diaconis war auch aktiv in der Aufdeckung von Manipulationen in der Parapsychologie^[3] und in der Sphäre professionellen „Glücksspiels“. Mit Joseph Keller untersuchte er „faire“ Würfel (symmetrische und unsymmetrische mit beliebig vielen Seiten), und bewies z.B. dass es keine fairen symmetrischen Würfel mit fünf Seiten gibt (dafür aber unsymmetrische)^[4].

Schriften

• Group representations in probability and statistics. Institute of Mathematical Statistics, Hayward, 1988, ISBN 0-940600-14-5.
• Theories of data analysis: from magical thinking through classical statistics. In: D.Hoaglin, Mosteller, Tukey (Herausgeber): Exploring Data Tables, Trends and Shapes. Wiley 1985.
• Patterns in eigenvalues. Bulletin AMS 2003, Gibbs Lecture.
• Interview in Statistical Science, August 1986, S.319
• From Shuffling Cards to Walking Around the Building: An Introduction to Modern Markov Chain Theory. ICM 1998.

Literatur

• Interview in Albers, Alexanderson: Mathematical People. 1985.

Weblinks

• Homepage in Stanford
• Biografie

• Stanford News zu Diaconis
• Bibliographie von Diaconis
• zu Diaconis Ergebnissen bei Kartenmischungen
• Pressebericht zu Diaconis auf dem ICM 1998

Einzelnachweise

1. ↑ The Distribution of Leading Digits and Uniform Distribution Mod 1. Annals of Probability, Bd.5, 1977, S. 72-81.
2. ↑ D. Bayer, Diaconis: Trailing the Dovetail Shuffle to Its Lair. Annals of Applied Probability, Bd.2, 1992, S. 294–313. Diaconis, David Aldous: Shuffling Cards and Stopping Times. American Mathematical Monthly, Bd.93, Mai 1986, S.333. Siehe auch Rifle Shuffle bei Math World
3. ↑ Statistical problems in ESP research. Science, Bd.201, 1978, S.131-136.
4. ↑ Diaconis, Keller: Fair Dice. American Mathematical Montly, Bd.96, April 1989, S.337.

Personendaten
NAME	Diaconis, Persi
KURZBESCHREIBUNG	US-amerikanischer Mathematiker
GEBURTSDATUM	31. Januar 1945
GEBURTSORT	New York City