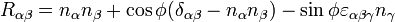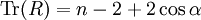- Drehungsmatrix
-
Eine Drehmatrix oder Rotationsmatrix ist in der Mathematik eine Matrix, die eine Drehung im euklidischen Raum beschreibt.
Die Drehung kann entweder ein Objekt (eine Figur, einen Körper) bezüglich eines festgehaltenen Koordinatensystems oder das Koordinatensystem selbst bewegen.
Inhaltsverzeichnis
Drehmatrix der Ebene R²
In der euklidischen Ebene
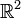 wird die Drehung eines Vektors p um den Ursprung um den Winkel α, welcher im mathematisch positiven Sinn (gegen den Uhrzeigersinn) definiert ist, realisiert durch die Multiplikation mit der Drehmatrix R.
wird die Drehung eines Vektors p um den Ursprung um den Winkel α, welcher im mathematisch positiven Sinn (gegen den Uhrzeigersinn) definiert ist, realisiert durch die Multiplikation mit der Drehmatrix R.Bei der aktiven Drehung wird der Vektor durch die Multiplikation eines Vektors mit der Matrix R gedreht:
- p2 = Rp1
Bei der passiven Drehung wird das Koordinatensystem gedreht. Die Koordinaten des Vektors im gedrehten Koordinatensystem findet man durch Multiplikation mit der Matrix R − 1:
- p2 = R − 1p1
Die Elemente der Drehmatrizen ergeben sich folgendermaßen: Bezeichnen wir mit p1 den Vektor vor und mit p2 den Vektor nach der Rotation.
Für die Koordinaten x1 und y1 bedeutet dies:
- x1 = cosφ
- y1 = sinφ.
Nach den Additionstheoremen ergibt sich damit für die neuen Koordinaten x2 und y2 nach einer Drehung um den Winkel α:
und damit in Matrix-Schreibweise
mit der aktiven Drehmatrix R. Durch ähnliche Überlegungen erhalten wir die passive Matrix R − 1
Positive Winkel werden in der Mathematik üblicherweise mit Hilfe der sogenannten Rechten-Daumen-Regel definiert. Dagegen ist die Verwendung des Uhrzeigersinns eine nicht hinreichende Bedingung zur Bestimmung des Winkels. Erfolgt die Drehung entgegen dem mathematisch positivem Drehsinn, dann ist der Winkel bei der Berechnung negativ einzugeben.
Drehmatrizen des Raumes R³
Die elementaren Drehungen im
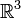 sind Drehungen um die üblichen kartesischen Koordinatenachsen. Folgende Matrizen drehen einen Punkt (bzw. Vektor) um den Winkel α.
sind Drehungen um die üblichen kartesischen Koordinatenachsen. Folgende Matrizen drehen einen Punkt (bzw. Vektor) um den Winkel α.Bitte beachten: Diese Matrizen drehen nicht die Koordinatenachsen - wie z.B. in der Physik üblich. Um solche Drehmatrizen zu erhalten, müssen bei den untenstehenden einfach die Vorzeichen aller Sinus-Einträge vertauscht werden.
- Drehung eines Punkts mit x-Achse als Drehachse:
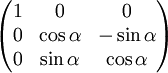 ,
,
- Drehung eines Punkts mit y-Achse als Drehachse:
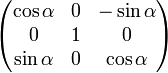 ,
,
- Drehung eines Punkts mit z-Achse als Drehachse:
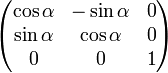 ,
,
Diese Matrizen gelten sowohl für Rechts- als auch für Linkssysteme. Drehungen mit positiven Drehwinkeln sind im Rechtssystem Drehungen entgegen dem Uhrzeigersinn. Im Linkssystem wird bei positiven Winkeln mit dem Uhrzeigersinn gedreht. Der Drehsinn ergibt sich, wenn man entgegen der positiven Drehachse auf den Ursprung sieht. In Rechtssystemen kann auch eine rechte-Hand-Regel angewandt werden: Zeigt der Daumen der rechten Hand in Richtung der Drehachse, so geben die gebeugten restlichen Finger die Richtung des Drehwinkels an.
- Drehung mit beliebigem Einheitsvektor v=(v1,v2,v3)T als Drehachse:
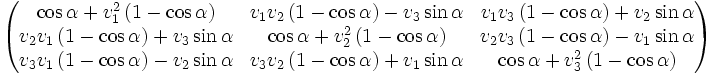 .
.
Diese beliebige Drehung lässt sich auch über drei aufeinanderfolgende Drehungen mit den Eulerschen Winkeln um bestimmte Koordinatenachsen erzielen, so dass sich diese Matrix auch mit diesen Winkeln formulieren lässt.
Allgemeine Definition
Eine
 -Matrix R mit reellen Komponenten heißt Drehmatrix, wenn sie
-Matrix R mit reellen Komponenten heißt Drehmatrix, wenn sie- a) die Länge von Vektoren und die Winkel zwischen Vektoren erhält (ausgedrückt durch das Skalarprodukt), wenn also für alle Vektoren x und y des
 gilt:
gilt:
und
- b) orientierungserhaltend also
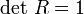 ist.
ist.
Drehmatrizen sind orthogonale Matrizen mit der Determinante +1. Die Menge aller Drehmatrizen eines Raumes bildet die spezielle orthogonale Gruppe.
Die Drehmatrix ist im allgemeinen definiert als:
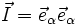 Einheitsmatrix
Einheitsmatrix
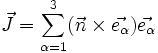 Erzeugende einer infinitesimalen Drehung
Erzeugende einer infinitesimalen Drehung
und die Elemente werden definiert als:
Eigenschaften
Weitere Eigenschaften von
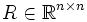 :
:- det(R) = 1 (Determinante)
- RT = R − 1 (R transponiert = R invertiert)
- RTR = RRT = Idn (orthogonal)
- Die Ausrichtung des Koordinatensystems (Rechts- oder Linkssystem) wird beibehalten.
- Die Drehachse
 ist die Lösung zu:
ist die Lösung zu:
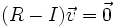 .
.
Da (R − I) singulär ist, ist die Berechnung der Drehachse über eine Eigenwertzerlegung durchzuführen. Die Drehachse
 ist Eigenvektor von R mit Eigenwert 1.
ist Eigenvektor von R mit Eigenwert 1.- Der Drehwinkel α ergibt sich über das Skalarprodukt:
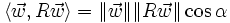 ,
,
mit
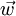 orthogonal zur Drehachse
orthogonal zur Drehachse 
oder aus der Spur der Drehmatrix (für den Fall
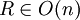 )
)(siehe auch Formel für die Matrix einer Drehung um eine allgemeine Achse oben).
Wikimedia Foundation.

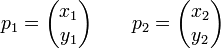
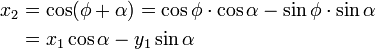
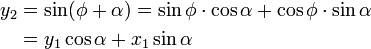
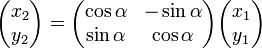
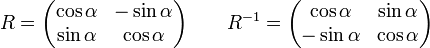
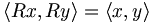
![R = \vec{n}\cdot\vec{n}+\cos\phi[\vec{I}-\vec{n}\cdot\vec{n}]+\sin\phi \vec{J}](/pictures/dewiki/51/3944b70e7423525c5b2fe22033abc8c0.png)