Dreizehn-Knoten-Seil

Allegorie der Arithmetik mit Rechenseil (aus dem Hortus Deliciarum (um 1180)

Das Rechenseil oder Knotenseil war eine gebräuchliches Rechenhilfsmittel des Mittelalters, mit Hilfe dessen man verschiedene mathematische und geometrische Probleme einfach lösen konnte.

Als allegorische Personifizierung der Arithmetik bei der Darstellung der freien Künste diente eine weibliche Figur mit dem Attribut des Knotenseils.

Ein Rechenseil hatte im allgemeinen mindestens 12 Knoten (daher auch oft Zwölfknotenschnur^[1]^[2]^[3] genannt) in gleichem Abstand. Mehr Knoten waren speziell für die Multiplikation und Division von Vorteil.

Im Bauwesen des Mittelalters war das Rechenseil für die Architekten unverzichtbar, da damit einfach gleichseitige und rechtwinklige Dreiecke sowie Kreise konstruiert werden können.

Rechenfunktionen

Arithmetik
Addition	X + Y = Z	Man zählt erst X Knoten ab, dann Y weitere. Die Gesamtzahl der abgezählten Knoten ist Z.	Bsp: 5 + 4 = 9
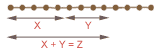
Subtraktion	X - Y = Z	Man zählt erst X Knoten ab und geht dann Y zurück. Die Gesamtzahl der abgezählten Knoten ist Z.	Bsp: 9 - 4 = 5
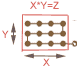
Multiplikation	X * Y = Z	Man zählt X Knoten ab und legt diese Strecke Y mal zusammen. Die Gesamtzahl der abgezählten Knoten ist Z.	Bsp: 4 * 3 = 12
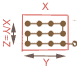
Division	X / Y = Z (Rest Q)	Man zählt X Knoten ab. Davon nimmt man Y und legt diese so oft zusammen, bis alle aufgebraucht sind. Die Anzahl der Zusammenlegungen ist Z. Übrig gebliebene Knoten sind der Rest Q.	Bsp: 13 / 4 = 3 Rest 1
Geometrie
Rechter Winkel	4² + 3² = 5² 16 + 9 = 25 (Pythagoras)	Man nagelt Anfang und Ende des Rechenseils zusammen. Für die Grundseite zählt man 5 ab (4 Teilstrecken) und nagelt dieses fest. Für die Senkrechte darauf benötigt man 4 Knoten (3 Teilstrecken). Durch das Spannen dieser Seiten entsteht ein rechtwinkliges Dreieck.
Gleichseitiges Dreieck		Man nagelt Anfang und Ende des Rechenseils zusammen. Für die Grundseite zählt man 5 ab. Für die Seiten darauf benötigt man jeweils 5 Knoten. Durch das Spannen dieser Seiten entsteht ein gleichseitiges Dreieck.
Kreis		Man nagelt ein Ende fest und befestigt einen Griffel an der gewünschten Stelle. Dann führt man den Griffel am gespannten Seil einmal herum.