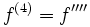- )
-
Satzzeichen -, –, —, ― . , , , ; , : , … , · ¿, ?, !, ¡, ‽, ؟ „…“, »…« …, ’ /, \ (…), […], {…}, 〈…〉 ␠ Sonstige Zeichen • … @, & |, ¦ °, ′, ″, ‴ *, ⁂, †, ‡ #, №, ª, º §, ¶ ©, ℗, ®, ™, ℠ _ ~, ˜ Rechenzeichen +, −, ×, ∙, :, ∕, ÷, ±, ∓ =, ≈, ≠ …, ~, ∝ …, <, > … √, ∫ %, ‰ Eine Klammer ist ein Zeichen oder Symbol, das zur Beschreibung einer Klammerung verwendet wird.
In der Schriftsprache dient sie als Satzzeichen zur Gliederung der syntaktischen Form. Eine großzügige Verwendung von Klammern gilt im deutschen Schriftsatz als schlechter Stil, Gedankenstriche oder die Auflösung von Schachtelsätzen werden meist bevorzugt. In anderen Sprachen, z. B. im Englischen, werden Klammern häufiger eingesetzt.
In der Mathematik drücken Klammern unter anderem einen Vorrang einer auszuführenden Rechenoperation vor anderen in der Rechenreihenfolge aus. Zum Beispiel ist das Ergebnis von 10 − (6 − 1) gleich 5, da die Rechnung innerhalb der Klammer zuerst ausgeführt wird, 10 − 6 − 1 ist dagegen gleich 3, da in diesem Fall von links nach rechts vorgegangen wird. In der höheren Mathematik dienen Klammern auch noch vielen anderen Zwecken, vor allem der Bezeichnung von Argumenten einer Funktion. Geschweifte, eckige und spitze Klammern haben in der Mathematik meist eine spezielle Bedeutung.
In ähnlicher Weise dienen Klammern auch in vielen Programmiersprachen zum Gruppieren von mehreren Arten von Programmelementen.
Inhaltsverzeichnis
Klammern in der Grammatik und Typographie
Gebräuchlich sind mehrere Arten von Klammern als Satzzeichen, welche fast ausschließlich paarig (also als öffnende und schließende Klammer) verwendet werden; die englischen Bezeichnungen unterscheiden sich im britischen (BE) und amerikanischen (AE) Englisch:
[]()- Runde Klammern: (…)
- (griechisch/engl.: parentheses [AE] oder round brackets [BE]): die üblichen Klammern
- Eckige Klammern: […]
- (engl.: brackets [AE] oder square brackets [BE]): Werden u. a. verwendet, wenn innerhalb eines Klammerausdrucks etwas geklammert werden soll oder um Auslassungen und Einfügungen in Zitaten kenntlich zu machen; Beispiele: „[AE]“ und „[BE]“ in diesem Absatz, „[sic]“ und „[…]“
〈〉{}- Geschweifte/Geschwungene Klammern (Akkoladen): {…}
- auch Mengenklammern oder Nasenklammern (engl.: braces [AE] oder curly brackets [BE], fr.: accolades) genannt: Werden selten verwendet, um mehrere Zeilen zusammenzufassen. Haben beispielsweise in Wörterbüchern eine spezielle Bedeutung.
- Spitze Klammern: 〈…〉
- Auch Winkelklammern (engl.: angle brackets) genannt. Werden nur selten verwendet. Haben in Wörterbüchern eine spezielle Bedeutung, etwa wird die (etymologische) Herkunft eines Wortes in spitze Klammern gesetzt, seltener auch Stilangaben in Wörterbüchern. Da diese Zeichen im ASCII-Zeichensatz fehlen, werden stattdessen oft die ASCII-Zeichen „Kleiner als“ < und „Größer als“ > benutzt.
Vor einer öffnenden und nach einer schließenden Klammer wird stets ein Leerzeichen gesetzt (außer es folgt – wie hier – ein Satzzeichen). Nach einer öffnenden und vor einer schließenden Klammer dagegen nicht.
【】〔〕〖〗〚〛Im Japanischen sind weitere Arten von Klammern gebräuchlich. Teilweise gibt es im Unicode-Zeichenstandard auch zusätzliche Kodierungen.
Klammern im Internationalen Phonetischen Alphabet
Eckige Klammern
[]Das Internationale Phonetische Alphabet (IPA) unterscheidet die Eckige Klammer links „[“ und die Eckige Klammer rechts „]“.
Im IPA geben die Zeichen „[“ und „]“ jeweils den Beginn bzw. das Ende der phonetischen Transkription an; sie besitzen die IPA-Nummern 901 bzw. 902.
Geschweifte/Geschwungene Klammern
{}Die geschweiften/geschwungenen Klammern im Internationalen Phonetischen Alphabet zeigen den Anfang bzw. das Ende prosodischer Notation an.
Klammern in der Mathematik
In der Mathematik werden Klammern meist ebenfalls paarig eingesetzt, wobei öffnende und schließende Klammer jeweils zueinander spiegelsymmetrisch sind. Es existieren jedoch Ausnahmen, etwa bei Intervallklammern, und auch einzelne, nicht paarige Klammern werden bisweilen verwendet.
Gruppierungsklammern in Termen
Klammern gruppieren Teilterme und verändern damit die Reihenfolge der Berechnung oder dienen lediglich der optischen Zusammenfassung von Teiltermen. Es werden hierfür üblicherweise runde Klammern verwendet. Bei komplexen Termen oder wenn spezielle Teilterme kenntlich gemacht werden sollen, können diese mit eckigen Klammern eingefasst werden.
Beispiel:
![\left[ (a+b)^2 - (a+c)^2 \right] ^ 2 - \left[ (a+b)^2 + (n^2-1) \right]^2](/pictures/dewiki/51/399b66fc56f12537c60fb309d498da85.png) statt
statt 
Mengenklammern
Bei Mengenangaben werden üblicherweise geschweifte Klammern benutzt:
Intervallklammern
Für Intervalle existieren verschiedene Notationen. Die beiden gebräuchlichsten sind im Falle eines offenen Intervalles
 und eines halboffenen Intervalles
und eines halboffenen Intervalles  :
:Statt eines Strichpunktes wird oft ein Komma zur Trennung der Intervallgrenzen verwendet, wenn eine Verwechslung mit dem Dezimalkomma ausgeschlossen ist.
Funktionsargumente
Gelegentlich werden Argumente von Funktionen in spitze statt in runde Klammern gesetzt, um eine bessere Unterscheidbarkeit von gruppierenden Klammern zu ermöglichen (f ist eine Funktion, g eine Variable):
 statt f(g + h) + g(h + j)
statt f(g + h) + g(h + j)Anzutreffen ist eine solche Schreibweise vor allem dort, wo in komplex geklammerten Termen verschiedene Funktionen auftauchen, etwa in der Statistik [1]:

UND-Klammern
Wenn mehrere Aussagen vertikal in einer großen geschweiften Klammer gruppiert werden, bedeutet dies, dass diese UND-verknüpft werden. Beispiel:
 ist gleichbedeutend mit
ist gleichbedeutend mit 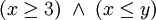 .
.Spezielle Operatoren
Andere ebenfalls paarig verwendete Klammern sind spezielle Operatoren oder Funktionen:
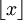 (manchmal auch [x]) bezeichnet die größte ganze Zahl kleiner oder gleich x („Gaußklammer“)
(manchmal auch [x]) bezeichnet die größte ganze Zahl kleiner oder gleich x („Gaußklammer“)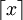 bezeichnet die kleinste ganze Zahl größer oder gleich x
bezeichnet die kleinste ganze Zahl größer oder gleich x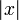 bezeichnet den Betrag von x
bezeichnet den Betrag von x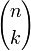 kann einen Binomialkoeffizienten bezeichnen (wenn n und k ganzzahlig sind und
kann einen Binomialkoeffizienten bezeichnen (wenn n und k ganzzahlig sind und 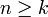 ) oder eine Matrix, und diese Matrix kann einen Vektor darstellen
) oder eine Matrix, und diese Matrix kann einen Vektor darstellen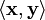 ist ein Skalarprodukt oder Cantorsche Paarungsfunktion; davon abgeleitet ist die Bra-Ket-Notation.
ist ein Skalarprodukt oder Cantorsche Paarungsfunktion; davon abgeleitet ist die Bra-Ket-Notation.![[\hat A, \hat B]=\hat A \hat B - \hat B \hat A](/pictures/dewiki/54/61ff7ed3006d4f448e5f621d05cd15a4.png) ist der Kommutator der zwei Operatoren
ist der Kommutator der zwei Operatoren 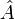 und
und 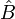 im mathematischen Formalismus der Quantenmechanik, wo auch
im mathematischen Formalismus der Quantenmechanik, wo auch![[\hat A,\hat B]_+=\hat A \hat B + \hat B \hat A](/pictures/dewiki/51/3918c780d14dfffbc280276e93626866.png) , der Antikommutator zweier Operatoren, definiert ist. Eine alternative Schreibweise hierfür ist
, der Antikommutator zweier Operatoren, definiert ist. Eine alternative Schreibweise hierfür ist  .
.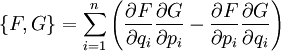 ist die Poissonklammer, ein bilinearer Differentialoperator in der hamiltonschen Mechanik.
ist die Poissonklammer, ein bilinearer Differentialoperator in der hamiltonschen Mechanik.![[F(x)]_a^b](/pictures/dewiki/97/a9d551c82bc4978566156d029a2d5933.png) ist die Kurzschreibweise des Integrals
ist die Kurzschreibweise des Integrals  , siehe auch Integralrechnung
, siehe auch Integralrechnung- (x)n,(x)n bezeichnet die fallende bzw. Faktorielle. aber: Verwechslungsgefahr mit dem Pochhammer-Symbol, das je nach Autor auch als x(n),
 oder (x,n) dargestellt wird.
oder (x,n) dargestellt wird.
Ableitungen
Höhere Ableitungen werden oft statt mit Ableitungsstrichen mit einem Exponenten in runden Klammern gekennzeichnet, da dies die Lesbarkeit erhöht:
Diese Notation wird ebenfalls verwendet, wenn die Anzahl der Ableitungen selbst über eine Variable oder einen Term ausgedrückt werden soll:
Klammern in Programmiersprachen
Klammern haben in verschiedenen Programmiersprachen unterschiedliche Bedeutungen. Bestimmte Bedeutungen sind jedoch relativ weit verbreitet:
- Runde Klammern
- Veränderung der Berechnungsreihenfolge in Termen (wie in der Mathematik)
- Funktionsargumente
- Typumwandlungs-Operator (z. B. in C und C++)
- Listenbildung (z. B. in LISP und verwandte Sprachen)
- Eckige Klammern
- Geschweifte Klammern (in der Informatik teilweise auch „geschwungene Klammern“)
- Blockgrenzen (z. B. in C, C++, Java, JavaScript, LilyPond)
- Array- und Struktur-Literale (C, C++, Java)
- Kommentare (Pascal)
- Spitze Klammern
- (Tatsächlich werden hier jedoch bisher ausschließlich die ASCII-Zeichen < und > verwendet)
Quellen
- ↑ Stahel, Werner A.: Statistische Datenanalyse. Eine Einführung für Naturwissenschaftler. 5. Auflage. Wiesbaden: Vieweg 2008.
Wikimedia Foundation.

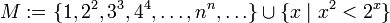
![A = \left] a;b \right[ \quad B = \left[ a;b \right[](/pictures/dewiki/53/52862f794d53891f2d895d2c9ca481f6.png)