Egalisator

Ein Differenzkern (auch: Egalisator) ist eine Verallgemeinerung des mathematischen Begriffes Kern auf beliebige Kategorien.

Der Differenzkern eines Paares von Abbildungen f, g zwischen zwei Mengen X und Y ist die Teilmenge von X, auf der f und g übereinstimmen, d.h.

ker(f, g) = { x ∈ X | f(x) = g(x) }.

Ein Differenzkern zweier Morphismen f, g: X → Y in einer beliebigen Kategorie ist das durch die folgenden äquivalenten Eigenschaften charakterisierte Unterobjekt i: ker(f,g) → X von X:

• Zu jedem Pfeil t: T → X, für den ft = gt gilt, gibt es genau einen Pfeil c: T→ ker(f,g), so dass t = ic.
• Hom(T,ker(f,g)) 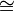$\cong$ ker(Hom(T,f),Hom(T,g)).

Beispiele

In den Kategorien der Gruppen, abelschen Gruppen, Vektorräume oder Ringe ist der Differenzkern zweier Morphismen der der zugrundeliegenden Mengenabbildungen.