- Elgamal-Verschlüsselungssystem
-
Das Elgamal-Kryptosystem (auch al-Dschamal-Kryptosystem) ist ein Schema zur Verschlüsselung, das auf dem mathematischen Problem des diskreten Logarithmus beruht. Elgamal ist ein asymmetrischer Verschlüsselungsalgorithmus aufbauend auf der Idee des Diffie-Hellman-Algorithmus, der mit diesen diskreten Logarithmen arbeitet.
Elgamal kann sowohl zur Signaturerzeugung als auch zum Verschlüsseln verwendet werden. Elgamal unterliegt keinem Patent.
Wie das Elliptische-Kurven-Kryptosystem basiert auch die Sicherheit des Elgamal-Kryptosystems auf der Annahme, dass diskrete Logarithmen eine Trapdoor-Einwegfunktion darstellen.
Inhaltsverzeichnis
Geschichte
Das Elgamal-Kryptosystem wurde 1985 von Taher Elgamal (Tahir al-Dschamal) entwickelt.
Schlüsselerzeugung
Wie alle asymmetrischen Kryptosysteme verwendet auch das Elgamal-Kryptosystem einen öffentlichen und einen geheimen Schlüssel. Der öffentliche dient später der Verschlüsselung und kann veröffentlicht werden, während der geheime nur den Empfängern der Nachricht bekannt sein darf.
Es folgt nun eine genaue mathematische Beschreibung der Schlüsselerzeugung:
Zur Schlüsselerzeugung benötigt man eine Primzahl p, sodass p − 1 einen großen Primfaktor q besitzt. Typischerweise wird q vorgewählt und man errechnet p = 2q + 1 und prüft dann die Primzahleigenschaft von p (Sophie-Germain-Primzahl). Außerdem benötigt man eine Primitivwurzel
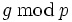 der Ordnung p − 1 und ein gleichverteilt zufälliges
der Ordnung p − 1 und ein gleichverteilt zufälliges 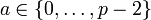 . Man berechne außerdem
. Man berechne außerdem 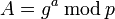 . Hierbei steht mod für den Modulo-Operator. Für eine Erläuterung solcher Kongruenzbedingungen siehe Modulo.
. Hierbei steht mod für den Modulo-Operator. Für eine Erläuterung solcher Kongruenzbedingungen siehe Modulo.Der öffentliche Schlüssel besteht nun aus dem Tripel (p,g,A). Der geheime Schlüssel entspricht a.
Seien beispielhaft p = 17 und a = 6. Als Primitivwurzel sei g = 3 gewählt. Man berechne
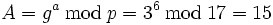 .
.Somit ergibt sich im Beispiel der öffentliche Schlüssel (p = 17,g = 3,A = 15) und der geheime Schlüssel a = 6.
Anmerkung
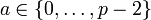 ist zwar möglich, hat aber sicherheitstechnisch keinen Sinn, da g0 = 1 und g1 = g, also wird vorzugsweise
ist zwar möglich, hat aber sicherheitstechnisch keinen Sinn, da g0 = 1 und g1 = g, also wird vorzugsweise 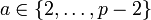 verwendet.
verwendet.Verschlüsselung
Man kann sich eine Verschlüsselung so vorstellen, dass ein Text, etwa aus einem Buch, durch ein geeignetes Verfahren in eine Zeichenfolge gewandelt wird, die nicht mehr ohne größeren Aufwand lesbar ist.
Nebenstehende Abbildung veranschaulicht die Verschlüsselung von Klartexten mit asymmetrischen Kryptosystemen wie dem in diesem Artikel beschriebenen. Ein Klartext wird in einen Geheimtext unter Verwendung eines öffentlichen Schlüssels verwandelt. Zur Handhabung im Rechner verwendet man jedoch eine Folge von Zahlen, in die sich ein solcher Textabschnitt jedoch leicht verwandeln lässt.
Für das Elgamal-Kryptosystem wird nachfolgend dieser Prozess auf mathematischem Weg präzisiert:
Der Klartext m ist aus der Menge
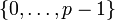 zu wählen. Man wähle nun zufällig ein
zu wählen. Man wähle nun zufällig ein 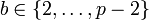 . Nun berechne man
. Nun berechne man 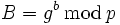 und
und 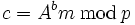 . Der Geheimtext besteht nun aus dem Paar (B,c).
. Der Geheimtext besteht nun aus dem Paar (B,c).In unserem Beispiel sei der Klartext m = 9. Willkürlich sei b = 5 gewählt. So berechne sich
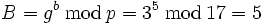 und
und 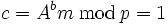 . Somit ergibt sich der Geheimtext (B = 5,c = 1).
. Somit ergibt sich der Geheimtext (B = 5,c = 1).Entschlüsselung
Auch die Entschlüsselung in asymmetrischen Kryptosystemen im Allgemeinen und im Elgamal-Kryptosystem im Speziellen ist nebenstehend in einer Abbildung dargestellt. Der zuvor durch Verschlüsselung entstandene Geheimtext wird unter Verwendung des geheimen Schlüssels wieder in den Klartext gewandelt.
Das genaue mathematische Vorgehen wird nun beschrieben:
Zur Entschlüsselung ist
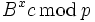 mit x = p − 1 − a zu berechnen. Dies lässt sich folgendermaßen veranschaulichen:
mit x = p − 1 − a zu berechnen. Dies lässt sich folgendermaßen veranschaulichen: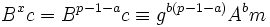
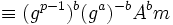
 (vgl. kleiner fermatscher Satz)
(vgl. kleiner fermatscher Satz) 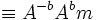
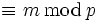 .
.Im Beispiel gilt
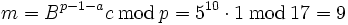 .
.oder einfach zum selber nachrechnen:
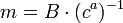 wobei mit hoch − 1 die multiplikative Inverse nach EEA gemeint ist.
wobei mit hoch − 1 die multiplikative Inverse nach EEA gemeint ist.Signatur
Signierung einer Nachricht
Anmerkung: H ist eine Hashfunktion ohne Kollisionen. Um eine Nachricht m zu signieren, sind vom Unterzeichner folgende Schritte zu vollführen:
- Bestimme eine Zufallszahl k, so dass 0 < k < p − 1 und ggT(k,p − 1) = 1.
- Berechne
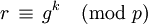 .
. - Berechne
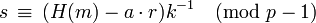
- Wenn s = 0, dann wiederhole die Schritte.
Das Paar (r,s) ist die digitale Signatur von m. Diese Schritte müssen vom Unterzeichner für jede Signatur wiederholt werden.
Verifikation einer signierten Nachricht
Eine Signatur (r,s) einer Nachricht m wird wie folgt verifiziert:
- 0 < r < p und 0 < s < p − 1.
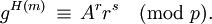
Der Empfänger der Nachricht akzeptiert die Signatur, falls diese Bedingungen zutreffen. Andernfalls muss er sie zurückweisen.
Bewertung
Effektivität
Momentan kann Elgamal als ein effektives Kryptosystem angesehen werden:
Wer diskrete Logarithmen berechnen kann, der kann Elgamal brechen („knacken“). Es gibt derzeit jedoch keine effizienten Algorithmen zur Berechnung diskreter Logarithmen, so dass sich diese – für genügend große Zahlen – nicht in „annehmbarer“ Zeit berechnen lassen. Deshalb wird heute davon ausgegangen, dass das Elgamal-Kryptosystem nicht in vertretbarer Zeit gebrochen und demnach als sicher eingestuft werden kann.
Wer nun das Diffie-Hellman-Problem lösen kann, der kann das Elgamal-Kryptosystem brechen. Wer das Elgamal-Kryptosystem brechen kann, der kann
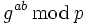 bestimmen.
bestimmen.Effizienz
Zur Verschlüsselung sind beim Elgamal-Kryptosystem zwei modulare Exponentiationen nötig:
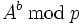 und
und 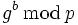 . Da diese nachrichtenunabhängig sind, sind sie vorberechenbar und abspeicherbar. Die Folge ist nur noch eine Multiplikation modulo p.
. Da diese nachrichtenunabhängig sind, sind sie vorberechenbar und abspeicherbar. Die Folge ist nur noch eine Multiplikation modulo p.Das Verfahren erfordert zur Entschlüsselung eine modulare Exponentiation. Im Gegensatz zum Rabin-Kryptosystem lässt es sich nicht mit dem chinesischen Restsatz beschleunigen.
Um jedoch Angriffe zu vermeiden, sollte immer ein neues b für jede neue Nachricht gewählt werden. So steigt zwar der Datenaufwand und die Anzahl der Verschlüsselungsschritte, jedoch ist es einem Angreifer nicht möglich, mit einem einmal gefundenem m alle vorherigen und nachfolgenden Nachrichten zu entschlüsseln. Dies hängt damit zusammen, dass sich
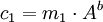 bei bekanntem m1 und c1 nach
bei bekanntem m1 und c1 nach 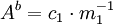 auflösen und ausrechnen lässt. Daraus folgt wiederum, dass
auflösen und ausrechnen lässt. Daraus folgt wiederum, dass 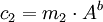 zu
zu 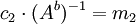 umgestellt werden kann und da c2 öffentlich ist, sich die Nachricht m2 bestimmen lässt. siehe Known Plaintext
umgestellt werden kann und da c2 öffentlich ist, sich die Nachricht m2 bestimmen lässt. siehe Known PlaintextLiteratur
- Johannes Buchmann: Einführung in die Kryptographie, 3., erweiterte Auflage. Springer, Berlin u. a. 2004, ISBN 3-540-40508-9
- Dietmar Wätjen: Kryptographie, 1. Auflage. Spektrum Akademischer Verlag, Heidelberg, 2004, ISBN 3-8274-1431-8
Wikimedia Foundation.

.png)
.png)