Erdős-Rényi-Graph

Ein Zufallsgraph bezeichnet einen Graphen, bei dem die Kanten zufällig erzeugt werden. Häufig eingesetzte Modelle zufälliger Graphen sind:

• Erdős-Rényi-Graph: G(n,p) mit einer natürlichen Zahl 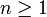$n \ge 1$ und einer Wahrscheinlichkeit 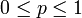$0 \le p \le 1$ bezeichnet die Menge aller Graphen, bei denen für jedes Tupel (v1,v2) von Knoten mit der Wahrscheinlichkeit p bestimmt wird, ob sie durch eine Kante verbunden werden, und das unabhängig von den anderen Kanten. Man untersucht dann häufig, mit welcher Wahrscheinlichkeit die erzeugten Graphen eine bestimmte Eigenschaft haben, z. B. ob sie zusammenhängend sind. Eine weitere Möglichkeit ist es, p = p(n) in Abhängigkeit von n vorzugeben und dann das Verhalten bei wachsendem n zu untersuchen.

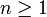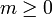• Das Modell G(n,m) mit natürlichen Zahlen $n \ge 1$ und $m \ge 0$ bezeichnet die Menge aller Graphen mit exakt n Knoten und m Kanten.

• Die Knoten V des Graphen G werden in der Ebene gemäß einer vorgegebenen Wahrscheinlichkeitsverteilung f verteilt. Wenn zwei Knoten v1,v2 einen Abstand kleiner als eine vorgegebene Grenze d haben, werden sie durch eine Kante verbunden.

Fragestellungen

Wichtige Fragestellungen bei zufälligen Graphen sind:

• Gegeben eine Eigenschaft Q und feste, für welche p bzw. m und ab welcher Graphengröße n besitzen alle Graphen die Eigenschaft Q?

• Gegeben eine Eigenschaft Q, geht die Wahrscheinlichkeit für Q gegen 1 oder 0 für 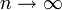$n \rightarrow \infty$? Man sagt dann auch, fast alle oder fast gar keine Graphen erfüllen die Eigenschaft Q.

Wichtige Ergebnisse

Einige NP-schweren Probleme lassen sich mit Hilfe zufälliger Graphen effizient beantworten. Beispielsweise kann Graph-Isomorphie für fast alle Graphen in O(n²) getestet werden. Auch für die Existenz von Cliquen existieren effiziente Ansätze, wenn die gesuchten Cliquen kleiner oder gleich 2lg(n) sind.

Literatur

• Douglas B. West: Introduction to Graph Theory, Prentice Hall, 1996, ISBN 0-13-227828-6