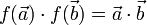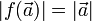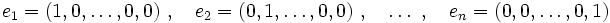Euklidvektorraum

Zunächst bezeichnet der Begriff euklidischer Raum den „Raum unserer Anschauung“ wie er in Euklids Elementen durch Axiome und Postulate beschrieben wird (vgl. euklidische Geometrie). Bis ins 19. Jahrhundert wurde als selbstverständlich davon ausgegangen, dass dadurch der uns umgebende physikalische Raum beschrieben wird. Der Zusatz „euklidisch“ wurde nötig, nachdem in der Mathematik allgemeinere Raumkonzepte (z. B. hyperbolischer Raum, riemannsche Mannigfaltigkeiten) entwickelt wurden und es sich im Rahmen der speziellen und allgemeinen Relativitätstheorie zeigte, dass zur Beschreibung des Raums in der Physik andere Raumbegriffe benötigt werden (Minkowski-Raum, Lorentz-Mannigfaltigkeit).

Im Laufe der Zeit wurde Euklids Geometrie auf verschiedene Arten präzisiert und verallgemeinert:

• axiomatisch durch Hilbert (vgl. Hilberts Axiomensystem der euklidischen Geometrie)
• als euklidischer Vektorraum (einem Vektorraum mit Skalarprodukt)
• als euklidischer Punktraum (einem affinem Raum, der über einem euklidischen Vektorraum modelliert ist)
• als Koordinatenraum 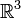$\R^3$ mit dem Standardskalarprodukt

Alle diese Präzisierungen sind gleichwertig. Wenn vom euklidischen Raum die Rede ist, dann kann jede von diesen gemeint sein oder auch eine höherdimensionale Verallgemeinerung. Den zweidimensionalen euklidischen Raum nennt man auch euklidische Ebene.

Vom affinen Raum unterscheidet sich der euklidische dadurch, dass man Längen und Winkel messen kann und demzufolge die Abbildungen auszeichnet, die Längen und Winkel erhalten. Diese nennt man traditionell Kongruenzabbildungen, andere Bezeichnungen sind Bewegungen und Isometrien.

Vom hyperbolischen Raum unterscheidet er sich dadurch, dass das Parallelenaxiom gilt.

Euklidische Vektorräume

Vom euklidischen Anschauungsraum zum euklidischen Vektorraum

In der analytischen Geometrie ordnet man dem euklidischen Raum einen Vektorraum zu. Eine Möglichkeit, dies zu tun, ist, die Menge der Parallelverschiebungen (Translationen) zu nehmen, versehen mit der Hintereinanderausführung als Addition. Jede Verschiebung lässt sich durch einen Pfeil beschreiben, der einen Punkt mit seinem Bildpunkt verbindet. Dabei beschreiben zwei Pfeile, die parallel sind und die gleiche Länge haben, dieselbe Verschiebung. Man nennt zwei solche Pfeile äquivalent und nennt die Äquivalenzklassen Vektoren. Nun kann man auch die Längen- und Winkelmessung aus dem euklidischen Raum auf Vektoren übertragen als Länge der zugehörigen Pfeile und Winkel zwischen solchen. Auf diese Art erhält man einen Vektorraum mit Skalarprodukt. 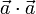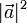Das Skalarprodukt ist dadurch charakterisiert, dass das Produkt $\vec a \cdot \vec a$ eines Vektors $\vec a$mit sich selbst das Quadrat $|\vec a|^2$ seiner Länge 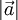$|\vec a|$ ergibt. 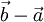Aus den Rechengesetzen für Skalarprodukte, den binomischen Formeln und dem Kosinussatz (angewandt auf ein Dreieck, dessen Seiten den Vektoren $\vec a$, $\vec b$ und $\vec b - \vec a$ entsprechen) ergibt sich die Formel

$\vec a \cdot \vec b = |\vec a| \, |\vec b| \,\cos \angle (\vec a, \vec b)$.

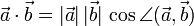Hierbei bezeichnet 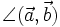$\angle (\vec a, \vec b)$ den Winkel zwischen den Vektoren $\vec a$ und $\vec b$.

Davon ausgehend nennt man jeden reellen Vektorraum mit Skalarprodukt einen euklidischen Vektorraum. Man benutzt dann obige Formel, um Länge (euklidische Norm) eines Vektors und Winkel zwischen Vektoren zu definieren. Zwei Vektoren sind dann orthogonal, wenn ihr Skalarprodukt null ergibt. Jeder drei-dimensionale euklidische Vektorraum ist isometrisch isomorph zum Vektorraum der Pfeilklassen und ebenso zum Koordinatenvektorraum 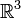$\R^3$ (siehe unten). Als euklidische Vektorräume sind diese also nicht unterscheidbar. Dies berechtigt einen, jeden solchen als den euklidischen Vektorraum zu bezeichnen.

Wählt man im euklidischen Raum einen Punkt O als Bezugspunkt (Ursprung) aus, so kann man jedem Punkt P seinen Ortsvektor 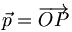$\vec p = \overrightarrow{OP}$ zuordnen, den Vektor, der durch einen Pfeil vom Ursprung O zum Punkt P dargestellt wird. Auf diese Art bekommt man eine Eins-zu-eins-Beziehung zwischen dem euklidischen Raum und dem zugehörigen euklidischen Vektorraum und kann so den ursprünglichen euklidischen Raum mit dem euklidischen Vektorraum identifizieren. Diese Identifizierung ist aber nicht kanonisch, sondern hängt von der Wahl des Ursprungs ab.

Orthonormalbasen

Sobald man einen reellen Vektorraum mit einem Skalarprodukt versehen hat, kann man die metrischen Begriffe des euklidischen Anschauungsraums auf diesen übertragen. Die Länge (Norm) eines Vektors $\vec a$ ist dann die Wurzel aus dem Skalarprodukt des Vektors mit sich selbst:

$|\vec a| = \sqrt{\vec a \cdot \vec a}$.

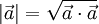Zwei Vektoren 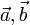$\vec a, \vec b$ sind orthogonal, wenn ihr Skalarprodukt null ist:

$\vec a \perp \vec b \Leftrightarrow \vec a \cdot \vec b = 0$.

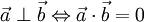Den (nichtorientierten) Winkel zwischen zwei Vektoren definiert man mittels der obigen Formel

$\vec a \cdot \vec b = |\vec a| \, |\vec b| \,\cos \angle (\vec a, \vec b)$,

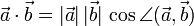also

$\angle (\vec a, \vec b) = \arccos \frac{\vec a \cdot \vec b}{|\vec a| \, |\vec b|}$.

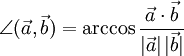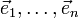Ein Vektor $\vec a$ heißt Einheitsvektor, wenn er die Länge 1 hat. Eine Basis aus Einheitsvektoren, die paarweise orthogonal sind, heißt Orthonormalbasis. In jedem euklidischen Vektorraum existieren Orthonormalbasen. Ist $\vec e_1, \dots, \vec e_n$ eine Orthonormalbasis, so lässt sich der Vektor $\vec a$ in dieser Basis darstellen:

$a = a_1 \vec e_1 + \cdots + a_n \vec e_n$.

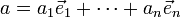Die Koeffizienten erhält man durch

$a_i = \vec a \cdot \vec e_i$.

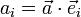Sind U und V zwei n-dimensionale euklidische Vektorräume, so nennt man eine lineare Abbildung 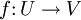$f \colon U \to V$ eine (lineare) Isometrie, wenn sie das Skalarprodukt erhält, wenn also gilt

$f(\vec a) \cdot f(\vec b) = \vec a \cdot \vec b$

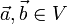für alle $\vec a, \vec b \in V$. Im Fall einer Selbstabbildung 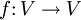$f \colon V \to V$ nennt man f eine orthogonale Abbildung. Eine Isometrie erhält insbesondere Längen

$|f(\vec a)| = |\vec a|$

und Winkel, also insbesondere Orthogonalität

$f(\vec a) \perp f(\vec b) \Longleftrightarrow \vec a \perp \vec b$.

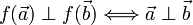Umgekehrt ist jede lineare Abbildung, die Längen erhält, eine Isometrie.

Eine Isometrie bildet jede Orthonormalbasis wieder auf eine Orthonormalbasis ab. Umgekehrt, wenn 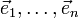$\vec e_1, \dots, \vec e_n$ eine Orthonormalbasis von V ist und 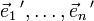$\vec e_1\,', \dots, \vec e_n\,'$ eine Orthonormalbasis von W, so gibt es genau eine Isometrie, die e_i auf e_i' abbildet.

Daraus ergibt sich, dass zwei euklidische Vektorräume derselben Dimension isometrisch sind, also als euklidische Vektorräume nicht unterscheidbar sind.

Der reelle Koordinatenraum

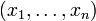Als den n-dimensionalen euklidischen Raum bezeichnet man auch oft den Koordinatenraum $\R^n$ mit dem Standardskalarprodukt. Die Punkte des Raumes sind n-Tupel $(x_1, \dots, x_n)$, das Skalarprodukt ist definiert durch

$(x_1, \dots, x_n) \cdot (y_1, \dots, y_n) = x_1 y_1 + \cdots + x_n y_n$.

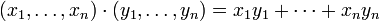Die Vektoren der Standardbasis

$e_1 = (1, 0, \dots, 0, 0)\ , \quad e_2 = (0,1,\dots,0, 0)\ , \quad \dots\ , \quad e_n = (0,0,\dots, 0, 1)$

sind Einheitsvektoren und paarweise orthogonal, bilden also eine Orthonormalbasis.

Algebraische Beschreibung

Indem man eine Orthonormalbasis wählt, lässt sich jeder beliebige euklidische Raum der Dimension n (n > 0) als das n-fache kartesische Produkt der reellen Zahlenmenge $\R$ beschreiben. Da bei dieser Beschreibung keine Informationen verlorengehen (die Räume sind isomorph und zwar so, dass das Skalarprodukt erhalten wird), wird der Begriff häufig auf diesen speziellen Raum eingeengt, der dann als $\R^n$ oder auch Eⁿ bezeichnet wird.

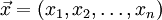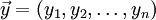Durch koordinatenweise Addition und Multiplikation mit Skalaren wird er zu einem reellen Vektorraum, auf dem für zwei beliebige Punkte $\vec x = (x_1, x_2, \ldots, x_n)$ und $\vec y = (y_1, y_2, \ldots, y_n)$ ein Skalarprodukt definiert werden kann, indem die Koordinaten paarweise multipliziert und die entstehenden Produkte aufaddiert werden. In drei Dimensionen ergibt sich so zum Beispiel

$\vec x \cdot \vec y=x_{1} y_{1}+x_{2} y_{2} +x_{3} y_{3}$.

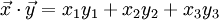Dieses Skalarprodukt, das sog. Standardskalarprodukt, ermöglicht die algebraische Definition von Abständen und Winkeln. Dazu wird zunächst für jeden Punkt x eine Norm genannte Länge festgelegt, die durch die Quadratwurzel aus dem Skalarprodukt des Vektors mit sich selbst definiert ist. Wiederum in drei Dimensionen ergibt sich zum Beispiel:

$\|\vec x\|=|\vec x|=\sqrt{\vec x\cdot \vec x}=\sqrt{(x_{1})^2+(x_{2})^2+(x_{3})^2}$.

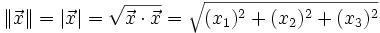Der Abstand zweier Punkte x und y ergibt sich nun durch die euklidische Metrik d(x,y) (euklidischer Abstand), die sich als Norm der Differenz x − y errechnet. Als Beispiel in drei Dimensionen gilt dann

$d(\vec x,\vec y)=|\vec x-\vec y|=\sqrt{(\vec x-\vec y)\cdot (\vec x-\vec y)}=\sqrt{(x_{1}-y_{1})^2+(x_{2}-y_{2})^2+(x_{3}-y_{3})^2}$.

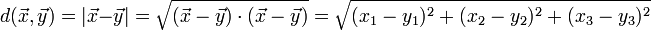Winkel zwischen zwei Vektoren x und y werden durch die Kosinus-Funktion festgelegt und zwar definiert sich der Kosinus des Winkels als Quotient aus dem Skalarprodukt von x,y und dem Produkt ihrer Normen

$\cos \alpha(\vec x,\vec y)=\frac{\vec x\cdot \vec y}{|\vec x || \vec y|}$.

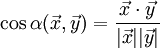Euklidische Räume als topologische Räume

Durch das Skalarprodukt wird eine Metrik und damit insbesondere eine Topologie auf dem $\R^n$ definiert. Als Vektorraum ist er zudem das klassische Beispiel für einen topologischen Vektorraum. Insbesondere ist er ein Prähilbertraum und, weil im endlichdimensionalen auch vollständig, ein Banachraum und somit auch ein Hilbertraum. Nach einem Beweis von Luitzen E. J. Brouwer sind euklidische Räume verschiedener Dimension nicht homöomorph aufeinander abbildbar.

Euklidische Räume als differenzierbare Mannigfaltigkeiten

Ein euklidischer Raum ist zugleich der Prototyp einer topologischen und differenzierbaren Mannigfaltigkeit. Für alle Dimensionen außer vier ist eine zu $\R^n$ homöomorphe differenzierbare Mannigfaltigkeit auch eine zu $\R^n$ diffeomorphe. Die in vier Dimensionen bestehenden Ausnahmen werden exotische 4-Räume genannt.

Euklidische Räume als geordnete Geometrie

Vergisst man die metrischen und topologischen Aspekte des $\R^n$, und denkt sich diese als System von Punkten, Strecken und Geraden, so erhält man eine geordnete Geometrie, nämlich die euklidische Geometrie. Charakteristisch für diese ist die Gültigkeit des Parallelenaxioms.

Euklidische Räume in der Differentialgeometrie

In der Differentialgeometrie bezeichnet das Wort euklidischer Raum eine riemannsche Mannigfaltigkeit, die isometrisch zum Vektorraum $\R^n$ mit dem Standard-Skalarprodukt als riemannscher Metrik ist. Für diese riemannschen Mannigfaltigkeiten verschwindet der Krümmungstensor, das heißt, der Raum ist flach. Umgekehrt ist jede flache riemannsche Mannigfaltigkeit lokal isometrisch zum $\R^n$ mit seiner Standard-Metrik. Es kann sich allerdings auch um eine offene Teilmenge eines $\R^n$ handeln oder um eine Mannigfaltigkeit, deren universelle Überlagerung eine Teilmenge des $\R^n$ ist. Zweidimensionale Beispiele für den letzten Fall sind ein flacher Torus oder ein gerader Kreiszylinder. Andererseits ist jede vollständige und einfach zusammenhängende flache riemannsche Mannigfaltigkeit ein euklidischer Raum.

Siehe auch

• Euklidische Geometrie
• Hierarchie mathematischer Strukturen

Weblinks

• Download von Rechnender Raum aus Elektronische Datenverarbeitung 8 (1967) 336-344 (pdf) von idsia.ch