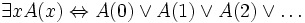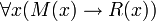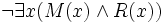Existenzoperator

Ein Quantor (auch: Quantifikator) ist ein Operator der Prädikatenlogik. Neben den Junktoren sind die Quantoren Grundzeichen der Prädikatenlogik. Allen Quantoren gemeinsam ist, dass sie Variablen binden.

Die beiden gebräuchlichsten Quantoren sind

• der „Existenzquantor“, auch Einsquantor, Existenzialquantifikator, Partikularisator, Singulärquantor^[1], Seinsquantor^[2]oder Manchquantor (z. B. "ein", "dieser", "jener")
• der „Allquantor“, auch Universalquantor, Universalquantifikator, universeller Quantor ^[3]oder Generalisator, genereller Quantor^[1](z. B. "alle", "alle diese")

Ferner gibt es:

• Nullklassenquantor^[1](z. B. "kein", "keine")
• Teilklassenquantor^[1](z. B. "manche", "diese")
• Anzahlquantor (z. B. "zwei", "drei")

Alle Quantoren außer dem Nullklassenquantor werden unterschieden in:

• determinierte Quantoren^[1](z. B. "ein", "manche")
• undeterminierte Quantoren^[1](z. B. "dieser", "diese")

Der Nullklassenquantor wird unterschieden in:

• singulare Nullklassenquantoren^[1]("kein")
• plurale Nullklassenquantoren^[1]("keine")

Existenz- und Allquantor

Schreib- und Sprechweise

Der Existenzquantor wird durch das Zeichen ∃ (ein horizontal gespiegeltes „E“) oder durch das Zeichen 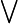$\bigvee$ dargestellt, manchmal (vor allem in maschinegeschriebenen Texten) als geklammertes gewöhnliches „E“. Der Allquantor wird durch das Zeichen ∀ (ein vertikal gespiegeltes „A“) oder das Zeichen 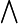$\bigwedge$ oder einfach durch eine in Klammern gesetzte Variable dargestellt.

Schreibweise	Variante 1	Variante 2	Sprechweise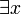
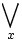
$\exists x$	$\bigvee_{x}$	(Ex)	Für (mindestens) ein/einige/manche x gilt; Es existiert/gibt ein x, für das gilt
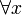
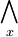
$\forall x$	$\bigwedge_{x}$	(x)	Für alle/jedes x gilt

Die Schreibweise 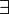$\exists$ (nicht den Existenzquantor selber) führte Giuseppe Peano 1897 im ersten Band seines Formulaire de mathématiques ein;^[4] verbreitet wurde sie durch ihre Verwendung in den Principia Mathematica, dem ab 1910 erschienenen Grundlagenwerk Russells und Whiteheads. Die Schreibweise 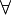$\forall$ (nicht den Allquantor selbst) führte Gerhard Gentzen 1934 ein.

Wahrheitsbedingungen

Die Aussage 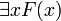$\exists x F(x)$ ist wahr, wenn es mindestens ein x gibt, das die Eigenschaft F hat. Die Aussage ist also auch dann wahr, wenn alle x F sind. Die Aussage 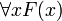$\forall x F(x)$ ist wahr, wenn alle x F sind, sonst falsch.

Es erscheint naheliegend, den Existenzquantor als Verkettung von Disjunktionen („oder“) und den Allquantor als Verkettung von Konjunktionen („und“) aufzufassen. Gehen wir davon aus, dass x als Wert eine natürliche Zahl annehmen kann, so ist man versucht zu schreiben:

$\exists x A(x) \Leftrightarrow A(0) \lor A(1) \lor A(2) \lor \dots$

$\forall x A(x) \Leftrightarrow A(0) \land A(1) \land A(2) \land \dots$

Der entscheidende Unterschied ist aber, dass die Variable des Quantors bei unendlich großem Individuenbereich potentiell unendlich viele Werte annehmen kann, während eine Konjunktion oder Disjunktion niemals unendlich lang werden kann. Daher muss man sich bei obigem Beispiel auch am Ende der Konjunktion bzw. Disjunktion mit Punkten (für „usw.“) behelfen.

Beispiele für Formalisierungen

Beispiele für einstellige Prädikate

Wenn die Leerstelle eines einstelligen Prädikats durch einen Quantor gebunden wird, entsteht bereits eine fertige Aussage. Es gibt daher nur zwei Möglichkeiten, ein einstelliges Prädikat mittels eines Quantors in eine Aussage zu überführen: Allquantifizierung und Existenzquantifizierung.

Am Beispiel des einstelligen Prädikats „_ ist rosa“, das hier als „F(_)“ formalisiert werden soll:

Allquantifizierung

„Alles ist rosa“ – „Für jedes Ding gilt, dass es rosa ist“ – „Für jedes x gilt: x ist rosa“. $\forall x F (x)$

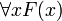
Existenzquantifizierung

„Etwas (mindestens ein ‚Ding‘) ist rosa“ – „Es gibt mindestens ein ‚Ding‘, das rosa ist“ – „Es gibt mindestens ein x, für das gilt: x ist rosa“. $\exists x F (x)$

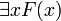
Beispiele für komplexe Sätze

Beim Formalisieren sprachlicher Äußerungen verbindet sich der Existenzquantor auf natürliche Weise mit dem „und“ (Konjunktion) und der Allquantor mit dem „wenn–dann“ (materiale Implikation)

Wollen wir den Satz formalisieren:

Ein Mann raucht.

so ist dieser zunächst aufzufassen als:

Es gibt jemanden, der Mann ist und raucht.

beziehungsweise – wenn man, wie in der Formalisierung, die Koreferenz des relativen Anschlusses „jemand ... der“ durch die Verwendung einer Variable ausdrückt –:

Es gibt mindestens ein x, für das gilt: x ist ein Mann und x raucht.

(man beachte das „und“) und dann folgendermaßen zu formalisieren:

$\exists x (M(x) \land R(x))$,

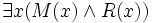wobei M(x) für „x ist Mann“ und R(x) für „x raucht“ steht.

Formalisieren wir dagegen:

Alle Männer rauchen.

so formen wir dies zunächst um in:

Für jedes „Ding“ gilt: Wenn es ein Mann ist, dann raucht es.

beziehungsweise:

Für jedes x gilt: Wenn x ein Mann ist, dann raucht x.

(wo wir das „wenn–dann“ verwenden) und formalisieren dann:

$\forall x (M(x) \rightarrow R(x))$

Der natürlichsprachliche Quantor „kein“ lässt sich auf verschiedene Weisen formalisieren:

Kein Mann raucht.

lässt sich umschreiben als:

Es stimmt nicht, dass es mindestens ein „Ding“ gibt, das Mann ist und das raucht.

beziehungsweise:

Es stimmt nicht, dass es mindestens ein x gibt, für das gilt: x ist ein Mann und x raucht.

worauf man es wie folgt formalisieren kann:

$\lnot \exists x (M(x) \land R(x))$

Eine andere Formalisierung erreicht man, wenn man die Aussage „Kein Mann raucht“ auffasst als „Für alle x gilt: wenn x ein Mann ist, raucht x nicht“.

Beispiele für quantorenlogische Satzformeln

Einfach quantifizierte Satzformeln

$\forall x (S(x) \rightarrow R(x) )$

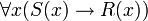
Für alle Dinge x gilt: wenn das Prädikat S auf x zutrifft, so trifft auch das Prädikat R auf x zu. Oder: Alle S sind R.

$\forall x (S(x) \rightarrow \lnot R(x) )$

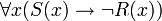
Für alle Dinge x gilt: wenn das Prädikat S auf x zutrifft, so trifft das Prädikat R auf x nicht zu. Oder: Alle S sind nicht R. Oder: Kein S ist ein R.

$\exists x (S(x) \wedge R(x) )$

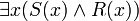
Es gibt (mindestens) ein Ding x, für das gilt: das Prädikat S trifft auf x zu und das Prädikat R trifft auf x zu. Oder: Einige S sind R.

$\exists x (S(x) \wedge \lnot R(x) )$

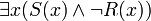
Es gibt (mindestens) ein Ding x, für das gilt: das Prädikat S trifft auf x zu und das Prädikat R trifft auf x nicht zu. Oder: Einige S sind nicht R.

$\forall x (S(x) \wedge R(x) )$

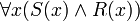
Für alle Dinge x gilt: das Prädikat S trifft auf x zu und das Prädikat R trifft auf x zu. Oder: Alles ist S und R.

$\exists x (S(x) \rightarrow R(x) )$

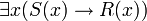
Es gibt (mindestens) ein Ding x, für das gilt: wenn das Prädikat S auf x zutrifft, so trifft das Prädikat R auf x zu. Oder: Nicht alle x sind nicht (S und R).

$\forall x ( Schwein(x) \rightarrow Rosa(x) )$

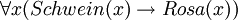
Alle Schweine sind rosa (wörtlich: Für jedes Ding gilt: Wenn es ein Schwein ist, dann ist es auch rosa.)

$\forall x ( Schwein(x) \rightarrow \lnot Rosa(x) )$

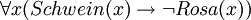
Kein Schwein ist rosa (wörtlich: Für jedes Ding gilt: Wenn es ein Schwein ist, dann ist es nicht rosa.)

$\exists x( Schwein(x) \wedge Rosa(x) )$

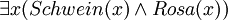
Es gibt mindestens ein rosa Schwein (wörtlich: Es gibt mindestens ein Ding, das sowohl Schwein als auch rosa ist.)

$\exists x( Schwein(x) \wedge \lnot Rosa(x) )$

Es gibt mindestens ein nichtrosa Schwein (wörtlich: Es gibt mindestens ein Ding, das sowohl Schwein als auch nichtrosa ist.)

$\forall x ( Schwein(x) \wedge Rosa(x) )$

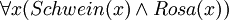
Alles ist ein rosa Schwein (wörtlich: Für jedes Ding gilt, dass es sowohl ein Schwein als auch rosa ist).

$\exists x ( Schwein(x) \rightarrow Rosa(x) )$

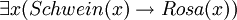
Diese selten gebrauchte Aussage, deren wörtliche Übersetzung „Es gibt mindestens ein Ding, das unter der Voraussetzung, dass es ein Schwein ist, auch rosa ist“ lautet, trifft die Feststellung, dass nicht alle Dinge nichtrosa Schweine sind.

Mehrfach quantifizierte Satzformeln

$\exists x \exists y Liebt(x,y)$

$\exists y \exists x Liebt(x,y)$

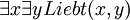
Die beiden Aussagen „Mindestens eine/r liebt mindestens eine/n“ und „Mindestens eine/r wird von mindestens einer/m geliebt“ sind synonym.

$\forall x \forall y Liebt(x,y)$

$\forall y \forall x Liebt(x,y)$

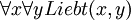
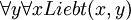
Die beiden Aussagen „Jede/r liebt jede/n“ und „Jede/r wird von jeder/m geliebt“ sind synonym.

$\exists x \forall y Liebt(x,y)$

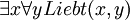
Es gibt jemanden, der/die alle liebt (wörtlich: Es gibt ein Ding, sodass für alle Dinge gilt, dass ersteres letzteres liebt); kürzer: Jemand liebt alle.

$\exists y \forall x Liebt(x,y)$

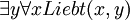
Es gibt jemanden, der/die von allen geliebt wird (wörtlich: Es gibt ein Ding, sodass für alle Dinge gilt, dass letzteres ersteres liebt); kürzer: Jemand wird von allen geliebt (d. h. alle lieben denselben bzw. dieselbe/n).

$\forall x \exists y Liebt(x,y)$

Für jeden gibt es jemanden, sodass erstere/r letztere/n liebt (wörtlich: Für jedes Ding gibt es ein Ding, sodass ersteres letzteres liebt), kürzer: Jede/r liebt irgendjemanden (d. h. jeder liebt, aber es muss nicht jeder denselben/dieselbe/n lieben).

$\forall y \exists x Liebt(x,y)$

Für jede/n gibt es jemanden, der/die ihn oder sie liebt (wörtlich: Für jedes Ding gibt es ein Ding, sodass letzteres ersteres liebt); kürzer: Niemand ist ungeliebt.

Komplexe Beispiele

$\exists x(F(x) \wedge \forall y (F(y) \rightarrow x=y))$

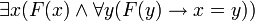
„Es gibt genau ein F,“ wörtlicher: „Es gibt mindestens ein ‚Ding‘, das einerseits F ist und für das gilt, dass alle ‚anderen‘ F mit diesem identisch sind.“

$\exists xF(x) \wedge \forall x \forall y ((F(x)\wedge F(y))\rightarrow x=y)$

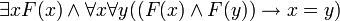
Ein Synonym zum vorgenannten Satz, wörtlich: „Es gibt mindestens ein F, und für alle ‚Dinge‘ x und alle ‚Dinge‘ y gilt: Wenn sowohl x als auch y F sind, dann sind x und y identisch.“

Wechselseitige Definierbarkeit der Quantoren

In der klassischen Logik lässt sich jeder der beiden Quantoren durch den jeweils anderen ausdrücken:

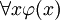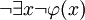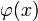1. Die Allaussage $\forall x \varphi(x)$ („alle x sind $\varphi$“) ist äquivalent mit einer verneinten Existenzaussage, $\lnot \exists x \lnot \varphi(x)$ („es gibt kein x, das nicht $\varphi$ ist“); dabei ist $\varphi(x)$ eine Aussageform, in der die Variable x frei vorkommen darf, aber nicht muss.
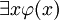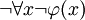2. Die Existenzaussage $\exists x\varphi(x)$ („mindestens ein x ist $\varphi$“) ist äquivalent mit einer verneinten Allaussage, $\lnot \forall x \lnot\varphi(x)$ („Es ist nicht der Fall, dass alle x nicht $\varphi$ sind“).

Auf Grund obiger Äquivalenzen kann man sich damit begnügen, in einer formalen Sprache für die klassische Prädikatenlogik nur einen der beiden Quantoren als Grundzeichen zu verwenden und den anderen Quantor gegebenenfalls durch diesen zu definieren.

Beispiel für (1)

Wenn alles vergänglich ist, so ist nichts unvergänglich. Umgekehrt: Ist nichts unvergänglich, so sind alle Dinge vergänglich.

Beispiel für (2)

Wenn es etwas Grünes gibt, so sind nicht alle Dinge nicht grün. Umgekehrt: Sind nicht alle Dinge nicht grün, muss es etwas Grünes geben.

Moderne Quantoren und aristotelische Syllogistik

Bei der Formalisierung einer Allaussage ist zu beachten, dass gemäß den Bedeutungsfestlegungen von Allquantor und Implikation eine Aussage „Für alle x: Wenn A(x), dann B(x)“ bereits wahr ist, wenn es keine A gibt. Demnach ist also beispielsweise die Aussage:

Alle eckigen Kreise sind golden.

wahr, weil es keine eckigen Kreise gibt.

Dies führt dazu, dass manche Schlussfolgerungen der aristotelischen Syllogistik nicht gültig sind, wenn man deren Allaussagen mit den modernen Quantoren identifiziert.

Als Beispiel sei der so genannte Modus Barbari aufgeführt:

Alle Münchner sind Bayern, (Formalschreibweise mit Quantoren: $\forall x ( M(x) \supset B(x) )$)

alle Schwabinger sind Münchner, (formal: $\forall x ( S(x) \supset M(x) )$) es folgt:

einige Schwabinger sind Bayern. (formal: $\exists x ( S(x) \land B(x) )$)

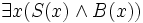Nach moderner Auffassung wären die Prämissen beide wahr, wenn es überhaupt keine Schwabinger und Münchner gäbe. Dann wäre aber die Konklusion falsch: Da es keine Schwabinger gäbe, könnten dann auch nicht einige Schwabinger Bayern sein. Die Prämissen könnten also wahr sein und die Konklusion dennoch falsch, d. h. es handelte sich nicht um einen gültigen Schluss. Aristoteles hat wohl bei einer Aussage „Alle A sind B“ immer die Existenz von As vorausgesetzt, sodass die einfache Übersetzung $\forall x ( M(x) \supset B(x) )$ seinen Absichten nicht gerecht wird. Welches die adäquate Interpretation und Übersetzung der syllogistischen Allaussagen ist, ist bis heute Gegenstand der Forschung; Informationen und Literaturhinweise gibt der Artikel Syllogismus.

Auch bei der einfachen Übersetzung als allquantifizierte Implikation gültig ist jedoch beispielsweise der so genannte Modus Barbara, nach dem aus den obigen Prämissen folgt:

Alle Schwabinger sind Bayern (formal: $\forall x ( S(x) \supset B(x) )$).

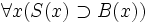Diese Aussage folgt, weil sie nach moderner Auffassung auch dann wahr wäre, wenn es gar keine Schwabinger gäbe

Anzahlquantoren

Neben All- und Existenzquantor werden in der Logik gelegentlich Anzahlquantoren gebraucht. So lässt sich ausdrücken, dass es „genau ein“, „genau zwei“, ... Dinge gibt, für die irgend etwas gilt.

Im Unterschied zum Existenzquantor, der besagt, dass es mindestens ein x gibt, für das etwas gilt, bedeutet der „Einzigkeitsquantor“, dass es genau ein solches x gibt (nicht mehr und nicht weniger). Für ihn schreibt man 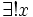$\exists! x$. Man kann diesen Quantor vermittels dem All- und dem Existenzquantor sowie dem Identitätszeichen „=“ wie folgt definieren:

$\exists! x B(x) = \exists x \bigl(B(x) \land \forall y\ (B(y) \rightarrow y=x)\bigr)$,

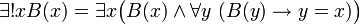in Worten:

„Es gibt genau ein x, für das B(x) gilt, ist gleichbedeutend damit, dass ein x existiert, für das B(x) gilt und für alle y gilt: wenn B(y) gilt, dann ist y identisch mit x.“

Allgemein lassen sich analog zum Einzigkeitsquantor für 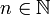$n \in \mathbb N$ auch Quantoren 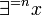$\exists^{=n} x$ definieren, die besagen, dass es genau n verschiedene x gibt. Insbesondere ist 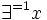$\exists^{=1} x$ äquivalent zu $\exists! x$.

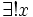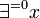$\exists^{=0} x$ definiert man entsprechend als 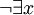$\lnot \exists x$, wofür manchmal auch der Quantor $\nexists$ benutzt wird: „Es gibt kein x mit ....“

Weitere Quantoren, wie z.B. „die meisten x“ werden in der Logik nur selten behandelt.

Siehe auch

• Quantorenunverträglichkeit

Quellen

1. ↑ ^{a b c d e f g h} Klaus A. Schneewind:Methodisches Denken in der Psychologie, Verlag Hans Huber, Stuttgart 1969, S. 74-78
2. ↑ http://www.phillex.de/exquant.htm
3. ↑ http://www.phillex.de/allquant.htm
4. ↑ Florian Cajori: A History of Mathematical Notations. Volume II: Notations Mainly in Higher Mathematics. Open Court Chicago 1929, nachgedruckt als ein Band bei Dover, ISBN 0-486-67766-4