Fachverteilung

Radixsort (von lat. Wurzel, Basis) oder auch Distributionsort (von engl. Distribution – „Verteilung“), oder im Deutschen Fachverteilen, ist ein lineares, stabiles Sortierverfahren, das out-of-place arbeitet und auf Countingsort basiert. Das Sortierverfahren hat unter der Voraussetzung, dass die maximale Länge der zu sortierenden Schlüssel von vornherein bekannt ist, lineare Laufzeit (abhängig von der Anzahl der Elemente, die zu sortieren sind).

Voraussetzungen

Bei Radixsort wird davon ausgegangen, dass die Schlüssel der zu sortierenden Daten nur aus Zeichen eines endlichen Alphabets bestehen. Zusätzlich muss eine Totalordnung zwischen den Zeichen des Alphabets bestehen.

Eine zweite Voraussetzung ist, dass die Länge der Schlüssel durch eine (von vornherein bekannte) Konstante begrenzt ist, da die Anzahl der Stellen pro Schlüssel eine entscheidende Auswirkung auf die Linearität des Laufzeitverhaltens hat.

Vorgehensweise

Radixsort besteht aus zwei Phasen, die immer wieder abwechselnd durchgeführt werden. Die Partitionierungsphase dient dazu, die Daten auf Fächer aufzuteilen, während in der Sammelphase die Daten aus diesen Fächern wieder aufgesammelt werden. Beide Phasen werden für jede Stelle der (zu sortierenden) Schlüssel einmal durchgeführt.

Partitionierungsphase 

In dieser Phase werden die Daten in die vorhandenen Fächer aufgeteilt, wobei für jedes Zeichen des zugrundeliegenden Alphabets ein Fach zur Verfügung steht. In welches Fach der gerade betrachtete Schlüssel gelegt wird, wird durch das an der gerade betrachteten Stelle stehende Zeichen bestimmt. So wird zum Beispiel die Zahl 352 in das Fach 3 gelegt, wenn gerade die dritte Stelle (von hinten) betrachtet wird.

Sammelphase 

Nach der Aufteilung der Daten in Fächer in Phase 1 werden die Daten wieder eingesammelt und auf einen Stapel gelegt. Hierbei wird so vorgegangen, dass zuerst alle Daten aus dem Fach mit der niedrigsten Wertigkeit eingesammelt werden, wobei die Reihenfolge der darin befindlichen Elemente nicht verändert werden darf. Danach werden die Elemente des nächst höheren Faches eingesammelt und an die schon aufgesammelten Elemente angefügt. Dies führt man fort bis alle Fächer wieder geleert wurden.

Diese beiden Phasen werden nun für jede Stelle der Schlüssel wiederholt, wobei mit der letzten Stelle begonnen wird und in der letzten Iteration die erste Stelle zum Aufteilen verwendet wird. Nach dem Aufsammeln für die erste Stelle der Schlüssel sind die Daten aufsteigend sortiert.

Beispiel

Es sollen folgende Zahlen geordnet werden:

124, 523, 483, 128, 923, 584

Zunächst wird nach der letzten Stelle geordnet.

Es beginnt die Partitionierungsphase:

|0| |1| |2| |3| |4| |5| |6| |7| |8| |9|
             |   |               |
            523 124             128
            483 584 
            923

Es folgt die Sammelphase (Elemente von links nach rechts, von oben nach unten aufsammeln):

523, 483, 923, 124, 584, 128

Nun nach der mittleren Stelle (im Allgemeinen von rechts nach links jeweils eine Stelle weiter).

Erneute Partitionierungsphase:

|0| |1| |2| |3| |4| |5| |6| |7| |8| |9|
         |                       |
        523                     483
        923                     584
        124
        128

Nun eine zweite Sammelphase:

523, 923, 124, 128, 483, 584

Und jetzt wird nach der ersten Stelle geordnet.

Die letzte Partitionierungsphase:

|0| |1| |2| |3| |4| |5| |6| |7| |8| |9|
     |           |   |               |
    124         483 523             923
    128             584

Es folgt die letzte Sammelphase:

124, 128, 483, 523, 584, 923

Die Zahlen sind nun aufsteigend sortiert.

Implementierung

Funktion zum Sortieren von Feldern mit Binaerzahlen implementiert mit Pseudocode.

Vorbedingung:
    a = Feld mit Binaerzahlen mit je k Stellen
    n = Laenge des Feldes

Algorithmus:
    Setze i = k - 1

    Solange i >= 0

        Setze L = 0
        Setze R = n - 1

        Solange L < R
            swap(a, L, R) // Tauscht Position L und R in a

            Solange a[L].bit(i) = 0 Und L < R
                Setze L = L + 1

            Solange a[R].bit(i) = 1 Und R > L
                Setze R = R - 1

        Setze i = i -1

Nachbedingung:
    a ist jetzt Permutation vom urspruenglichen Feld

Laufzeit

Die Laufzeit des Algorithmus lässt sich durch 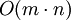$O(m \cdot n)$ abschätzen, wobei m die maximale Länge eines Schlüssels und n die Anzahl der zu sortierenden Elemente bezeichnen. Nimmt man nun an, dass m konstant ist, folgt daraus, dass dieses Sortierverfahren linear ist.

Siehe auch

• Bucketsort

Weblinks

• Radixsort auf linux-related.de
• Radixsort auf stefan-baur.de
• Extrem schnelle C++ Implementierung von Radixsort für Gleitkommazahlen