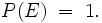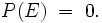Fast sichere Eigenschaften — Fast sicher ist ein Begriff der Wahrscheinlichkeitstheorie und äquivalent zu dem Begriff fast überall aus der Maßtheorie. Definition In einem Wahrscheinlichkeitsraum (Ω,Σ,P) heißt ein Ereignis fast sicher, wenn es mit Wahrscheinlichkeit eins… … Deutsch Wikipedia
Fast unmöglich — Fast sicher ist ein Begriff der Wahrscheinlichkeitstheorie und äquivalent zu dem Begriff fast überall aus der Maßtheorie. In einem Wahrscheinlichkeitsraum (Ω,Σ,P) heißt ein Ereignis fast sicher, wenn es mit Wahrscheinlichkeit eins eintritt, das… … Deutsch Wikipedia
Fast sichere Konvergenz — In der Stochastik existieren verschiedene Konzepte eines Grenzwertbegriffs für Zufallsvariablen. Anders als im Fall reeller Zahlenfolgen gibt es keine natürliche Definition für das Grenzverhalten von Zufallsvariablen bei wachsendem… … Deutsch Wikipedia
Fast Ethernet — In diesem Artikel oder Abschnitt fehlen folgende wichtige Informationen: Metro Ethernet. Du kannst Wikipedia helfen, indem du sie recherchierst und einfügst … Deutsch Wikipedia
sicher — sị·cher Adj; 1 vor Gefahren oder Risiken geschützt ↔ unsicher <ein Versteck, ein Weg; ein Arbeitsplatz, ein Einkommen; irgendwo sicher sein; sich irgendwo sicher fühlen; etwas aus sicherer Entfernung beobachten> 2 so, dass Fehler oder… … Langenscheidt Großwörterbuch Deutsch als Fremdsprache
Fast Etherchannel — Die Artikel Etherchannel, Link Aggregation, Bündelung und Bündel (Nachrichtentechnik) überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese… … Deutsch Wikipedia
Populäre Musik - Musik, die \(fast\) alle hören — Ob wir in der Disco, beim Jazzabend oder im Neue Musik Konzert in der Kunsthalle mit anderen Menschen ein Publikum bilden stets kommt es zu einer partiellen Identität von Orten, Inhalten und Personen. Der Rocker ist eher selten im… … Universal-Lexikon
Gesetze des iterierten Logarithmus — Als Gesetz des iterierten Logarithmus werden mehrere Grenzwertsätze aus der Wahrscheinlichkeitstheorie bezeichnet. Sie treffen Aussagen über das asymptotische Verhalten von Summen von Zufallsvariablen beziehungsweise von stochastischen Prozessen … Deutsch Wikipedia
Brownian motion — Zwei unabhängige Standard Wiener Prozesse Ein Wiener Prozess ist ein zeitstetiger stochastischer Prozess, der normalverteilte, unabhängige Zuwächse hat. Benannt wurde der Prozess, der auch als Brownsche Bewegung bekannt ist, nach dem… … Deutsch Wikipedia
Wiener-Prozess — Zwei Beispielpfade eines Standard Wiener Prozesses Ein Wiener Prozess ist ein zeitstetiger stochastischer Prozess, der normalverteilte, unabhängige Zuwächse hat. Benannt wurde der Prozess, der auch als Brownsche Bewegung bekannt ist, nach dem… … Deutsch Wikipedia
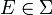 fast sicher, wenn es mit Wahrscheinlichkeit eins eintritt, das heißt wenn
fast sicher, wenn es mit Wahrscheinlichkeit eins eintritt, das heißt wenn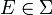 fast unmöglich, wenn
fast unmöglich, wenn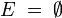 ist auch fast unmöglich.
ist auch fast unmöglich.![[0,1]\in\mathbb R](/pictures/dewiki/57/9df226930b52825f621bbcf48daaf283.png) genau eine bestimmte Zahl zufällig zu treffen, ist 0, obwohl dieses Ereignis nicht unmöglich ist. Entsprechend ist die Wahrscheinlichkeit, das Intervall außer einer bestimmten Zahl zu treffen, gleich 1, aber dieses Ereignis wird nicht mit Sicherheit eintreten.
genau eine bestimmte Zahl zufällig zu treffen, ist 0, obwohl dieses Ereignis nicht unmöglich ist. Entsprechend ist die Wahrscheinlichkeit, das Intervall außer einer bestimmten Zahl zu treffen, gleich 1, aber dieses Ereignis wird nicht mit Sicherheit eintreten.