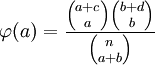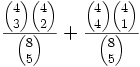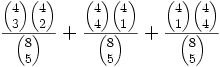Fischer-Test

Der Exakte Fisher-Test ist ein Signifikanztest auf Unabhängigkeit in der Kontingenztafel, welcher auch bei einer geringen Anzahl von Beobachtungen zuverlässige Resultate liefert. Im Anwendungsgebiet entspricht er dem Chi-Quadrat-Test. Er geht auf den britischen Statistiker Ronald Aylmer Fisher (1890-1962) zurück.

Chi-Quadrat-Tests funktionieren als asymptotische Tests und sind deshalb erst ab einer bestimmten Stichprobengröße zuverlässig. Im Falle der Kontingenztafeln gilt als Faustregel, dass pro Feld einer Kontigenztafel mindestens etwa fünf Beobachtungen erwartet werden und dass mehr als ein Freiheitsgrad vorhanden ist. Ein Untersuchungsergebnis wie zum Beispiel

	A	not A	$\sum$
B	a	b	a+b
not B	c	d	c+d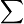
$\sum$	a+c	b+d	n=a+b+c+d

$\varphi (a) = \frac{{a + c \choose a}{b +d \choose b}}{{n \choose a + b}}$

In anderer Schreibweise (Bortz,Lienert,Boehnke 1990) 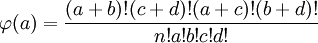$\varphi (a) = \frac{{(a + b)!}{(c +d)!}{(a + c)!}{(b +d)!}}{{n!}{a!b!c!d!}}$ auch für kxl erweiterbar.

Beispiel

Leistungen von Schülern einer kleinen Klasse	männlich	weiblich
genügend	3	1
ungenügend	2	2

kann mit dem Chi-Quadrat-Test bzw. dem Vierfeldertest daher nur schlecht auf seine statistische Signifikanz geprüft werden. Der exakte Test von Fisher hält dagegen auch bei wenigen Beobachtungen das geforderte Niveau.

Der exakte Test bildet Kombinationen von Zellhäufigkeiten, die bei festen Zeilen- und Spaltensummen entstehen könnten, und berechnet die bedingte Wahrscheinlichkeit für die Zellhäufigkeiten, gegeben die Randsummen. Es werden die Wahrscheinlichkeiten für den vorgegebenem Fall und für die extremeren Fälle berechnet und addiert. Diese Wahrscheinlichkeiten folgen, wenn die Nullhypothese stimmt, einer hypergeometrischen Verteilung. In den Ablehnbereich werden zunächst die Kombinationen von Zellhäufigkeiten untergebracht, die mit der Nullhypothese am wenigsten vereinbar sind.

Bei der folgenden Tafeln sind die Summen aller Spalten und Reihen identisch mit der obigen:

	männl.	weibl.
genügend	4	0
ungenügend	1	3

	männl.	weibl.
genügend	1	3
ungenügend	4	0

Für den einseitigen Test wird

$\frac{{4 \choose 3}{4 \choose 2}}{{8 \choose 5}} + \frac{{4 \choose 4}{4 \choose 1}}{{8 \choose 5}}$

und für den zweiseitigen

$\frac{{4 \choose 3}{4 \choose 2}}{{8 \choose 5}} + \frac{{4 \choose 4}{4 \choose 1}}{{8 \choose 5}} + \frac{{4 \choose 1}{4 \choose 4}}{{8 \choose 5}}$

berechnet.

Siehe auch

• Vierfeldertest

Weblinks

• Fisher-Test online berechnen