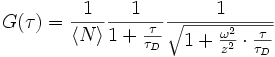Fluoreszenzkorrelationsspektroskopie

Die Fluoreszenz-Korrelations-Spektroskopie (fluorescence correlation spectroscopy, FCS) ist eine höchstempfindliche optische Messmethode, die aus Fluktuationen in der Fluoreszenzintensität Informationen gewinnt. Mit FCS werden in der Regel Diffusionskonstanten, Konzentrationen und Bindungen zwischen verschiedenen diffundierenden Spezies gemessen. Die Methode wurde in den 1970er Jahren von W. W. Webb, et al. entwickelt.

Aufbau

Schematischer Aufbau der FCS.

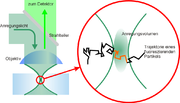
Die Grundlage für FCS bildet ein konfokales Mikroskop (siehe Abbildung). Das Anregungslicht wird mit Hilfe eines Objektives in die Probe fokussiert, sodass ein möglichst kleines Anregungsvolumen entsteht. Diffundieren nun fluoreszenzaktive Teilchen (z.B. fluoreszenzmarkierte Proteine) in das Anregungsvolumen, so werden diese dort zur Fluoreszenz angeregt. Dabei absorbieren die fluoreszenzaktiven Teilchen die Photonen des Anregungslichtes und emittieren ihrerseits Photonen größerer Wellenlänge, also geringerer Energie. Die emittierten Photonen größerer Wellenlänge können jetzt den (für das Anregungslicht undurchlässigen) Strahlteiler passieren und werden dann mit einem Fotodetektor detektiert. Wichtig für die FCS ist hierbei, dass die Detektoren mehrere Millionen mal in jeder Sekunde der Messung aufzeichnen, ob und falls ja wann genau ein Photon detektiert wurde.

(Auto-) Korrelationsfunktion

Fluoreszenz-Trace (oben) und daraus berechnete Korrelationsfunktion (unten, Kreise) sowie deren Anpassung mit nebenstehender Gleichung (unten, rote Linie).

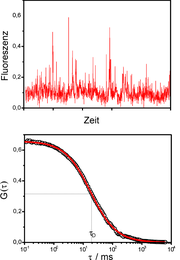
Die eigentliche Messgröße bei der FCS ist die Fluoreszenzintensität als Funktion der Zeit F(t), meist Trace (engl. für Spur) genannt. Die Abbildung (oben) zeigt einen Trace einer stark verdünnten Probe. Jede Spitze im Trace steht für ein fluoreszierendes Teilchen, das gerade durch das Anregungsvolumen diffundiert. Jedes dieser Teilchen braucht eine bestimmte Zeit, um den Fokus zu durchqueren. Deshalb ist die Wahrscheinlichkeit groß, dass zu aufeinanderfolgenden Abtastzeiten von ein und demselben Teilchen Photonen detektiert werden. Man spricht davon, dass die gemessenen Intensitäten zeitlich korreliert sind. Um die Traces auszuwerten, werden sie mit sich selbst korreliert (autokorreliert). Die Autokorrelationsfunktion G(τ) ist wie folgt definiert :

$G(\tau):=\frac{\langle \delta F(t) \delta F(t+\tau)\rangle}{\langle F(t)\rangle^2} = \frac{\langle F(t)F(t+\tau)\rangle}{\langle F(t)\rangle ^2}-1$.

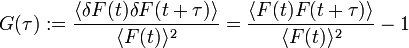Hierbei bedeuten die spitzen Klammern eine Mittelung über die Zeit, und $\delta F(t) = F(t) - \langle F(t) \rangle$.

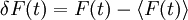Die Abbildung (unten) zeigt die Autokorrelation des Traces darüber, wobei man die logarithmische Skala der x-Achse beachten muss. Der Abfall der Autokorrelationsfunktion auf ihren halben Startwert ist ein Maß für die Diffusionszeit τ_D. Diese gibt an, wie lange ein Teilchen im Durchschnitt braucht, um das Anregungsvolumen zu durchqueren. Für die freie dreidimensionale Diffusion lässt sich zeigen, dass die Autokorrelationsfunktion wie folgt ausgedrückt werden kann:

$G(\tau)=\frac{1}{\langle N\rangle} \frac{1}{1+\frac{\tau}{\tau_D}} \frac{1}{\sqrt{1+\frac{\omega^2}{z^2}\cdot\frac{\tau}{\tau_D}}}$

Hierbei sind 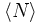$\langle N\rangle$ die mittlere Teilchenzahl im Anregungsvolumen (Fokus), ω der laterale Fokusdurchmesser und z der axiale Fokusdurchmesser. Die Intensitätsverteilung des Anregungslichtes wird hierbei als dreidimensionale Gauß-Funktion angenommen, was für viele Mikroskopobjektive eine gute Näherung darstellt.

Aus 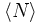$\langle N\rangle$ lässt sich die Konzentration C der fluoreszenzaktiven Teilchen in der Lösung angeben, wenn man das Anregungsvolumen V kennt: 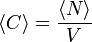$\langle C\rangle=\frac{\langle N\rangle}{V}$. Die Diffusionskonstante ergibt sich aus $D=\frac{\omega^2}{4\tau_D}$.

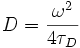Für zweidimensionale Diffusion (z.B. in Zellmembranen) entfällt der Wurzelterm.

Anwendungen

• In der Zellbiologie gibt es vermehrt Arbeiten, die FCS in lebenden Zellen durchführen. Mittlerweile gibt es eine Reihe von kommerziellen Herstellern von konfokalen Mikroskopen, die Korrelationsmessungen zulassen.

• Biotechnologie: Es werden Screening-Roboter angeboten, die auf Autokorrelationsmessungen basieren.

• In der Molekularen Biophysik kann man über die Abhängigkeit des Diffusionskoeffizienten vom hydrodynamischen Radius Rückschlüsse auf die Größe eines Proteins und damit, vor allem in Kombination mit FRET, seines Faltungszustands ziehen.

Literatur

• R. Rigler and E. Elson – Fluorescence Correlation Spectroscopy, Springer 2001
• M. Ehrenberg and R. Rigler – Rotational Brownian-motion and fluorescence intensity fluctuations. Chem. Phys. (1974) 4, 390–401.
• D. Magde, W. W. Webb, and E. Elson – Thermodynamic fluctuations in a reacting system—measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. (1972) 29, 705–708.
• D. Magde and E. Elson – Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers (1974) 13, 1-27.
• D. Magde, E. Elson and W. W. Webb – Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers (1974) 13, 29-61.

Weblinks

• www.biophysics.org/education (pdf-Format)