Fotogrammetrie

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Photogrammetrie (auch Fotogrammetrie oder Bildmessung) ist eine Gruppe von Messmethoden und Auswerteverfahren der Fernerkundung, um aus Fotografien und genauen Messbildern eines Objektes seine räumliche Lage oder dreidimensionale Form zu bestimmen. Im Regelfall werden die Bilder mit speziellen Messkameras aufgenommen.

Das Fachgebiet ist um 1900 aus der Geodäsie hervorgegangen und wird seit etwa zwei Jahrzehnten auch der Fernerkundung (FE, englisch Remote Sensing oder RS) zugeordnet. Wie die Mehrzahl der fernerkundlichen Verfahren ist auch die Photogrammetrie ein passives Fernerkundungs- und Vermessungsverfahren, da sie die berührungslose Rekonstruktion von räumlichen Objekten aus deren fotografisch festgehaltenen Strahlung ermöglicht. Die Objekte werden meist im natürlichen Licht und von mehreren Standpunkten der Kamera (oder gleichzeitig von mehreren Kameras) aufgenommen. Das vom Objekt in die Messkamera kommende Licht kann reflektierte oder emittierte Strahlung sein, künstliche Beleuchtung wird aber meist nur bei kleinen Objekten verwendet.

Überblick

Name und Schreibweise

Der Name taucht erstmals 1868 auf und kommt nicht - wie oft vermutet - vom Fotogramm, sondern soll als Abkürzung von Photographo-Metrie entstanden sein^[1]. Daher soll er auch nicht, wie die neue Rechtschreibung verlangen würde, mit drei m geschrieben werden.

Aufgaben der Photogrammetrie

Aufgaben und Methoden des Faches – das meist an Technischen Universitäten im Rahmen der Geodäsie gelehrt wird – sind nach Meyers Lexikon^[2] wie folgt:

Aufnahme und Auswertung ursprünglich nur fotografischer Messbilder zur Bestimmung von Beschaffenheit, Form und Lage beliebiger Objekte. Die Photogrammetrie erfährt heute eine bedeutende Ausweitung dank neuartiger Bildaufnahmegeräte und der digitalen Bildverarbeitung als Folge der Möglichkeiten von Optoelektronik, Computertechnik und digitalen Massenspeichern. Hauptanwendungsgebiet der Photogrammetrie ist die →Geodäsie.

Dazu kommen heute unter anderem die Herstellung von Landkarten, von digitalen GIS-Landschaftsmodellen und Spezialaufgaben wie etwa die Architektur- und Unfallphotogrammetrie sowie in medizinischen Anwendungen (z.B. Virtopsy).

Die terrestrische Photogrammetrie (Erdbildmessung), bei der die Messbilder von erdfesten Standpunkten aus aufgenommen werden (Fototheodolit), wird im geodätischen Bereich zum Beispiel bei topografischen Aufnahmen im Hochgebirge und bei Ingenieurvermessungen genutzt. Bei der Aerophotogrammetrie (Luftbildmessung) werden die Messbilder vorwiegend zur Herstellung topografischer Karten, für Katastermessungen und Aerotriangulationen mit einer →Messkammer vom Flugzeug aus aufgenommen (→Luftbild). Nach der Anzahl der verwendeten Bilder werden die Verfahren der Einbild-, Zweibildphotogrammetrie (Stereophotogrammetrie) und Mehrbildmessung unterschieden. Die Messbilder werden in Einzelbildauswertegeräten entzerrt oder an stereoskopischen Doppelbild-Auswertegeräten in drei Dimensionen ausgemessen.

Zu den nicht-geodätischen Anwendungen zählt die Vermessung von Architektur und Kunstwerken, die Ballistik (siehe auch Satellitenkamera), die Land- und Forstwirtschaft, die Röntgenologie, sowie Ingenieurbau und technisches Versuchswesen^[3].

Methodischer Überblick der Fachausdrücke

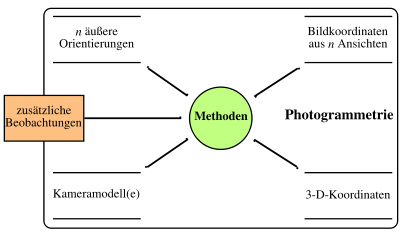Datenmodell der Photogrammetrie nach Wiora

Die nebenstehende Abbildung gibt einen Überblick über die Methoden der Photogrammetrie *) aus der Sicht der Eingangs- und Ausgangsgrößen.
(*) Im folgenden wird die von den offiziellen Vereinigungen des deutschen Sprachraums bevorzugte Schreibweise mit Ph benutzt.

Die 3D-Koordinaten sind die Ortskoordinaten von Objektpunkten im dreidimensionalen Raum. Die Bildkoordinaten geben den Ort der Abbildung der Objektpunkte auf die fotografische Platte, den Film oder einen elektronischen Bildwandler an. Die äußere Orientierung einer Kamera bezeichnet ihren Standort im Raum sowie ihre Blickrichtung. Die innere Orientierung definiert die abbildungsrelevanten Parameter der Kamera.
Der wichtigste dieser Parameter ist die Brennweite des Objektivs, es gehört aber auch die Beschreibung der Linsenverzerrungen dazu. Des Weiteren spielen die zusätzlichen Beobachtungen eine wichtige Rolle: Durch Maßstäbe, also den bekannten räumlichen Abstand zweier Punkte, oder Passpunkte, also die bekannten 3D-Koordinaten von Punkten in der Örtlichkeit (Objektpunkten), erfolgt die Anbindung an definierte Längeneinheiten und Koordinatensysteme.

Jede der vier Hauptgrößen kann als Voraussetzung oder als Ergebnis einer photogrammetrischen Methode betrachtet werden. Die einzelnen Methoden werden in den folgenden Abschnitten erläutert.

Grundlagen

Das Ziel einer photogrammetrischen Auswertung ist die Wiederherstellung der räumlichen Lage von Bildern zueinander, in der sie sich zum Zeitpunkt der Aufnahme befunden haben. Diese Wiederherstellung erfolgt nach den Gesetzen der Zentralprojektion unter Einhaltung der Komplanaritätsbedingung. Grundsätzlich kann man diese Berechnung in einem Guss im Zuge einer gemeinsamen Ausgleichung durchführen, verfahrenstechnisch zerfällt dieser Rechenvorgang jedoch in mehrere getrennte Schritte, die je nach der gegebenen Messungssituation untereinander kombiniert werden:

• Innere Orientierung: Um innerhalb eines Bildes messen zu können muss bekannt sein, wo sich der Bildhauptpunkt (entspricht idealerweise dem Bildmittelpunkt) befindet. Dieser Punkt wird durch den Strahl gebildet, der senkrecht auf der Objektivebene stehend durch den Brennpunkt in das Bild verläuft. Dieser Punkt, und hinzukommend auch noch die Kammerkonstante (i.A. die Brennweite) und die Objektivverzeichnung, wird messtechnisch ermittelt und erlaubt die Transformation eines gemessenen Punktes (x',y') in das Bildkoordinatensystem (x,y,c).
• Relative Orientierung: Wiederherstellung der relativen Lage zweier Bilder im Raum zueinander und Berechnung eines sogenannten Modells. Aus den Koordinaten der beiden Bilder P₁(x,y,c) und P₂(x,y,c) werden die Modellkoordinaten P₁₂(u,v,w) berechnet. In der Praxis lassen sich so zahlreiche Bilder, zum Beispiel aus Luftaufnahmen, zu einem Modellverbund zusammenrechnen.
• Äußere Orientierung: Im Gegensatz zur relativen Orientierung, bei der nur eine gegenseitige Wiederherstellung der Raumlage zweier Bilder erfolgt, erlaubt die äußere Orientierung die räumlich eindeutige Rekonstruktion der Bildlage bei der Aufnahme. Voraussetzung dazu ist allerdings, dass man über im Bild sichtbare Passpunkte in der Örtlichkeit verfügt, auf die man die Bildkoordinaten im Zuge eines räumlichen Rückwärtsschnittes iterativ einrechnet.
• Absolute Orientierung: Der Modellverbund aus der relativen Orientierung entspricht bereits der Geometrie der Punkte in der Örtlichkeit, allerdings stimmt die räumliche Orientierung des Modellverbundes noch nicht mit der Örtlichkeit überein und der Maßstab ist noch unbekannt. Im Zuge einer dreidimensionalen Helmert-Transformation werden die Modellkoordinaten des Modellverbundes auf die bekannten Passpunkte in der Örtlichkeit transformiert. Die Helmerttransformation passt die Punkte so in das bestehende Punktfeld ein, dass die Restklaffungen in den Koordinaten minimal werden. Bei Verwendung einer Restfehlerinterpolation lassen sich auch diese Klaffungen beseitigen.

Früher erfolgte die Auswertung zweier Luftbilder in Luftbildauswertegeräten, die die relative und absolute Orientierung durch physische Wiederherstellung der Strahlenbündel erreichte. Heute erfolgt die Auswertung in der Regel in Komparatoren, in denen Bildkoordinaten direkt gemessen werden. Die weiteren Arbeitsschritte sind dann Verfahrensgänge der numerischen Photogrammetrie, wobei Modellblock- und Bündelblockausgleichungsverfahren zum Einsatz kommen.

Zentralprojektion

Bei bekannter innerer und äußerer Orientierung und bekannten 3D-Koordinaten der Objektpunkte lassen sich daraus deren Bildkoordinaten berechnen. Das entspricht der fotografischen Abbildung der Objektpunkte bei bekannter Kameraposition. Der Berechnung liegt das Modell einer Lochkamera zugrunde die im Idealfall die technische Umsetzung der Zentralprojektion darstellt. Die mathematische Formulierung der Zentralprojektion sind die sogenannten Kollinearitätsgleichungen (s. a. Kollineare Abbildung), die gleichzeitig die zentralen Gleichungen der Photogrammetrie darstellen:

$x_c^{(i,j)} = s_x \cdot c \cdot \frac{r_{11}^{(i)} \cdot (x^{(j)}-x_0^{(i)}) + r_{12}^{(i)} \cdot (y^{(j)}-y_0^{(i)}) + r_{13}^{(i)} \cdot (z^{(j)}-z_0^{(i)})} {r_{31}^{(i)} \cdot (x^{(j)}-x_0^{(i)}) + r_{32}^{(i)} \cdot (y^{(j)}-y_0^{(i)}) + r_{33}^{(i)} \cdot (z^{(j)}-z_0^{(i)})}+ h_x + \Delta x \left( x_c^{(i,j)},y_c^{(i,j)} \right)$

$y_c^{(i,j)} = s_y \cdot c \cdot \frac{r_{21}^{(i)} \cdot (x^{(j)}-x_0^{(i)}) + r_{22}^{(i)} \cdot (y^{(j)}-y_0^{(i)}) + r_{23}^{(i)} \cdot (z^{(j)}-z_0^{(i)}) } {r_{31}^{(i)} \cdot (x^{(j)}-x_0^{(i)}) + r_{32}^{(i)} \cdot (y^{(j)}-y_0^{(i)}) + r_{33}^{(i)} \cdot (z^{(j)}-z_0^{(i)})}+ h_y + \Delta y \left( x_c^{(i,j)},y_c^{(i,j)} \right)$

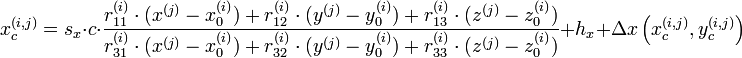
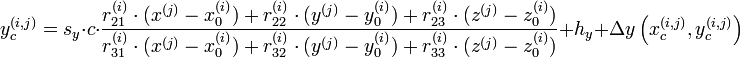
Die Bedeutungen der Symbole sind im Folgenden erklärt:

• i - Index zur Nummerierung der verschiedenen Kameras
• j - Index zur Nummerierung der verschiedenen Objekt- bzw. Bildpunkte
• c - Kammerkonstante, entspricht in etwa der Brennweite des Objektives
• r - 3×3 Rotationsmatrix zur Definition der Blickrichtung der Kamera
• (s_x,s_y)^T - Vektor zur Beschreibung der Asymmetrie der Bildpunkte von Matrixsensoren
• (x₀,y₀,z₀)^T - Vektor zur Definition des Projektionszentrums
• (x,y,z)^T - Vektor zur Definition der 3D-Koordinaten der Objektpunkte
• (h_x,h_y)^T - Vektor zur Definition der Lage des Bildhauptpunkts auf dem Film oder Sensor
• Δx und Δy - Funktionen zur Spezifizierung der Verzeichnungskorrekturen

Alternativ lässt sich die Bildkoordinate mit Hilfe der Projektive Geometrie (homogene Koordinaten) berechnen. Sie ist äquivalent zur klassischen Kollinearitätsgleichung.

x = PX

mit

P = KR[I | − Z]

• x - homogene Bildkoordinate (2d)
• X - homogener Raumpunkt (3d)
• P - Projektionsmatrix (3x4 Matrix)
• K - Kalibriermatrix mit Kamerakonstante, Hauptpunkt, Scherung und Maßstabsunterschied (3x3 Matrix)
• R - Rotationsmatrix
• I - Einheitsmatrix
• Z - Lage des Projektionszentrums (homogen)

Kamerakalibrierung

Bei der Kamerakalibrierung werden die Abbildungseigenschaften, also die innere Orientierung, der Kamera und die äußere Orientierung aus den bekannten Bild- und 3D-Koordinaten der Objektpunkte berechnet.

Bildmessung

Die Bildmessung bestimmt die exakten Bildkoordinaten der Abbildung eines Objektpunktes in einem Bild. Im einfachsten Fall erfolgt die Bildmessung manuell. Auf einem Negativ oder Positiv wird die Position des interessierenden Objektpunktes von einem Menschen mit einer Messvorrichtung bestimmt. Da diese Methode sehr fehleranfällig und langsam ist, verwendet man heute fast ausnahmslos computergestützte Verfahren zum Suchen und Vermessen von Objekten in Bildern. Dabei kommen Methoden der digitalen Bildverarbeitung und der Mustererkennung zum Einsatz. Man kann diese Aufgaben durch die Verwendung von künstlichen Signalmarken wesentlich vereinfachen. Diese können mit automatischen Methoden identifiziert und sehr präzise auf 1/50 bis 1/100 Pixel im Bild lokalisiert werden.

Rückwärtsschnitt

Der Rückwärtsschnitt berechnet die Kameraposition, also die äußere Orientierung aus der bekannten inneren Orientierung, den 3D-Koordinaten der Objektpunkte und ihren Bildkoordinaten. In der klassischen Geodäsie sind dafür mindestens drei Festpunkte erforderlich, während man bei Messbildern zur Genauigkeitssteigerung meist eine größere Zahl von Punkten heranzieht. (Anmerkung: im Normalfall sind 6 Passpunkte zur Orientierung eines Messbildes erforderlich).

Vorwärtsschnitt

Mit einem Vorwärtsschnitt kann man bei mindestens zwei bekannten äußeren Orientierungen und den dazugehörigen Bildkoordinaten die 3D-Koordinaten der Objektpunkte berechnen. Voraussetzung ist, dass mindestens zwei Fotografien eines Objektes aus unterschiedlichen Richtungen aufgenommen wurden, ob gleichzeitig mit mehreren Kameras oder sequentiell mit einer Kamera spielt dabei für das Prinzip keine Rolle.

Modellblockausgleichung

Zwei Bilder in einem analogen oder analytischen Auswertegerät sind relativ zu orientieren. Die entstehenden räumlichen Modellkoordinaten werden mit Hilfe verketteter dreidimensionaler Helmert-Transformationen in einer gemeinsamen Ausgleichung auf die Erdoberfläche transformiert (absolute Orientierung). Die Numerik der zu lösenden Gleichungen besteht lediglich aus Rotationen, Translationen und einem Maßstab. Durch Bezug der Koordinaten auf ihren Schwerpunkt zerfallen die Normalgleichungen des Ausgleichungssystems und die zur Ausgleichung eines Modells notwendigen 7 Unbekannten reduzieren sich auf zwei Normalgleichungen mit 4 und 3 Unbekannten. Da die Numerik nicht allzu anspruchsvoll ist, fand dieses Berechnungsverfahren weite Verbreitung. Ein Ende der 70er Jahre an der Universität Stuttgart entwickeltes Programmsystem führte die Bezeichnung PAT-M43 (Programmsystem Aerotriangulation - Modellblockausgleichung mit 4 bzw. 3 Unbekannten). Die erreichbaren Genauigkeiten bei Modellblockausgleichungen ergeben mittlere Fehler für die Lage von ± 7 µm und für die Höhe von ± 10 µm.
Ähnliche Programmsysteme entstanden mit dem Orient (Photogrammetrie) der TU Wien und auf anderen Hochschulen.

Bündelblockausgleichung

Die Bündelblockausgleichung ist das wichtigste Verfahren der Photogrammetrie. Mit ihr kann man aus groben Näherungswerten für äußere und innere Orientierung gleichzeitig alle unbekannten Größen der Kolinearitätsgleichungen berechnen. Als bekannte Größe benötigt man lediglich die Bildkoordinaten der Objektpunkte, sowie zusätzliche Beobachtungen in Form eines Längenmaßstabes oder die räumlichen Koordinaten von Passpunkten. Diese Methode ist das am häufigsten eingesetzte Verfahren der Photogrammetrie bei statischen Messobjekten. Der Hauptvorteil liegt vor allem in der Möglichkeit einer Simultankalibrierung. Das heißt, dass die Messkamera während der eigentlichen Messung kalibriert wird. Mess- und Kalibrieraufnahmen sind also identisch, was den Aufwand für die Messung reduziert und gleichzeitig garantiert, dass die Messkamera stets kalibriert ist. Allerdings eignen sich nicht alle Konfigurationen von Objektpunkten für eine Simultankalibrierung. Dann müssen entweder zusätzliche Objektpunkte in die Messung miteinbezogen werden oder separate Kalibrieraufnahmen gemacht werden.

Die Bündelblockausgleichung basiert, wie der Name sagt, auf der gemeinsamen Berechnung von Bündelblöcken. Von der theoretischen Seite her ist es im Vergleich mit der Modellblockausgleichung das strengere Verfahren. Die Beschaffung der Ausgangsdaten ist allerdings einfacher. Die weitere Berechnung über die Modellbildung bis zur absoluten Orientierung erfolgt in einer einzigen Ausgleichungsrechnung. Die Anforderungen an die Numerik sind allerdings wesentlich höher als bei der Modellblockausgleichung: die Normalgleichungen zerfallen nicht und die Anzahl der Unbekannten ist mit bis zu mehreren Tausend deutlich höher.

Einteilung

Nach der verwendeten Methode der Bildmessung und der anschließenden Auswertung teilt man die Photogrammetrie auch in analoge Photogrammetrie mit optisch-mechanischer Fotografie und Auswertung, analytische Photogrammetrie mit optisch-mechanischer Fotografie und rechnergestützter Auswertung, digitale Photogrammetrie mit digitaler Fotografie und rechnergestützter Offline-Auswertung, sowie digitale Onlinephotogrammetrie mit digitaler Fotografie und Online-Bildmessung ein.

Anwendungen

Die Photogrammetrie lässt sich in die zwei Hauptanwendungsgebiete Luftbildphotogrammetrie und terrestrische bzw. Nahbereichsphotogrammetrie einteilen.

Luftbildphotogrammetrie

Bei der Luftbildphotogrammetrie werden die Fotografien mit flugzeuggetragenen, digitalen oder analogen Messbildkameras aufgenommen. Es entstehen meist regelmäßige, streifenweise angeordnete Bildverbände, in denen sich benachbarte Bilder deutlich überlappen. Die Bildverbände werden orientiert, also in ein gemeinsames Koordinatensystem transformiert. Die Orientierung der Bildverbände erfolgt anhand von Pass- und Verknüpfungspunkten im Rahmen einer Bündelblockausgleichung. Aus den orientierten Bildern können Folgeprodukte wie 3D-Punkte, digitale Geländemodelle (DGM), Orthophotos, etc., abgeleitet werden.

Die Ergebnisse der Luftbildphotogrammetrie dienen der Erstellung und Fortführung topographischer Karten und Orthophotos, der großmaßstäbigen Punktbestimmung in Liegenschaftskatastern und zur Flurbereinigung. Es können auch digitale Geländemodelle (DGM) aus den Daten abgeleitet werden. Die Landnutzungserhebung sowie Umwelt- und Leitungskataster profitieren ebenfalls von den Resultaten der Luftbildphotogrammetrie.

Nahbereichsphotogrammetrie

Die Nahbereichsphotogrammetrie befasst sich mit Objekten in einem Größenbereich von wenigen Zentimetern bis zu rund 100 Metern. In der Nahbereichsphotogrammetrie gibt es, anders als in der Luftbildphotogrammetrie, keine Einschränkungen bei der Aufnahmeanordnung. Es können beliebige Aufnahmepositionen verwendet werden wie sie entstehen, wenn man ein Objekt mit einer Handkamera von mehreren Richtungen fotografiert. In der Regel benutzt man dazu heute hochauflösende Digitalkameras.

Die häufigsten Anwendungsfelder der Nahbereichsphotogrammetrie sind die industrielle Messtechnik (s. Streifenprojektion), Medizin und Biomechanik, sowie die Unfallaufnahme. In der Architektur und Archäologie nutzt man die Nahbereichsphotogrammetrie zur Bauaufnahme, also zur Dokumentation als Grundlage von Umbauten und denkmalpflegerischen Maßnahmen.

Ein wichtiges Nebenprodukt der Nahbereichsphotogrammetrie sind entzerrte Fotografien. Das sind Fotografien von nahezu ebenen Objekten wie Gebäudefassaden die so auf eine Fläche projiziert werden, dass die Abstände im Bild über einen einfachen Maßstab in metrische Längen und Abstände umgerechnet werden können.

In jüngster Zeit hat auch die moderne Kinematographie Techniken aus der Photogrammetrie übernommen. Im Film Fight Club wurden mit dieser Technik zum Beispiel interessante Kamerafahrten ermöglicht.

Geschichte

Die Theorie der Photogrammetrie wurde Mitte des 19. Jahrhunderts in Frankreich und Preußen parallel zur aufkommenden Photographie entwickelt. Der französische Offizier Aimé Laussedat (*19. April 1819 in Moulins (Allier), †1904) veröffentlichte 1851 seine Schrift Métrophotographie, der deutsche Architekt Albrecht Meydenbauer (*1832, †1921) publizierte 1858 sein photogrammetrisches Verfahren zur Gebäudevermessung. Er gab der Photogrammetrie ihren Namen und gründete 1885 die erste photogrammetrisch arbeitende Behörde der Welt, die Königlich Preußische Messbild-Anstalt. Auch Édouard Gaston Deville und Paul Gast waren einige der Pioniere dieser Methode. In den 1930er Jahren wurde durch Gast die Bündelblockausgleichung (basierend auf der von Carl Friedrich Gauß erdachten Ausgleichsrechnung), wie er sie 1930 in seinem Werk "Vorlesung über Photogrammetrie" publizierte, entwickelt, die seit den 1960er Jahren in großem Stil auf Computern eingesetzt wird. Als ab Ende 1980er großformatige Photoscanner für Luftbilder bzw. Videokameras und Digitalkameras für Nahbereichs-Aufnahmen verfügbar waren, wurden die analogen Methoden der Photogrammetrie in den meisten Anwendungen durch digitale Auswerteverfahren ersetzt. Derzeit (2005) vollzieht sich der letzte Schritt zur Volldigitalisierung, indem auch in der Luftbildphotogrammetrie die herkömmlichen film-basierten Kameras zunehmend von digitalen Sensoren abgelöst werden.

Siehe auch

• Radargrammetrie
• Deutsche Gesellschaft für Photogrammetrie, Fernerkundung und Geoinformation (DGPF) e.V.
• Stereoskopie
• Albrecht Meydenbauer

Literatur

• Karl Kraus: Photogrammetrie. de Gruyter, Berlin 2004, ISBN 3-11-017708-0
• Thomas Luhmann: Nahbereichsphotogrammetrie. Wichmann, Heidelberg 2003, ISBN 3-87907-398-8
• McGlone, Mikhail, Bethel (Hrsg.): Manual of Photogrammetry. ASPRS, Bethesda MD ⁵2004, ISBN 1-57083-071-1
• Alparslan Akça, Jürgen Huss (Hrsg.) et al.: Luftbildmessung und Fernerkundung in der Forstwirtschaft. Wichmann, Karlsruhe 1984, ISBN 3-87907-131-4

Nachweise

1. ↑ Gemeinsame Erklärung der DGPF, ÖVG und SGPBF, 1999
2. ↑ http://lexikon.meyers.de/index.php/Fotogrammetrie
3. ↑ K.Kraus 2004, F.K. List 1998

Weblinks

• Photogrammetrie bei der Verkehrsunfallaufnahme (Phidias)

Fachverbände

• DGPF - Deutsche Gesellschaft für Photogrammetrie, Fernerkundung und Geoinformation
• ISPRS - International Society for Photogrammetry and Remote Sensing
• CIPA - International Scientific Committee of ICOMOS for Heritage Documentation
• SGPBF - Schweizerische Gesellschaft für Photogrammetrie, Bildanalyse und Fernerkundung