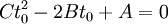GPS-Grundgleichungen

Die Artikel GPS-Technologie und Global Positioning System überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. FordPrefect42 22:40, 3. Nov. 2008 (CET)

GPS-Technologie

Beim Global Positioning System (GPS) wird der Ort des Empfängers - genauer der Ort der Empfangsantenne - mit Hilfe der Entfernung zu mehreren Satelliten bestimmt. Ein Satellit reicht nicht, denn bei einer gegebenen Entfernung zu einem Satelliten kann sich der Empfänger irgendwo auf einer Kugeloberfläche mit dem Radius der Entfernung befinden, in deren Mittelpunkt der Satellit ist. Wenn weitere Informationen bekannt sind, engt sich die Unbestimmtheit des Ortes ein. Wenn bekannt ist, dass der Empfänger auf der Oberfläche der Erdkugel ist, so kann sich der Empfänger nur auf dem Kreis befinden, der die Schnittlinie Erdkugel-Entfernungskugel ist. Ist bekannt, dass sich Sendeort und Empfänger auf einer Ebene befinden, ist ein Kreis die Schnittlinie der Kugeloberfläche mit der Ebene.

Bei zwei Entfernungen und zwei Kugelmittelpunkten ist der mögliche Ort des Empfängers schon eingeschränkt, da der Empfänger sich nur an Orten befinden kann, die sich gleichzeitig auf beiden Kugelflächen befinden. Diese Orte sind die Schnittlinie der beiden Kugeloberflächen. Die Schnittlinie zweier Kugeloberflächen ist ein Kreis im Raum. Kommt eine weitere Entfernung mit einem weiteren Kugelmittelpunkt hinzu, so ist der Empfängerort der Ort, wo sich alle drei Kugeloberflächen schneiden, denn nur an diesem Ort (ggf. auch zwei Orte) hat der Empfänger zu allen gegebenen Kugelmittelpunkten, die mit den Satellitenorten übereinstimmen, die gegebenen Entfernungen. Rechnerisch drückt sich das in einem kartesischen Koordinatensystem wie folgt aus:

Im Koordinatensystem kann jeder Ort durch die Angabe von drei Koordinaten eindeutig bestimmt werden. Da für den gesuchten Ort dementsprechend drei Ortskoordinaten bestimmt werden müssen, sind drei Gleichungen erforderlich, um die drei unbekannten Ortskoordinaten zu bestimmen. Die erforderlichen drei Gleichungen ergeben sich aus den Entfernungen zu den drei Kugelmittelpunkten (Satelliten). Die Lösung der Gleichungen ist in realen Fällen immer möglich. Würden beliebige Orte und Entfernungen vorgegeben, so ergibt sich keine Lösung, wenn sich die Kugeloberflächen nicht schneiden - was bei realen Aufgaben aber immer der Fall ist.

Die Realisierung dieses Prinzips hat beim GPS zwei prinzipielle Schwierigkeiten:

• die Entfernung kann nicht direkt gemessen werden.
• die Satelliten bewegen sich (mit ca. 3,9 km/s), wodurch sich der Ort der Kugelmittelpunkte im Laufe der Zeit schnell verändert.

Zur Behebung der ersten Schwierigkeit benutzt man die Laufzeit des Signals, d.h. um wie viel später das Signal beim Empfänger ankommt - und rechnet in erster Näherung damit, dass sich das Signal mit der Vakuumlichtgeschwindigkeit bewegt. Als Beispiel für die Art der Entfernungsbestimmung ist die Entfernungsbestimmung beim Gewitter bekannt: Wenn man einen Blitz sieht (die Laufzeit des Blitzes ist zu vernachlässigen), wird bestimmt, wie lange es dauert, bis der Donner zu hören ist. Aus dieser Laufzeit des Donners wird mit Hilfe der Schallgeschwindigkeit die Entfernung bestimmt. Zu welcher Uhrzeit Blitz und Donner dem Empfänger bekannt werden, ist dabei unerheblich.

Diese einfache Laufzeitbestimmung analog der Differenz zwischen Blitz und Donner ist beim GPS etwas komplizierter, da dem Empfänger zunächst fehlt, wann das empfangene Signal ausgesandt wurde. Da Sender und Empfänger der auszuwertenden Informationen beim GPS-System nicht miteinander in Wechselwirkung treten oder kommunizieren können, handelt es sich um eine unidirektionale Entfernungsmessung.

Beim GPS ist diese Entfernungsmessung so gelöst, dass das empfangene Signal seinen Sendezeitpunkt mitbringt - und zwar in Form der GPS-Systemzeit bei der Sendung. Wenn der Empfänger die GPS-Systemzeit kennt, kann er die Laufzeit als die Differenz zwischen Sendeuhrzeit und Empfangsuhrzeit bestimmen. In der Regel kennt der Empfänger aber nicht seine Empfangszeit in der GPS-Systemzeit. Deshalb ist der Empfangszeitpunkt in der GPS-Systemzeit eine weitere Unbekannte zur Ortsbestimmung. Da deshalb vier Unbekannte zu bestimmen sind, werden auch vier Gleichungen zur Bestimmung der vier Unbekannten (drei Ortskoordinaten und der Empfangszeitpunkt in der GPS-Systemzeit) benötigt. Diese vierte Gleichung erfordert die Hinzunahme der Entfernung zu einem vierten Satelliten.

Zur Erklärung, warum das möglich ist: Wird eine falsche Empfangszeit benutzt, so sind die Entfernungen zu den Satelliten auch falsch. Nimmt man von den vier falschen Entfernungen nur drei, lässt sich damit ein möglicher (falscher!) Ort des Empfängers bestimmen. Sogar die Wahl des Empfangszeitpunktes ist aber schon eingeschränkt - denn nur für bestimmte Entfernungsbereiche kann das System der drei Gleichungen gelöst werden: sind die Entfernungen zu falsch, schneiden sich nicht alle drei Kugeln. Außerdem sind die falschen Empfängerorte unterschiedlich - je nachdem, welche der drei Entfernungen aus den vier (falschen) Entfernungen gewählt wurden. Nur beim richtigen Empfangszeitpunkt sind alle Empfängerorte gleich und damit richtig. Deshalb muss das System der vier Gleichungen gelöst werden.

Die Kenntnis des Sendezeitpunktes ist auch noch aus einem weiteren Grund wichtig: Weil sich die Satelliten bewegen, muss der Sendeort zum Sendezeitpunkt bekannt sein. Der Satellit kann in dem kurzem Sendeaugenblick seine Koordinaten nicht übertragen. Deshalb wird zur Ortsbestimmung die Bahngleichung als Zeitfunktion benutzt. Die Konstanten, die die Bahngleichung enthält, werden mit dem Signal übertragen.

Anmerkung: Je nach Anzahl der schon bekannten Größen reduziert sich die Zahl der Unbekannten und damit die Mindestanzahl der zu empfangenden Satelliten. Ist die Zeit (genau!!) bekannt, so sind nur noch 3 Unbekannte und es sind nur 3 Satelliten notwendig, ist zusätzlich die Höhe bekannt (z. B. Höhe = 0 auf der Erdoberfläche), so sind nur noch 2 Unbekannte und es sind nur 2 Satelliten notwendig, ist darüber hinaus noch der Breitengrad bekannt, so ist nur noch 1 Unbekannte vorhanden und es ist nur 1 Satellit notwendig.

Zur Ortsbestimmung wurde im vorherstehenden Text die Vakuumlichtgeschwindigkeit benutzt. Zur genauen Ortsbestimmung muss berücksichtigt werden, dass auf dem Weg zwischen Satelliten und Empfänger kein Vakuum herrscht. Im Nichtvakuum ist die Signalgeschwindigkeit geringer. Die Entfernung Satellit - Empfänger wird deshalb bei Benutzung der Vakuumlichtgeschwindigkeit zu groß berechnet. Wird trotzdem die Vakuumlichtgeschwindigkeit benutzt, muss die tatsächliche Laufzeit um die zusätzliche Ausbreitungszeit korrigiert werden. Da die Verzögerung hauptsächlich in der Ionosphäre erfolgt, nennt man das Ionosphärenkorrektur. Zur Technik der Ortsbestimmung gehört auch die Berücksichtigung von vermeidbaren und unvermeidbaren Signalstörungen. Damit ergeben sich folgende einzelne Abschnitte zur Beschreibung der GPS-Technologie:

Beschreibung des GPS-Signals

Grundlegend unterschieden wird das GPS Signal in zwei getrennte Signale. Das zivile L1-Signal mit einer Trägerwelle von 1575,42 MHz und dem verschlüsselbaren L2-Signal mit einer Trägerwelle von 1227,60 MHz. Im L1-Signal wird der im folgenden näher erläuterte C/A-Code übertragen und im L2-Signal der verschlüsselte und nicht öffentlich bekannte P-Code. Jedes dieser beiden Signale besteht aus je drei Anteilen: Trägerwelle, Code und Navigationsdaten.

Wie vorstehend beschrieben, muss jeder Satellit seine Bahndaten (Ephemeriden) und seinen Sendezeitpunkt seinem Sendesignal mitgeben. Diese Mitteilung erfolgt mit den C/A-Daten. Außerdem muss es dem Empfänger möglich sein, zu bestimmen, von welchem Satelliten das empfangene Signal stammt – obwohl alle Satelliten die gleiche Sendefrequenz benutzen. Zur Erfüllung all dieser Anforderungen wurde das GPS-Signal entwickelt, welches ein CDMA-Modulationsverfahren ist. Zeitrelevant sind immer die Zeitpunkte des Beginns eines Signalteiles, wobei verschiedene Signalteile unterschiedliche Dauer haben – aber alle Signalteile sind gleichzeitig vorhanden.

Bezugszeit aller Signale ist Sonntag 0 Uhr. In den übertragenen Nachrichten ist auch die Nummer der Woche enthalten. Diese Information ist allerdings für die Ortsbestimmung nicht relevant. Die nächste Signaleinheit ist der Subframe. Ein Subframe hat eine zeitliche Länge von 6 s und trägt zu Beginn eine Nachricht, wie oft 6 s seit Sonntag 0 Uhr am Sendebeginn des nächsten Subframe vergangen sind. Die nächst kleinere Einheit ist das Word. Ein Subframe besteht aus 10 Worten. Diese kleinere Einheit Word besteht aus 30 Nachrichtenbits. 24 Bits tragen die Nachrichten direkt, am Schluss jedes Words sind sechs Paritybits vorhanden, um den fehlerfreien Empfang zu kontrollieren. Die einzelnen Wörter tragen keine Information über ihre Sendezeit, die Sendezeit des Wordanfangs ergibt sich durch Abzählen ihrer Stellung im Subframe. Ohne Abzählen wäre die Sendezeit des Wordanfangs um 0,6 s mehrdeutig.

Jedes Nachrichtenbit dauert 0,02 s (= 20 ms) und enthält natürlich auch keine weitere Information. Die genaue Zeitlage seines Beginns ergibt sich durch Abzählen innerhalb des Wortes. Ohne Abzählen wäre die Sendezeit des Beginns jedes Nachrichtenbits um 20 ms mehrdeutig. Jedes Nachrichtenbit ist unterteilt in 20 Codeblöcke. Diese 20 Codeblöcke mit einer Dauer von 1 ms sind identisch und bestehen aus einer Folge von je 1023 Chips. Zur Unterscheidung von den Nachrichtenbits werden die Bits der CDMA-Codeblöcke als Chips bezeichnet. Da jeder Codeblock 1 ms dauert und auch keine Nachricht tragen kann, muss seine Zeit wieder durch Abzählen bestimmt werden, innerhalb seines Bits, bzw. Words bzw. Subframes. Ohne Abzählen wäre die Sendezeit des Beginns jedes Codeblocks um 1 ms mehrdeutig.

Eine Folge von 1023 Chips kann auf 2¹⁰²³ (ca. 8,99 · 10³⁰⁷) Arten gebildet werden. Damit trotz der vielen Möglichkeiten die gewählte Folge für jeden Satelliten einzigartig ist, wird eine Folge aus den Gold-Codes [1] benutzt. Gold-Codes haben eine Länge von 2ⁿ − 1 Bit. n ist dabei eine Ganzzahl, die bei GPS zu 10 gewählt wurde. Im Empfänger wird für jeden empfangenen Satelliten eine identische Gold-Code-Folge erzeugt. Zunächst haben die empfangene und die im Empfänger selbst erzeugte Code-Folge keine zeitliche Beziehung. Um diese zeitliche Beziehung herzustellen, werden beide Folgen miteinander multipliziert und die Multiplikationsergebnisse addiert. Diese Prozedur wird als Kreuzkorrelation bezeichnet. Wenn der zeitliche Unterschied variiert wird, ändert sich die Summe. Die Summe wird maximal, wenn die Folgen zeitlich übereinstimmen. Die Code-Folgen wurden beim GPS so gewählt, dass gesichert ist, dass nur bei der richtigen Code-Folge und bei der richtigen Zeitverschiebung das Maximum auftritt (Einzigartigkeit). Die im Empfänger erzeugte Code-Folge kann mit einem Zeitfehler < 1 ns an die empfangene Code-Folge, die vom Satelliten gesendet wurde, angepasst werden. Durch das Abzählen in den Signaleinheiten und die Lage der momentanen Zeit im Codeblock ist der genaue Sendezeitpunkt bekannt.

Zusätzlich zu diesem auf einer Gold-Folge basierenden C/A-Code wird mit 50 bit/s die Navigationsnachricht in das L1-Signal mit hineinmoduliert. Sie besteht aus einem 50-Hz-Signal und enthält Daten wie die Satellitenbahnen, Uhrenkorrekturen und andere Systemparameter (z. B. den Status der Satelliten, also ob in Ordnung oder fehlerhaft). Diese Daten werden ständig von jedem Satelliten übermittelt. Daraus erhält der GPS-Empfänger sein Datum, die ungefähre Uhrzeit und die Positionen der Satelliten.

Modulation des GPS-Signals auf den Träger

Das Signal hat die zwei Werte 0 und 1. So kann das Signal nicht direkt übertragen werden. Zur Übertragung wird eine Trägerfrequenz gesendet, deren Phase je nach Signalwert um 180° geändert wird. Bei einer 0 wird die Trägerfrequenz direkt, bei einer 1 die um 180° phasenverschobene Trägerfrequenz gesendet.

Bestimmung der Sendezeitpunkte

Wie schon erwähnt, erzeugt der Empfänger für jeden Satelliten eine eigene Codefolge und verschiebt diese Codefolgen so, dass jede Codefolge maximal mit dem dazugehörigen Satelliten übereinstimmt. Damit ist der Sendezeitpunkt jedes Satellitensignals bekannt.

Bild: Die Verhältnisse am Empfänger beim Empfang der GPS-Satelliten.

Im Bild sind von den gleichzeitig empfangenen Satellitensignalen nur die Signale von zwei Satelliten dargestellt (rot und grün). Ein Bit der GPS-Nachricht ist 20 Codeblöcke lang (von denen jeder 1023 Chips (CDMA-Codebits) lang ist). Dargestellt ist das nur mit fünf Codeblöcken. Zu welcher Zeit der Empfänger die Auswertung vornimmt (magenta), ist nicht von Bedeutung. Welche Zeit an der blauen Zeitrichtung steht (Empfängerzeit), ist auch gleich. Für die Auswertung muss nur die Zeit des Beginns eines Codeblocks im Satelliten bekannt sein, und der Empfänger muss nur die Zeit zwischen Auswertezeitpunkt und Beginn eines Codeblocks messen. Die Sendezeit des Codeblocks wird durch Auswertung der Satellitennachricht bestimmt.

Die Bestimmung der Lage eines Codeblocks war schon beschrieben. Nach der Bestimmung der Lage des Empfangszeitpunkts innerhalb eines Codeblocks muss nun die Lage des Codeblocks zu Sonntag 0 Uhr bestimmt werden. Dazu muss der Empfänger von der Einheit Codeblock rückwärts immer die größere Einheit bestimmen, um die Lage des Codeblocks zu Sonntag 0 Uhr bestimmen zu können:

• Zuerst wird bestimmt, bei welchen aufeinanderfolgenden Codeblöcken die Reihenfolge zwischen Einsen (mit dazwischen liegenden Nullen) und Nullen (mit dazwischen liegenden Einsen) wechselt. Dieser Wechsel ist der Anfang eines Nachrichtenbits. Damit ist der Abstand zu Sonntag 0 Uhr mit einer Unsicherheit von Vielfachen von 20 ms bestimmt.

Anmerkung: Ein Wechsel muss nicht nach spätestens 20 ms erfolgen, da es mehrere aufeinanderfolgende Nullen oder Einsen geben kann, sodass nicht alle 20 ms ein solcher Wechsel erfolgt. Aber in einer Dauer von 0,6 s (Dauer der Wordlänge) sind wegen der Paritätsbits mit Sicherheit mehrere Bitwechsel.

Nachdem die Bitgrenze erkannt ist, können die Bits empfangen und gespeichert werden. In dieser Bitfolge ist nun die Lage der Subframes zu bestimmen, von der jeder 300 bit lang ist.

• Danach wird die Lage eines Subframe identifiziert. Dazu braucht der Empfänger die doppelte Subframelänge, also mindestens 600 empfangene Bits, die er in 12 s empfängt.

Aus der gespeicherten Bitfolge nimmt der Empfänger einen Block von 600 Bits und sucht in diesem Block nach der Bitfolge 10001011. Diese Bitfolge ist im ersten Word jedes Subframe enthalten. Dieses erste Word wird als TLM-Word (=Telemetry-Word) bezeichnet. Die gesuchte Bitfolge, die im TLM-Word enthalten ist, wird als Preamble bezeichnet. Mit der Identifizierung dieser Bitfolge ist der Beginn jedes Subframe und jedes Wortes bekannt, da alle Wörter jeweils 30 bit lang sind. Da allerdings die Bitfolge 10001011 auch in der übrigen Nachricht auftreten kann, müssen zur Überprüfung, ob es wirklich der Beginn des TLM-Words ist, noch zwei Prüfungen erfolgen. Erstens: wenn es sich bei der gefundenen Bitfolge tatsächlich um die Preamble handelt, sind die 6 Paritybits am Ende jedes Words richtig, und zweitens muss alle 300 Bit (6 s) ein neuer Subframe kommen, der immer mit einem TLM-Word beginnt. Wenn die Prüfung erfolgreich ist, ist damit der Beginn jedes Subframes in der Empfängerzeit bekannt. Die Sendezeit jedes Framebeginns im Satelliten ist noch unsicher in Vielfachen von 6 s.

Anmerkung: Wenn der Empfänger eine ggf. falsche Identifizierung feststellt, wird in dem 600-Bit-Block nach einer weiteren 10001011-Folge gesucht und überprüft, ob es sich nun um die Preamble handelt.

Zur Identifizierung wie oft 6 s seit Sonntag 0 Uhr vergangen sind, wird das dem TLM-Word folgende HOW (Hand over Word) ausgewertet. Die ersten 17 Bits des HOW geben die Zeit des Beginns des nachfolgenden Subframes als ganzzahlige Zählzahl von 6 sec seit Sonntag 0 Uhr an. Damit ist in der Empfängerzeit immer bekannt, wann jede Aussendung in der GPS-Zeit erfolgt, da die eben beschriebene Prozedur bei jedem empfangenen Signal eines Satelliten erfolgt.

Damit ist in der empfängereigenen Zeit bekannt, zu welchem Zeitpunkt das gerade (eben zur Empfängerzeit) empfangene Signal ausgesandt wurde.

Bestimmung der Satellitenorte zum Sendezeitpunkt

In der Satellitennachricht sind die Bahnparameter jedes Satelliten enthalten. Mit den Bahnparametern und der Sendezeit kann für jede Sendezeit der Satellitenort berechnet werden.

Ablauf der Zeitbestimmung

Zuerst verschiebt der Empfänger in der empfängereigenen Zeit (Empfängerzeit) den im Empfänger selbst erzeugten Codeblock (= 1 Chip) so lange (im Bereich von 1 ms), bis das Korrelationsmaximum auftritt. Die Verschiebung erfolgt mit einer DLL (Delay-Locked Loop – Verzögerungsregelschleife). Damit ist zeitlich der Beginn jedes Codeblocks in der Empfängerzeit bekannt =Ankunftszeit). Und die Sendezeit ist unsicher in Vielfachen von 1 ms.

Nun sucht der Empfänger nach Bitwechseln in der Navigationsnachricht. Die Dauer eines Bits beträgt 20 ms = 20 Chips. Damit ist die Übertragungsrate 50 Bits pro Sekunde und bestimmen eine 20 ms-Zeit-Raster. Wenn 0-Bits oder 1-Bits aufeinanderfolgen kann kein Wechsel festgestellt werden. Da aber die Navigationsnachricht mit Sicherheit nicht nur aus fortlaufenden 0 oder fortlaufenden 1 besteht, taucht irgendwann ein Bitwechsel auf. Der Zeitpunkt des Auftretens dieses Bitwechsels ist damit in der Empfängerzeit bekannt. Wegen des 20 ms-Zeit-Rasters ist damit außerdem auch die Sendezeit jedes Bitwechsels nur noch unsicher in Vielfachen von 20 ms.

Der Empfänger speichert nun die empfangene Bitfolge. In der Empfängerzeit ist der Beginn jedes Bits genau bekannt (auf weniger als 1 ns).

In dem erhalten Bitstrom nimmt der Empfänger einen Block von mindestens 330 Bits (=10 + 1 Wörter = 6,6 sec) und sucht in dem Block nach der Bitfolge 10001011 (genauer auch noch nach 01110100, weil anfangs noch nicht bekannt ist, was 0 und was 1 ist). Diese Bitfolge ist die Preamble im TLM-Word (=Telemetry-Word). Mit der Identifizierung dieser Bitfolge ist der Beginn jedes TLM-Wortes bekannt, da alle TLM-Wörter jeweils 30 bit lang sind. Da allerdings die Bitfolge 10001011 auch in der übrigen Nachricht auftreten kann, müssen zur Überprüfung ob es wirklich der Beginn des TLM-Words ist, noch zwei weitere Prüfungen erfolgen: Erstens wenn es sich bei der gefundenen Bitfolge tatsächlich um die Preamble handelt, sind die 6 Paritybits am Ende jedes TLM-Words richtig und zweitens muß alle 300 Bits (6 s) ein neuer Subframe kommen, der immer mit dem TLM-Word beginnt. Wenn die Prüfung erfolgreich ist, ist damit der Beginn jedes Subframes in der Empfängerzeit bekannt. Die Sendezeit jedes Subframebeginns ist so nur noch unsicher in Vielfachen von 6 sec.

Anmerkung: Wenn der Empfänger eine ggf. falsche Identifizierung feststellt, wird in dem 330-Bit-Block nach einer weiteren 10001011-Folge gesucht und überprüft, ob es sich nun um die Preamble handelt.

Nun wird das dem TLM-Word folgende HOW-Word (Hand over Word) ausgewertet. Die ersten 17 Bits geben die Zeit des Beginns des nachfolgenden Subframes als ganzzahlige Zählzahl von 6 sec seit Sonntag 0 Uhr an.

Die empfangenen Bits wurden synchron zum Zeitrahmen der Satellitenzeit (interne Zeit von jedem einzelnen Satelliten) ausgesendet. Da die Satellitenzeit nicht exakt identisch mit der GPS-Systemzeit ist, werden in der Navigationsnachricht Korrekturwerte zur Zeitbestimmung im Subframe 1 mit übertragen. Anhand der zeitkorrekturwerte kann die genaue GPS-Zeit der Aussendung berechnet werden.

Damit ist in der Empfängerzeit immer bekannt, wann jede Aussendung in der GPS-Zeit erfolgt, da die eben beschriebene Prozedur bei jedem empfangenen Satelliten erfolgt.

Nun wird zu einem beliebigen Empfängerzeitpunkt t0* (der Empfänger wird natürlich sofort beginnen, wenn alle notwendigen Informationen eingetroffen sind) für diesen Empfängerzeitpunkt die Sendezeitpunkte aller empfangenen Satelliten berechnet.

Mit Hilfe der weiteren Informationen in den Nachrichten (Ephemeridendaten) wird für jeden Satelliten die dreidimensionale Position des Satelliten zum jeweiligen Sendezeitpunkt berechnet.

Damit ist für diesen beliebig gewählten Empfängerzeitpunkt alles Notwendige bekannt: Die Orte der Satelliten und die Sendezeitpunkte in GPS-Systemzeit und in Empfängerzeit. Die Differenz zwischen Sende- und Empfangszeitpunkt ergibt die Laufzeit, die immer noch fehlerbehaftet ist, da die Empfängeruhr nicht mit der GPS-Systemzeit synchronisiert ist. Der Zeitfehler der Empfängeruhr ist für alle Satelliten gleich und fällt deshalb bei Differenzbildungen zwischen den Sendezeitpunkten der empfangenen Satelliten heraus.

In die GPS-Grundgleichungen werden nun die 3D-Positionen der Satelliten und die Sendezeitpunkte in der GPS-Zeit eingesetzt und das Gleichungssystem gelöst. Als Ergebnis erhält man die dazugehörige Empfangszeit t0 in der GPS-Zeit und die Empfängerkoordinaten.

Damit sind alle gesuchten Sendezeitpunkte und Sendeorte bekannt.

Orts- und Zeitbestimmung des Empfängers

Mit den jetzt bekannten Sendezeitpunkten und Sendeorten der empfangenen Signale zu einem bestimmten Zeitpunkt wird der Empfängerort bestimmt. Die Uhrzeit des Empfangszeitpunkts muss weder in der GPS-Systemzeit noch in der Empfängerzeit bekannt sein. Wenn die Empfängeruhr gestellt werden soll, wird dem Empfang die Empfängeruhrzeit 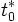$t_0^*$ zugeordnet. Dem benutzten Gleichungssystem reichen diese Daten aus, um die Empfängerkoordinaten und den Empfangszeitpunkt in der GPS-Systemzeit zu bestimmen. Die Lösung des Gleichungssystems wird im Abschnitt Die idealisierten GPS-Grundgleichungen behandelt.

Nach Lösung der GPS-Grundgleichungen hat der Empfänger seine Koordinaten (genauer die Koordinaten seiner Empfangsantenne) und den Empfangszeitpunkt t₀ in der GPS-Systemzeit. Damit kann der Empfänger prinzipiell seine Empfängeruhr mit der Differenz 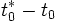$t_0^* - t_0$ auf die GPS-Systemzeit stellen (synchronisieren), aber das ist nicht notwendig. Notwendig ist es nur, wenn der GPS-Empfänger als Zeitnormal dienen soll. Da die GPS-Systemzeit nicht unbedingt genau mit der UTC-Zeit übereinstimmt, enthalten die Satellitennachrichten für diesen Zweck auch noch die Differenz zwischen UTC und GPS.

Ionosphärenkorrektur

Berücksichtigung unvermeidbarer Signalstörungen

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Die Zeit könnte theoretisch noch genauer bestimmt werden durch Auszählen der Bits in den Codeblöcken. Beim Empfangssignal geht das nicht, weil den einzelnen Chips der empfangenen Codefolge ein starkes Rauschen überlagert ist. Ursache ist die geringe Sendeleistung der Satelliten und die notwendige große Empfängerbandbreite.

Die Sendeleistung der GPS-Satelliten ist wegen der begrenzten Möglichkeiten der Energieversorgung ähnlich wie bei Fernsehsatelliten nur gering (Hälfte der Astra-Satelliten, also um die 50 Watt). Der Empfänger muss wegen der schnellen Folge der Zeichen (ca. alle μs) eine große Bandbreite haben. Deshalb hat das Empfangsignal einen so hohen Rauschanteil, dass die gesuchten Signale zum Teil im Rauschen untergehen.

Die Korrelation erfolgt deshalb in der Regel so, dass das verrauschte Signal mit der empfängereigenen Codefolge multipliziert wird. Die erforderliche Summation erfolgt mit dem multiplizierten Signal. Das ist ein Gleichsignal und deshalb kann es über eine längere Zeit summiert werden. Durch diese lange Zeit mittelt sich das Rauschen - und es bleibt nur ein kleiner Rest. Dadurch hebt sich das korrelierte Signal aus dem Rauschen heraus.

Berücksichtigung vermeidbarer Signalstörungen

Die idealisierten GPS-Grundgleichungen

Der GPS-Empfänger befindet sich an einem Ort mit den Koordinaten 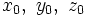$x_0,~y_0,~z_0$ und empfängt die Signale der Satelliten zur GPS-Systemzeit t₀. Die Idealisierung bezieht sich darauf, dass die Ausbreitungsgeschwindigkeit als konstant angenommen ist und die Ausbreitungsrichtung nicht gekrümmt wird.

Der Empfänger kann immer alle Satelliten gleichzeitig empfangen, da die Satelliten ununterbrochen senden. Bei Mehrkanalempfängern wird das auch so durchgeführt, bei Einkanalempfängern werden die Satelliten nacheinander empfangen, dann sind diese Zeitunterschiede beim Empfang entsprechend zur Empfangszeit zu addieren oder beim Sendezeitpunkt zu subtrahieren. Für die Berechnung des Empfangsortes werden die Empfangsdaten von mindestens 4 Satelliten benötigt. Bei mehr als 4 empfangenen Satelliten ändert sich am Rechengang wenig, allerdings sind die Gleichungen dann überbestimmt, da mehr Gleichungen als Unbekannte vorhanden sind. Gleichungssysteme mit mehr Gleichungen als Unbekannte werden in der Ausgleichsrechnung behandelt.

Die im Weiteren vorausgesetzten 4 verfügbaren Satelliten senden ihre Signale zur Systemzeit t_n an den Orten 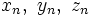$x_n,~y_n,~z_n$ aus. Dabei geht n von 1 bis 4. Das Signal breitet sich mit Lichtgeschwindigkeit c aus. Durch Gleichsetzung der Entfernungen zwischen den Satelliten und dem Empfänger in kartesichen Koordinaten und der Entfernung aus der Laufzeit, d.h. der Zeitdifferenz zwischen Sendung und Empfang multipliziert mit der Lichtgeschwindigkeit ergeben sich die Grundgleichungen. Um keine Wurzeln zu benutzen, werden die Gleichungen in Quadratform geschrieben:

$\begin{matrix} (x_1 - x_0)^2 + (y_1 - y_0)^2 + (z_1 - z_0)^2 = [c (t_1 - t_0)]^2 \quad (1)\\ (x_2 - x_0)^2 + (y_2 - y_0)^2 + (z_2 - z_0)^2 = [c (t_2 - t_0)]^2 \quad (2)\\ (x_3 - x_0)^2 + (y_3 - y_0)^2 + (z_3 - z_0)^2 = [c (t_3 - t_0)]^2 \quad (3)\\ (x_4 - x_0)^2 + (y_4 - y_0)^2 + (z_4 - z_0)^2 = [c (t_4 - t_0)]^2 \quad (4)\\ \end{matrix}$

Dieses Gleichungssystem ist zu lösen. Die Lösung liefert den Empfangszeitpunkt t₀ und die 3 Koordinaten x₀, y₀ und z₀.

Anmerkung 1: In der Literatur wird das Gleichungssystem oft mit einem Iterationsverfahren gelöst und dabei das Iterationsverfahren physikalisch interpretiert. Für t_i − t₀ wird dazu verwendet Δt_i = t_i − t₀. Die Iteration des Gleichungssystem erfolgt dann mit unterschiedlichen Startwerten. Entweder wird ein ungefährer Ort für den Empfänger angenommen und damit im ersten Iterationsschritt die Laufzeiten Δt_i für diesen Startort berechnet. Mit diesen Δt_i werden die Empfängerkoordinaten verbessert. Mit diesem verbesserten Ort werden genauere Laufzeiten bestimmt und mit diesen verbesserten Laufzeiten wieder verbesserte Koordinaten. Das zweite Iterationsverfahren nimmt als Startwert für die Laufzeiten einheitlich ca. 70 ms an. Im weiteren Berechnungsverlauf unterscheiden sich beide Iterationsverfahren nicht mehr. In der Regel ist nach 3 bis 4 Iterationen die Lösung ausreichend genau.

Anmerkung 2: Dieses Iterationsverfahren ist nicht notwendig, da, wie im folgenden gezeigt wird, auch eine geschlossene Lösung möglich ist.

Ausmultipliziert ergeben die Gleichungen (1) bis (4):

$\begin{matrix} x_1^2 - 2 x_1 x_0 + x_0^2 + y_1^2 - 2 y_1 y_0 + y_0^2 + z_1^2 - 2 z_1 z_0 + z_0^2 =\\c^2 t_1^2 - 2 c^2 t_1 t_0 + c^2 t_0^2 \qquad \qquad (5)\\ \\ x_2^2 - 2 x_2 x_0 + x_0^2 + y_2^2 - 2 y_2 y_0 + y_0^2 + z_2^2 - 2 z_2 z_0 + z_0^2 =\\c^2 t_2^2 - 2 c^2 t_2 t_0 + c^2 t_0^2 \qquad \qquad (6)\\ \\ x_3^2 - 2 x_3 x_0 + x_0^2 + y_3^2 - 2 y_3 y_0 + y_0^2 + z_3^2 - 2 z_3 z_0 + z_0^2 =\\c^2 t_3^2 - 2 c^2 t_3 t_0 + c^2 t_0^2 \qquad \qquad (7)\\ \\ x_4^2 - 2 x_4 x_0 + x_0^2 + y_4^2 - 2 y_4 y_0 + y_0^2 + z_4^2 - 2 z_4 z_0 + z_0^2 =\\c^2 t_4^2 - 2 c^2 t_4 t_0 + c^2 t_0^2 \qquad \qquad (8)\\ \end{matrix}$

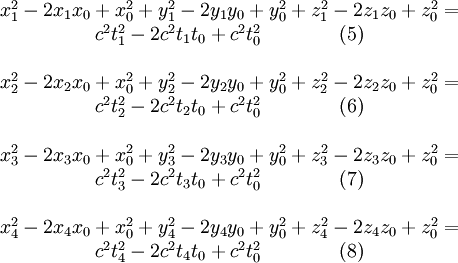
Nun wird die 4. Gleichung von den ersten 3 subtrahiert. Dadurch fallen alle quadratischen Unbekannten weg: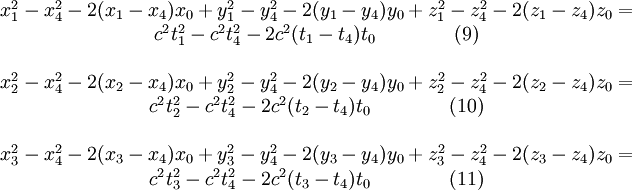

$\begin{matrix} x_1^2-x_4^2-2(x_1-x_4) x_0 + y_1^2 - y_4^2 - 2(y_1-y_4)y_0 + z_1^2 - z_4^2 - 2(z_1-z_4)z_0 =\\c^2 t_1^2 - c^2 t_4^2 - 2 c^2(t_1-t_4)t_0 \qquad \qquad (9)\\ \\ x_2^2-x_4^2-2(x_2-x_4) x_0 + y_2^2 - y_4^2 - 2(y_2-y_4)y_0 + z_2^2 - z_4^2 - 2(z_2-z_4)z_0 =\\c^2 t_2^2 - c^2 t_4^2 - 2 c^2(t_2-t_4)t_0 \qquad \qquad (10)\\ \\ x_3^2-x_4^2-2(x_3-x_4) x_0 + y_3^2 - y_4^2 - 2(y_3-y_4)y_0 + z_3^2 - z_4^2 - 2(z_3-z_4)z_0 =\\c^2 t_3^2 - c^2 t_4^2 - 2 c^2(t_3-t_4)t_0 \qquad \qquad (11)\\ \end{matrix}$

Umgeordnet wird daraus: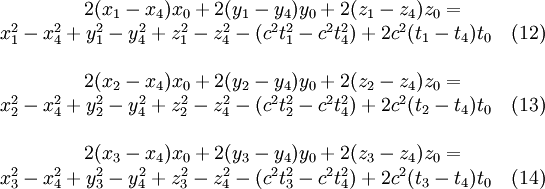

$\begin{matrix} 2(x_1-x_4) x_0 + 2(y_1-y_4)y_0 + 2(z_1-z_4)z_0 =\\x_1^2-x_4^2 + y_1^2 - y_4^2 + z_1^2 - z_4^2 - (c^2 t_1^2 - c^2 t_4^2) + 2 c^2(t_1-t_4)t_0 \quad (12)\\ \\ 2(x_2-x_4) x_0 + 2(y_2-y_4)y_0 + 2(z_2-z_4)z_0 =\\x_2^2-x_4^2 + y_2^2 - y_4^2 + z_2^2 - z_4^2 - (c^2 t_2^2 - c^2 t_4^2) + 2 c^2(t_2-t_4)t_0 \quad (13)\\ \\ 2(x_3-x_4) x_0 + 2(y_3-y_4)y_0 + 2(z_3-z_4)z_0 =\\x_3^2-x_4^2 + y_3^2 - y_4^2 + z_3^2 - z_4^2 - (c^2 t_3^2 - c^2 t_4^2) + 2 c^2(t_3-t_4)t_0 \quad (14)\\ \end{matrix}$

Durch die Reduktion auf 3 Gleichungen für immer noch 4 Unbekannte ist dieses Gleichungssystem zunächst unterbestimmt. Es lässt sich daher interpretieren als funktionale Abhängigkeit der gesuchten Koordinaten von einer Variablen t₀. Da es sich um ein lineares Gleichungssystem handelt, ist auch diese Abhängigkeit linear, d. h. sie hat die Form

$\begin{matrix} x_0 = x_{00} + x_{0t} t_0&amp;amp; &amp;amp;y_0 = y_{00} + y_{0t} t_0&amp;amp; &amp;amp;z_0 = z_{00} + z_{0t} t_0 \qquad (15)\\ \end{matrix}$

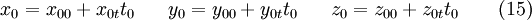
mit entsprechenden Konstanten x₀₀ , x_0t usw. Setzt man diese Ausdrücke in die 3 Gleichungen ein, und eliminiert damit die gesuchten Koordinaten, so enthalten sie außer der Variablen t₀ nur noch konstante Größen. Diese 3 Gleichungen müssen daher für die konstanten Terme und die Vorfaktoren von t₀ separat gelten. Man erhält damit die beiden Gleichungssysteme

$\begin{matrix} 2(x_1-x_4) x_{00} + 2(y_1-y_4)y_{00} + 2(z_1-z_4)z_{00} =\\x_1^2-x_4^2 + y_1^2 - y_4^2 + z_1^2 - z_4^2 - (c^2 t_1^2 - c^2 t_4^2) \qquad \qquad (16)\\ \\ 2(x_2-x_4) x_{00} + 2(y_2-y_4)y_{00} + 2(z_2-z_4)z_{00} =\\x_2^2-x_4^2 + y_2^2 - y_4^2 + z_2^2 - z_4^2 - (c^2 t_2^2 - c^2 t_4^2) \qquad \qquad (17)\\ \\ 2(x_3-x_4) x_{00} + 2(y_3-y_4)y_{00} + 2(z_3-z_4)z_{00} =\\x_3^2-x_4^2 + y_3^2 - y_4^2 + z_3^2 - z_4^2 - (c^2 t_3^2 - c^2 t_4^2) \qquad \qquad (18)\\ \\ 2(x_1-x_4) x_{0t} + 2(y_1-y_4)y_{0t} + 2(z_1-z_4)z_{0t} = 2 c^2(t_1-t_4) \qquad (19)\\ 2(x_2-x_4) x_{0t} + 2(y_2-y_4)y_{0t} + 2(z_2-z_4)z_{0t} = 2 c^2(t_2-t_4) \qquad (20)\\ 2(x_3-x_4) x_{0t} + 2(y_3-y_4)y_{0t} + 2(z_3-z_4)z_{0t} = 2 c^2(t_3-t_4) \qquad (21)\\ \end{matrix}$

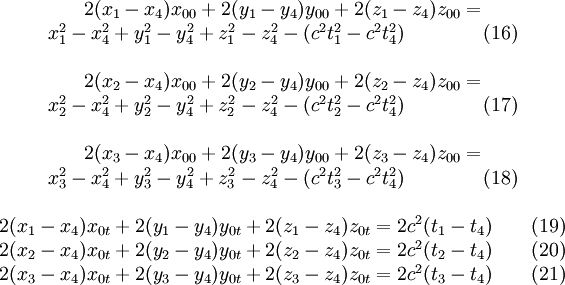
Es handelt sich um 2 lineare Gleichungssysteme mit der gleichen Koeffizientenmatrix. Ihre Lösungen werden nun in eine der Ausgangsgleichungen eingesetzt. Damit wird nach der Reduktion auf 3 Gleichungen wieder eine vierte davon unabhängige hinzugenommen, und damit die vorübergehende Unterbestimmheit behoben. Man erhält z. B. durch Einsetzen in die vierte Ausgangsgleichung

$\begin{matrix} (x_4 - x_{00} - x_{0t} t_0)^2 + (y_4 - y_{00} - y_{0t} t_0)^2 + (z_4 - z_{00} - z_{0t} t_0)^2 = [c (t_4 - t_0)]^2\\ \end{matrix}$

Die Terme werden ausmultipliziert und nach Potenzen von t₀ geordnet:

$\begin{matrix} A := (x_4 - x_{00})^2 + (y_4 - y_{00})^2 + (z_4 - z_{00})^2 - [c t_4]^2\\ B := (x_4 - x_{00}) x_{0t} + (y_4 - y_{00}) y_{0t} + (z_4 - z_{00}) z_{0t} - c^2 t_4\\ C := x_{0t}^2 + y_{0t}^2 + z_{0t}^2 - c^2\\ \end{matrix}$

Mit den Konstanten A,B und C ergibt sich eine quadratische Gleichung für t₀

$C t_0^2 - 2 B t_0 + A = 0$

mit den zwei Lösungen:

$t_0 = \frac{B \pm \sqrt{B^2 - A C}}{C}$

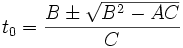
Bei realistischen Ausgangsdaten ergeben sich stets zwei reelle Lösungen. Eine davon scheidet als unrealistisch aus, entweder weil sie vor den Sendezeitpunkten der Satelliten liegt oder zu Positionen führt, die oberhalb der Satellitenbahnen liegen. Damit sind alle Werte bekannt, um die Koordinaten anzugeben.

$\begin{matrix} x_0 = x_{00} + x_{0t} t_0&amp;amp; &amp;amp;y_0 = y_{00} + y_{0t} t_0&amp;amp; &amp;amp;z_0 = z_{00} + z_{0t} t_0\\ \end{matrix}$

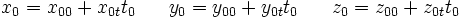
Die Winkel der Verbindungslinien zwischen dem zu vermessenden Punkt und den Referenzpunkten muss möglichst groß sein. Sind die Winkel zu klein, ist eine exakte Positionsbestimmung nicht möglich.