Ganzheit (Kommutative Algebra)
- Ganzheit (Kommutative Algebra)
-
Im mathematischen Teilgebiet der kommutativen Algebra ist Ganzheit eine leichte Abwandlung des Begriffes eines algebraischen Elementes, die aber wesentlich andere Eigenschaften bewirkt.
Definition
Es sei A ein Ring und B eine A-Algebra. Dann heißt ein Element 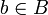 ganz über A, wenn es ein normiertes Polynom
ganz über A, wenn es ein normiertes Polynom
![p=X^n+c_{n-1}X^{n-1}+\ldots+c_1X+c_0\in A[X]](/pictures/dewiki/98/b87c961d9679e6a9e1f098081357fed5.png)
gibt, so dass
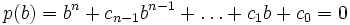
gilt.
B heißt ganz über A, wenn jedes Element von B ganz über A ist. Ist insbesondere 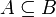 , so spricht man von einer ganzen Ringerweiterung.
, so spricht man von einer ganzen Ringerweiterung.
Für eine beliebige A-Algebra B heißt die Menge der über A ganzen Elemente von B der ganze Abschluss von A in B.
Eigenschaften
- Der ganze Abschluss von A in B ist eine A-Unteralgebra von B.
Beispiele
- Ist
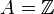 und
und 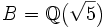 , so ist der ganze Abschluss von A in B gleich
, so ist der ganze Abschluss von A in B gleich
-
![\mathbb Z\!\left[\frac{1+\sqrt5}2\right].](/pictures/dewiki/102/f632f6672eab286873f00dfeea28628f.png)
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Ganzheit (kommutative Algebra) — Im mathematischen Teilgebiet der kommutativen Algebra ist Ganzheit eine leichte Abwandlung des Begriffes eines algebraischen Elementes, die aber wesentlich andere Eigenschaften bewirkt. Definition Es sei A ein Ring und B eine A Algebra. Dann… … Deutsch Wikipedia
Ganzheit — ist ein Fachbegriff in folgenden Fachgebieten: in der Mathematik, siehe Ganzheit (kommutative Algebra) in der Philosophie, siehe Ganzheit (Philosophie) In der Alltagssprache wird das Wort Ganzheit auch für Ganzheitlichkeit verwendet … Deutsch Wikipedia
Adjunktion (Algebra) — Unter Adjunktion versteht man im mathematischen Teilgebiet der Algebra das Hinzufügen von weiteren Elementen zu einem Körper oder Ring. Inhaltsverzeichnis 1 Adjunktion algebraischer Elemente zu einem Körper 2 Adjunktion transzendenter Elemente zu … Deutsch Wikipedia
Ganzalgebraische Zahl — In der Mathematik ist eine algebraische Zahl x eine reelle oder komplexe Zahl, die Nullstelle eines Polynoms vom Grad größer als Null mit rationalen Koeffizienten ak k=0,...,n ist; also Lösung der Gleichung f(x) = 0. Die so definierten… … Deutsch Wikipedia
Algebraische Zahl — In der Mathematik ist eine algebraische Zahl x eine reelle oder komplexe Zahl, die Nullstelle eines Polynoms vom Grad größer als Null mit rationalen Koeffizienten ist, also Lösung der Gleichung f(x) = 0. Die so definierten algebraischen Zahlen… … Deutsch Wikipedia
Normal (Mathematik) — Das Wort normal wird in der Mathematik in den folgenden Zusammenhängen benutzt: in der Geometrie: orthogonal in der Algebra: in der Gruppentheorie sagt man, eine Untergruppe sei normal, wenn sie ein Normalteiler ist in der Körpertheorie für… … Deutsch Wikipedia
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Euklidisch — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Fehlstand — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Integrabel — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
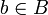 ganz über A, wenn es ein normiertes Polynom
ganz über A, wenn es ein normiertes Polynom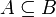 , so spricht man von einer ganzen Ringerweiterung.
, so spricht man von einer ganzen Ringerweiterung.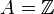 und
und 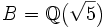 , so ist der ganze Abschluss von A in B gleich
, so ist der ganze Abschluss von A in B gleich
![p=X^n+c_{n-1}X^{n-1}+\ldots+c_1X+c_0\in A[X]](/pictures/dewiki/98/b87c961d9679e6a9e1f098081357fed5.png)
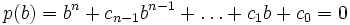
![\mathbb Z\!\left[\frac{1+\sqrt5}2\right].](/pictures/dewiki/102/f632f6672eab286873f00dfeea28628f.png)