Gauß'sches Integral

Das gaußsche Fehlerintegral (nach Carl Friedrich Gauß) wird auch Wahrscheinlichkeitsverteilungsfunktion Φ genannt. Es ist das Integral von 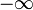$-\infty$ bis z über die Normalverteilung (hier mit μ = 0 und σ = 1). Da die gesamte Fläche unterhalb der Normalverteilung (auch Gauß-Glocke genannt) 1 ist, ist der Wert des Fehlerintegrals für 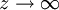$z\rightarrow\infty$ ebenfalls 1 (siehe Abschnitt Normierung). Das Fehlerintegral ist durch

$\Phi(z)=\frac 1{\sqrt{2\pi}} \int_{-\infty}^z e^{-\frac 12 t^2} \mathrm dt$

definiert.

Lässt man das Integral erst bei 0 statt bei 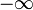$-\infty$ beginnen, so spricht man von Φ₀:

$\Phi_0(z)=\frac 1{\sqrt{2\pi}} \int_0^z e^{-\frac 12 t^2} \mathrm dt = \Phi(z)-\frac 12.$

Zusammenhang zur gaußschen Fehlerfunktion

Durch Substitution der o.g. Formeln 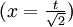$(x=\tfrac t{\sqrt 2})$ und durch passende Umformungen lässt sich aus Φ bzw. Φ₀ die Fehlerfunktion

$\operatorname{erfc}(z) = 2 \left(1-\Phi(\sqrt 2z)\right)$

bzw.

$\operatorname{erf}(z) = 2 \Phi_0(\sqrt 2z)$

herleiten.

Anwendung

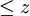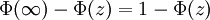Das Fehlerintegral gibt an zu welcher Wahrscheinlichkeit ein Wert $\le z$ in einem gaußverteilten stochastischen Prozess (mit μ = 0, σ = 1) enthalten ist. Umgekehrt kann auch die Wahrscheinlichkeit für einen Wert $\ge z$ ermittelt werden, indem man $\Phi(\infty)-\Phi(z)=1-\Phi(z)$ bildet.

Als elektrotechnisches Beispiel sei ein gaußverteiltes Störrauschen der Streuung σ = 1,25V angenommen das einem Übertragungskanal überlagert ist. Dieser Kanal arbeite fehlerfrei, solange die Störungen im Bereich -5V...+5V liegen. Es klärt sich nun schnell die Frage, wie wahrscheinlich eine fehlerhafte Übertragung ist:

Wahrscheinlichkeit für einen Rauschwert $\le -5\mathrm V$:

$p_1 = \Phi(-5\mathrm V/\sigma) = \Phi(-4) = 0{,}317 \cdot 10^{-4}.$

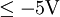Wahrscheinlichkeit für einen Rauschwert $\ge +5\mathrm V$:

$p_2 = \Phi(\infty) - \Phi(5\mathrm V/\sigma) = 1-\Phi(4) = 0{,}317 \cdot 10^{-4}.$

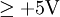Die Gesamtwahrscheinlichkeit für einen Übertragungsfehler ergibt sich dann aus p = p₁ + p₂

Normierung

Die Normierung lässt sich wie folgt nachweisen:

Wir definieren

$A := \lim_{z \to \infty} \Phi(z) = \frac 1{\sqrt{2\pi}} \int_{-\infty}^\infty e^{-\frac 12 t^2}\mathrm dt.$

Ist die Verteilung Φ normiert, so muss A = 1 gelten.

Es gilt

$A = \frac 1{\sqrt{2\pi}} I,$

wobei

$I := \int_{-\infty}^\infty e^{-\frac 12 t^2}\mathrm dt.$

Dieses unbestimmte Integral ist nach wie vor nicht elementar zu integrieren. Der entscheidende Trick für die Berechnung (angeblich von Poisson) ist, nun auf eine höhere Dimension auszuweichen und das resultierende 2D-Integrationsgebiet anders zu parametrisieren:

$\begin{align} I^2 &= \left(\int_{-\infty}^\infty e^{-\frac 12 x^2}\mathrm dx\right)\left(\int_{-\infty}^\infty e^{-\frac 12 y^2}\mathrm dy\right)\\ &= \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-\frac 12 x^2}e^{-\frac 12 y^2}\mathrm dx\,\mathrm dy\\ &= \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-\frac 12 \left(x^2 + y^2\right)}\mathrm dx\,\mathrm dy. \end{align}$

Grundlage für die erste Umformung ist die Linearität des Integrals.

Statt längs kartesischer Koordinaten wird über $\R^2$ nun längs Polarkoordinaten integriert, was der Substitution r² = x² + y² entspricht und man erhält schließlich

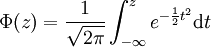
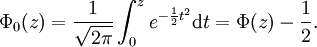
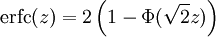
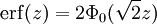
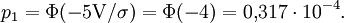
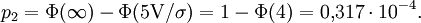
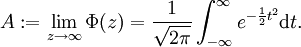
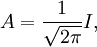
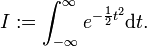
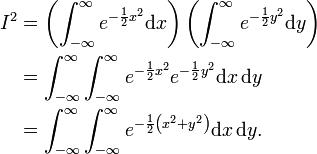
$\begin{align} I^2 &= \int_0^\infty \int_0^{2\pi} e^{-\frac 12 r^2} r\,\mathrm d\varphi\,\mathrm dr\\ &= 2 \pi \int_0^\infty e^{-\frac 12 r^2} r\,\mathrm dr\\ &= -2 \pi \left[e^{-\frac 12 r^2}\right]_0^{r \to \infty}\\ &= 2 \pi. \end{align}$

siehe auch: Tabelle Standardnormalverteilung