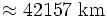- Geostationärer Orbit
-
Eine geosynchrone Umlaufbahn ist ein Satellitenorbit mit einer Umlaufzeit um die Erde, die der Rotationsdauer der Erde um ihre eigene Achse (23 Stunden, 56 Minuten, 4,09 Sekunden = 1 siderischer Tag) entspricht. Seine Bodenspur auf der Erde ist eine geschlossene Kurve (Analemma), bei einem ideal geostationären Satelliten ein Punkt.
Inhaltsverzeichnis
Orbitklassen
Geneigter Orbit
Geosynchrone Umlaufbahnen besitzen eine Inklinationswinkel zwischen 0° (geostationär) über 90° (Polarbahn) bis 180° (Gegenläufigkeit zur Erddrehung) und heißen geneigter geosynchroner Orbit, englisch Inclined geosynchronous orbit (IGSO). Die große Halbachse der Umlaufbahn beträgt immer 42157 km.
Geneigte Umlaufbahnen mit geringer Bahnneigung werden unter dem Namen Inclined-Orbit von vormaligen geostationären Nachrichtensatelliten benutzt um ihre Lebensdauer bei fast erschöpften Treibstoffreserven zu verlängern. Weil dann jedoch ihre Position am Himmel schwankt, sind solche Satelliten nur noch mit professionellen Antennen mit Antennennachführung empfangbar.
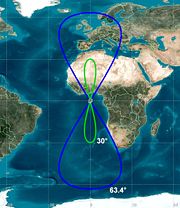
Kreisförmige Orbits großer Inklination heißen auch Tundra-Orbits. Vier äquidistant platzierte Satelliten mit einer Inklination von 63.4° decken die gesamte Erde ab.
Ist die Bahn zusätzlich exzentrisch, nennt man sie 24h-Molnija-Orbit -- im Unterschied zu 12h- oder 6h-Molnija-Orbits mit entsprechend kürzeren nichtsynchronen Umlaufzeiten.
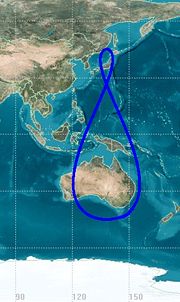
Das Quasi-Zenith Satellite System (QZSS) bezeichnet ein System aus drei Satelliten, das für die Verbesserung des GPS-Empfangs in Japan geplant war. Satelliten auf einer 45° geneigten Bahn, einer Exzentrizität von 0,09 und einem Perigäumswinkel (Argument des Perigäums) von 270° stehen für acht Stunden fast senkrecht über der Insel.
Geostationärer Orbit
 Ausleuchtzone eines geostationären Satelliten
Ausleuchtzone eines geostationären SatellitenDer Sonderfall einer kreisförmigen Umlaufbahn, deren Bahnneigung Null ist, und die in Richtung nach Osten orientiert ist, heißt geostationär. Die Bahngeschwindigkeit beträgt dabei stets 3075 Meter pro Sekunde (11.070 km/h), der Bahnradius 42157 km, was einem Abstand von etwa 35786 km über der Erdoberfläche entspricht.
Von der Erde aus betrachtet scheint ein geostationärer Satellit am Himmel still zu stehen, da sich der Beobachter auf der Erde mit der gleichen Winkelgeschwindigkeit bewegt wie der Satellit. Deswegen wird diese Umlaufbahn häufig für Fernseh- und Kommunikationssatelliten verwendet. Die Antennen auf dem Boden sind fest auf einen bestimmten Punkt ausgerichtet und jeder Satellit deckt stets das gleiche Gebiet der Erde ab.
Im 1928 erschienenen Buch Das Problem der Befahrung des Weltraums – der Raketenmotor von Herman Potočnik findet sich die erste Veröffentlichung dieser Idee.
Formeln
Um einen Körper der Masse m mit der Winkelgeschwindigkeit ω auf einer Kreisbahn mit dem Radius r zu halten, ist eine Zentripetalkraft der Stärke
- F1 = mω2r
erforderlich. Auf einer Kreisbahn um einen Planeten ist die Schwerkraft (näherungsweise) die einzig wirkende Kraft. Im Abstand r – vom Mittelpunkt des Planeten ausgehend – kann sie mit der Formel
berechnet werden. Dabei bezeichnet G die Gravitationskonstante und M die Masse des Planeten.
Da die Schwerkraft also die einzige Kraft ist, die den Körper auf der Kreisbahn hält, muss ihr Wert der Zentripetalkraft entsprechen. Es gilt also:
- F1 = F2
Es ergibt sich durch Einsetzen:
Auflösen nach r ergibt:
Die Kreisfrequenz ω ergibt sich aus der Umlaufdauer t als:
Einsetzen in die Formel für r ergibt:
Diese Formel bestimmt nun den Radius der geostationären Umlaufbahn eines Massenschwerpunktes vom Mittelpunkt des betrachteten Planeten ausgehend. Um die Entfernung der Bahn von der Oberfläche des Planeten – also beispielsweise die Höhe eines geostationären Satelliten über der Erdoberfläche – zu erhalten, muss dessen Radius vom Ergebnis subtrahiert werden. Somit haben wir einfach:
wobei RP den Radius des Planeten bezeichnet.
Für einen geostationären Mond oder ein anderes Objekt, welches selbst eine gewisse Ausdehnung besitzt, ist die obige Formel dieselbe; um jedoch den Abstand von der Oberfläche eines Planeten zu der Oberfläche eines solchen Mondes zu erhalten, muss zusätzlich zu dem Radius des Planeten noch der Radius des Mondes subtrahiert werden. Ganz allgemein gilt also:
wobei RM den Radius des Mondes bezeichnet.
Berechnung
Aus
ergibt sich
Die Formel lautet also
oder
Für die Erde mit der ungefähren Erdmasse M = 5,9736 · 1024 kg und der Rotationsdauer, also näherungsweise 23 Stunden, 56 Minuten, 4,09 Sekunden = (23 · 60 + 56) · 60 + 4,09 Sekunden = 86164,09 Sekunden gilt:
vom Erdmittelpunkt. Abzüglich des Erdradiuses
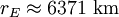 also
also 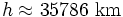 von der Erdoberfläche entfernt.
von der Erdoberfläche entfernt.Geschichte
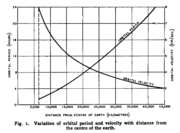
Im Jahr 1945 schlug der Science-Fiction-Autor Arthur C. Clarke vor, Satelliten auf einer geostationären Umlaufbahn zu positionieren. Mit drei Satelliten, jeweils um 120° versetzt, wäre eine Radiokommunikation weltweit möglich. Er nahm an, dass innerhalb der nächsten 25 Jahre Satelliten dort positioniert werden könnten. Mit Syncom 2 in der Geosynchronen- und Syncom 3 in der Geostationären Umlaufbahn wurde seine Idee im Jahr 1963 und 1964 nach nur ca. 19 Jahren verwirklicht.
Das Bild rechts zeigt das Diagramm, in dem Clarke seine Überlegungen in der Zeitschrift Wireless World zum ersten Mal der Öffentlichkeit vorstellte [1].
Siehe auch
Quellen
Weblinks
Wikimedia Foundation.

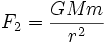
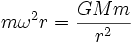
![r = \sqrt[3]{G \frac{M}{\omega^2}}](/pictures/dewiki/102/f191ca3c51b89d1bb16d932de3c6de32.png)
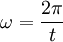
![r = \sqrt[3]{\frac{G}{4 \pi^2} M t^2}](/pictures/dewiki/98/bc26efa930340ab682dbf013501eb4cd.png)
![h = \sqrt[3]{\frac{G}{4 \pi^2} M t^2} - R_P](/pictures/dewiki/57/9f8cd32f8d6aec86b0e107ce4584bd55.png)
![h = \sqrt[3]{\frac{G}{4 \pi^2} M t^2} - (R_P + R_M)](/pictures/dewiki/98/b766f492f935703622573b4842773201.png)
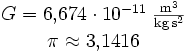
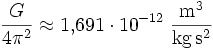
![r \approx \sqrt[3]{1{,}691\cdot10^{-12}\;\mathrm{\frac{m^3}{kg\,s^2}}\quad M t^2}](/pictures/dewiki/52/4e69125dedb094251fcd599bce2a6c47.png)
![r \approx 1{,}191\cdot10^{-4}\
\sqrt[3]{1\ \mathrm{\frac{m^3}{kg\,s^2}}\quad M t^2}](/pictures/dewiki/52/4c0a4dd8d54f7a813ed0162216ab0324.png)
![r \approx 1{,}191 \cdot 10^{-4}\
\sqrt[3]{
1\ \mathrm{\frac{m^3}{kg\,s^2}}
\quad 5{,}9736 \cdot 10^{24}\ \mathrm{kg}
\ (86164{,}09\ \mathrm{s})^2
}](/pictures/dewiki/98/bb6d475dcddc594f314eb223baaae6a2.png)