- Grellingsche Paradoxie
-
Die Grelling-Nelson-Antinomie ist ein semantisches Paradoxon, das 1908 von Kurt Grelling und Leonard Nelson als Variante der Russellschen Antinomie formuliert wurde.
Charakterisierung und Problematik
Grelling und Nelson gehen bei der Bildung ihrer Antinomie davon aus, dass jede Menge durch ein Merkmal definiert ist, das ein Wort bezeichnet. Zum Beispiel bezeichnet das Wort „einsilbig“ das Merkmal der Menge aller einsilbigen Wörter. Sie zerlegen dann die Wörter in zwei Klassen, die folgendermaßen definiert sind:
- Ein autologisches Wort besitzt selbst das Merkmal, das es bezeichnet, ein heterologisches Wort dagegen nicht.
Die Wörter „deutsch“ oder „dreisilbig“ sind autologisch, denn „deutsch“ ist ein deutsches Wort und „dreisilbig“ ein dreisilbiges Wort. Die meisten Wörter sind aber heterologisch, zum Beispiel „englisch“ und „einsilbig“, denn „englisch“ ist kein englisches Wort und „einsilbig“ kein einsilbiges Wort. Dagegen scheitert der Versuch, das Wort „heterologisch“ in diese beiden Klassen einzuordnen, an einem Widerspruch:
- Angenommen „heterologisch“ ist ein autologisches Wort, dann ist es laut Definition ein heterologisches Wort im Widerspruch zur Annahme. Angenommen es trifft das Gegenteil zu und „heterologisch“ ist ein heterologisches Wort, dann ist es laut Definition kein heterologisches Wort, also ist es autologisch im Widerspruch zur Annahme.
Lösungen
Grelling und Nelson übertrugen in ihrer Antinomie die Russellsche Antinomie auf die Sprachebene, indem sie jeder Menge ein Wort als Namen zuordneten durch eine umkehrbar eindeutige Funktion
 ; dabei entspricht der Russellschen Klasse die Klasse der heterologischen Wörter
; dabei entspricht der Russellschen Klasse die Klasse der heterologischen Wörter 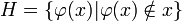 , so dass
, so dass 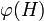 das Wort „heterologisch“ bezeichnet. [1] Daher ist die Lösung der Grelling-Nelson-Antinomie völlig parallel zur Lösung der Russellschen Antinomie: Man kann beweisen, dass die Klasse
das Wort „heterologisch“ bezeichnet. [1] Daher ist die Lösung der Grelling-Nelson-Antinomie völlig parallel zur Lösung der Russellschen Antinomie: Man kann beweisen, dass die Klasse 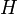 aller heterologischen Wörter keine Menge ist, sondern eine sogenannte echte Klasse.
aller heterologischen Wörter keine Menge ist, sondern eine sogenannte echte Klasse.Die Grelling-Nelson-Antinomie hat damit folgende logische Konsequenz: Da jede übliche Sprache durch eine Wortmenge über einem Alphabet beschrieben werden kann, bedeutet sie, dass nicht alle Mengen durch ein Wort benannt werden können. Dazu wäre eine echte Klasse von Worten nötig, die mit einem endlichen Alphabet nicht erzeugt werden kann. Weil diese sprachlichen Voraussetzungen der Antinomie nicht gegeben sind, wird sie zu den sogenannten semantischen Paradoxien gezählt.
Bei der Lösung in der ungebräuchlicheren und komplizierteren verzweigten Typentheorie werden dagegen die Sprachebenen strikt getrennt und die Syntax so eingeschränkt, dass die Aussagen
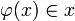 und
und 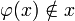 syntaktisch nicht mehr korrekt sind und die beiden Wortklassen gar nicht mehr gebildet und definiert werden können.
syntaktisch nicht mehr korrekt sind und die beiden Wortklassen gar nicht mehr gebildet und definiert werden können.Literatur
K. Grelling und L. Nelson: Bemerkungen zu den Paradoxien von Russell und Burali-Forti. In: Abhandlungen der Fries’schen Schule II, Göttingen 1908, S. 301-334.
- ↑ Grelling/Nelson S. 307: „Sei φ(M) dasjenige Wort, das den Begriff bezeichnet, durch den M definiert ist. Dieses Wort ist entweder Element von M oder nicht. Im ersten Falle wollen wir es „autologisch“ nennen, im anderen „heterologisch“.“ Nach Grelling/Nelson S. 306 ist hier φ als bijektive, umkehrbar eineindeutige Funktion vorausgesetzt.
Wikimedia Foundation.
