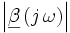- Großsignal-Ersatzschaltbild
-
Um das Verhalten eines Bipolartransistors oder Feldeffekttransistors auch in komplexen Schaltungen berechnen zu können, benötigt man ein vereinfachtes, abstraktes, Modell. Hierbei werden verschiedene Stufen der Abstraktion verwendet. Hierbei werden meist einfache Modelle zur Dimensionierung und komplexere Modelle bzw. deren Ersatzschaltbild zur Schaltungssimulation verwendet.
Theoretisch wäre auch eine exakte Berechnung des physikalischen Verhaltens beispielsweise über eine Monte-Carlo-Simulation möglich, aber schon in relativ einfachen elektrischen Netzwerken übersteigt der Rechenaufwand einer solchen Simulation die Leistung heutiger Computer. Die Modelle dienen daher zur Vereinfachung und hinreichenden Nachbildung der realen Abläufe, um so den Rechenaufwand drastisch zu reduzieren.
Eine weitere Vereinfachung kann durch die Nutzung unterschiedlicher Modelle für den statischen und den dynamischen Betrieb erreicht werden. Erstere dienen zur gleichstrommäßigen Dimensionierung, und damit vor allem zur Berechnung der korrekten Arbeitspunkteinstellung, sowie für niederfrequente Logikschaltungen (z. B. TTL). Modelle für den dynamischen Betrieb dienen der wechselstrommäßigen Dimensionierung und damit zur Berechnung von Schaltungen für die Signalübertragung und Signalverarbeitung.
Der vorliegende Artikel beschäftigt sich ausschließlich mit der Modellierung des Bipolartransistors, für Informationen über den Aufbau und die Verwendung von Bipolartransistoren wird auf den Hauptartikel verwiesen.
Inhaltsverzeichnis
- 1 Formelzeichen
- 2 Modelle für das statische Verhalten
- 3 Modelle für das dynamische Verhalten
- 4 Literatur
- 5 Fußnoten und Einzelnachweise
Formelzeichen
Im Folgenden werden die hier verwendeten Formelzeichen aufgelistet. Für weitere Formelzeichen siehe auch die mathematische Beschreibung.
Zeichen Beschreibung IB,N Idealer Basisstrom der Emitter-Diode IB,I Idealer Basisstrom der Kollektor-Diode IB,E Basis-Leckstrom der Emitter-Diode IB,C Basis-Leckstrom der Kollektor-Diode IT Kollektor-Emitter Transportstrom ID,S Strom der Substrat-Diode RB Basiswiderstand RC Kollektorbahnwiderstand RE Emitterwiderstand CS,E Sperrschichtkapazität der Emitter-Diode CS,Ci Interne Sperrschichtkapazität der Kollektor-Diode CS,Ce Externe Sperrschichtkapazität der Kollektor-Diode CS,S Sperrschichtkapazität der Substrat-Diode CD,N Diffusionskapazität der Emitter-Diode CD,I Diffusionskapazität der Kollektor-Diode Formelzeichen für das statische und dynamische Verhalten
Formelzeichen für das statische Verhalten Zeichen Beschreibung IS Sättigungssperrstrom IS,S Sättigungssperrstrom der Substrat-Diode BN Ideale Stromverstärkung im Normalbetrieb BI Ideale Stromverstärkung im Inversbetrieb IS,E Leck-Sättigungssperrstrom der Emitter-Diode IS,C Leck-Sättigungssperrstrom der Kollektor-Diode nE Emissionskoeffizient der Emitter-Diode nC Emissionskoeffizient der Kollektor-Diode IK,N Kniestrom zur starken Injektion im Normalbetrieb IK,I Kniestrom zur starken Injektion im Inversbetrieb UA,N Early-Spannung im Normalbetrieb UA,I Early-Spannung im Inversbetrieb RBe Externer Bahnwiderstand RBi Interner Bahnwiderstand1) 1) wird in PSpice aus der Gleichung RB = RBe + RBi berechnet. Formelzeichen für das dynamische Verhalten Zeichen Beschreibung CS0,E Null-Kapazität der Emitter-Diode CS0,C Null-Kapazität der Kollektor-Diode CS0,S Null-Kapazität der Substrat-Diode Udiff,E Diffusionsspannung der Emitter-Diode Udiff,C Diffusionsspannung der Kollektor-Diode Udiff,S Diffusionsspannung der Substrat-Diode mS,E Kapazitätskoeffizient der Emitter-Diode mS,C Kapazitätskoeffizient der Kollektor-Diode mS,S Kapazitätskoeffizient der Substrat-Diode xCSC Aufteilungskoeffizient der Kapazität in der Kollektor-Diode fS Koeffizient für den Kapazitätsverlauf τ0,N Ideale Transitzeit im Normalbetrieb τ0,I Ideale Transitzeit im Inversbetrieb xτ,N Transitzeitkoeffizient im Normalbetrieb xτ,I Transitzeitkoeffizient im Inversbetrieb Uτ,N Transitzeitspannung im Normalbetrieb Uτ,I Transitzeitspannung im Inversbetrieb Uτ,N Transitzeitstrom im Normalbetrieb Uτ,I Transitzeitstrom im Inversbetrieb Weitere Formelzeichen
Formelzeichen für das thermische Verhalten Zeichen Beschreibung xT,I Temperaturkoeffizient der Sperrströme xT.B Temperaturkoeffizient der Stromverstärkung Englische Bezeichnung
Da Datenblätter meist in englisch verfasst sind, muss man auch die verwendeten Formelzeichen übersetzen können. Im Wesentlichen sind dies:
Deutsch Englisch Bezeichnung Zeichen Bezeichnung Zeichen Spannung U voltage V Normalbetrieb N forward region F Inversbetrieb I inverse region R Sperrschicht S junction J Die anderen Bezeichnungen können beibehalten werden.
Modelle für das statische Verhalten
Ebers-Moll-Modell
Das Ebers-Moll-Modell ist das einfachste Modell für den Bipolartransistor. Es hat nur drei Parameter und beschreibt damit die wichtigsten Effekte. Das Ebers-Moll-Modell wird mit Hilfe eines Dioden-Ersatzschaltbildes dargestellt.
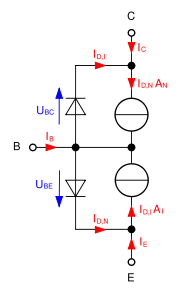
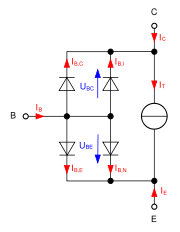
Ein npn-Transistor besteht aus zwei antiseriellen pn-Übergängen (Dioden) mit gemeinsamer p-Zone. Diese Übergänge werden als Emitter-Diode (Basis-Emitter-Diode; BE-Diode) und Kollektor-Diode (Basis-Kollektor-Diode; BC-Diode) bezeichnet. Durch die dünne Basis (p-Zone) im Bipolartransistor fließt der Großteil des Stromes über den Emitter ab. Daher besteht das Ebers-Moll-Modell zusätzlich zu den beiden Dioden aus zwei Stromquellen, die den Stromfluss durch die Basis beschreiben. Für den pnp-Transistor werden einfach die Vorzeichen umgedreht.
Zusätzlich wird noch ein Steuerfaktor für den Normalbetrieb
 sowie den Inversbetrieb
sowie den Inversbetrieb  verwendet, um den unsymmetrischen Aufbau eines realen npn-Transistors zu berücksichtigen.
verwendet, um den unsymmetrischen Aufbau eines realen npn-Transistors zu berücksichtigen.Im Normalbetrieb sperrt die BC-Diode da UBC < 0 und kann deshalb vernachlässigt werden. Zusätzlich kann die zugehörige Exponentialfunktion durch -1 ersetzt werden, da
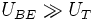 ist. Umgekehrt sperrt im Inversbetrieb die BE-Diode, wodurch man auch in diesem Fall eine Vereinfachung der Geichung auf dieselbe Weise erhält.
ist. Umgekehrt sperrt im Inversbetrieb die BE-Diode, wodurch man auch in diesem Fall eine Vereinfachung der Geichung auf dieselbe Weise erhält.Reduzierte Ebers-Moll-Modelle für den npn-Transistor Normalbetrieb Inversbetrieb _svg.png)
_svg.png)



mit 
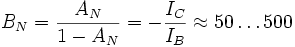
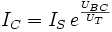

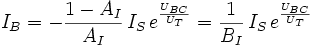
mit 
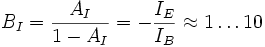
Ebers-Moll-Modell im Sättigungsbetrieb
Wenn man den Bipolartransistor als Schalter einsetzt, kommt dieser vom Normalbetrieb in den Sättigungsbetrieb. Hierbei ist vor allem die minimal erreichbare Kollektor-Emitter-Spannung
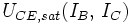 interessant. Aufgelöst für diese Spannung erhält man die Gleichung
interessant. Aufgelöst für diese Spannung erhält man die GleichungBei
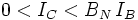 gilt
gilt  . Das Minimum erhält man bei IC = 0:
. Das Minimum erhält man bei IC = 0:Für den Inversbetrieb vertauscht man Emitter und Kollektor. Dadurch erhält man für die Sättigung mit IE = 0:
Da AI < AN < 1 gilt UEC,sat(IE = 0) < UCE,sat(IC = 0). Dabei gilt üblicherweise
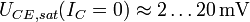 und
und 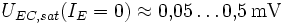 .
.Transportmodell
Durch die Umformung der beiden Stromquellen des Ebers-Moll-Modells in eine einzige gesteuerte Stromquelle erhält man das Transportmodell des Bipolartransistors. Das Transportmodell beschreibt das Gleichstromverhalten. Die Emitter und Kollektor-Diode wird dabei als ideal angenommen und der durch die Basis fließende Strom wird als Transportstrom IT getrennt berechnet. Für das Transportmodell gelten die folgenden Gleichungen:
Da für den Normalbetrieb die Sperrströme vernachlässigt werden können, erhält man das reduzierte Transportmodell mit:
Modellierung statischer Effekte im Transportmodell
Um das statische Verhalten des Bipolartransistors besser modellieren zu können, muss das Transportmodell entsprechend erweitert werden. Hierbei sind vor allem die folgenden Effekte zu berücksichtigen:
- Leckströme
- Hochstromeffekt
- Early-Effekt
Für das um diese Effekte erweiterte Transportmodell gelten im Allgemeinen die Zusammenhänge:
- IB = IB,N + IB,I + IB,E + IB,C


was sich aus den im Weiteren erläuterten Formeln ergibt.
Leckströme
Die Leckströme, die durch die Ladungsträgerrekombination in den pn-Übergängen erzeugt wird werden zu den jeweiligen Strömen der Kollektor- und der Emitter-Diode hinzuaddiert. Dies wird erreicht, indem man den Dioden im Transportmodell jeweils eine weitere Diode parallelschaltet. Diese zusätzlichen Dioden werden über die Leck-Sättigungs-Sperrströme IS,E und IS,C, sowie über die Emmissionskoeffizienten
 und
und 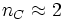 beschrieben.
beschrieben.Hochstrom- und Early-Effekt
Wenn der Strom durch den Transistor sehr stark ist, ist der Transportstrom eines realen Transistors durch die hohe Ladungsträgerkonzentration in der Basis kleiner als durch das Grundmodell dargestellt. Dieser Effekt wird auch als Hochstromeffekt bzw. als starke Injektion bezeichnet.
Zusätzlich beeinflussen die Spannungen UBE und UBC die effektive Dicke der Basiszone und wirken sich somit auf den Transportstrom IT aus. Dieser Effekt ist als Early-Effekt bekannt.
Der Hochstrom- und der Early-Effekt wird durch die dimensionslose Größe qB dargestellt.
qB ist hierbei die relative Majoritätsträgerladung und setzt sich aus der Größe des Early-Effekts qEarly und der Größe des Hochstromeffektes qHoch zusammen:
Hierbei sind UA,N und UA,I die Early-Spannungen mit
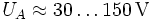 . IK,N und IK,I sind die Knieströme der starken Injektion. Die Größe der Knieströme ist von der Größe und damit der Bauform des Transistors abhängig und liegen im Milliampere- (Kleinleistungtransitor) bis Amperebereich (Leistungstransistor).
. IK,N und IK,I sind die Knieströme der starken Injektion. Die Größe der Knieströme ist von der Größe und damit der Bauform des Transistors abhängig und liegen im Milliampere- (Kleinleistungtransitor) bis Amperebereich (Leistungstransistor).Hochstrom- und Early-Effekt im Normalbetrieb
 Gummel-Plot mit UCE = konst.
Gummel-Plot mit UCE = konst.Bei der Betrachtung des Kollektorstromes kommt die Auswirkung des Faktors qB besonders zur Geltung. Unter Vernachlässigung der Sperrströme erhält man:
Bei kleinen bis mittleren Stromgrößen IC < IK,N gilt
 und somit
und somit  . Zusätzlich gilt
. Zusätzlich giltda
 . Somit erhält man eine Näherungsgleichung für den Early-Effekt:
. Somit erhält man eine Näherungsgleichung für den Early-Effekt:und durch Einsetzen in IC erhält man:
Bei großen Strömen
 ist
ist  und somit
und somit  . Durch Einetzen erhält man:
. Durch Einetzen erhält man:Unter Vernachlässigung der Sperrströme erhält man für IB die Gleichung
Stromverstärkung
Für die Stromverstärkung B gilt der Zusammenhang
Zudem ist die Stromverstärkung B von UBE und UCE abhängig, da auch IC und qB von diesen Spannungen abhängig sind.
Der Verlauf der Stromverstärkung wird zur Näherung in drei Abschnitte unterteilt:
-
- 1. Leckstrombereich
- Bei kleinen Kollektorströmen dominiert der Leckstromanteil IB,E im Basisstrom IB. Dieser Bereich wird folglich als Leckstrombereich bezeichnet. In diesem Bereich gilt aufgrund der Dominanz des Leckstromes die Näherung
 und
und  . Daraus ergibt sich die Vereinfachung:
. Daraus ergibt sich die Vereinfachung:
- Mit
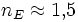 erhält man
erhält man  . Damit ist die Verstärkung B in diesem Bereich kleiner als bei mittelgroßen Kollektorströmen und wird mit steigendem Kollektorstrom IC ebenfalls größer.
. Damit ist die Verstärkung B in diesem Bereich kleiner als bei mittelgroßen Kollektorströmen und wird mit steigendem Kollektorstrom IC ebenfalls größer.
-
- 2. Normalbereich
- Bei mittleren Kollektorströmen gilt die Näherung
 und daraus folgend:
und daraus folgend:
- Daraus ergibt sich ein maximaler Wert, sowie nur eine geringe Abhängigkeit von IC, für die Verstärkung B in diesem Bereich. Deshalb werden Transistoren bevorzugt in diesem Bereich betrieben.
-
- 3. Hochstrombereich
- Bei großen Kollektorströmen kommt es zum Hochstromeffekt. Über den Zusammenhang
 erhält man den Zusammenhang:
erhält man den Zusammenhang:
- Die Stromverstärkung B ist somit indirekt proportional zu IC, was bedeutet, dass die Stromverstärkung mit steigendem Kollektorstrom stark abnimmt.
Die maximale Stromverstärkung bei konstanter Kollektor-Emitter-Spannung wird mit Bmax(UCE) bezeichnet. Für Transistoren mit großem Kniestrom IK,N und kleinem Leckstrom IS,E ist der Normalbereich so breit, dass der tatsächliche Verlauf von B mit der Näherungsgeraden in diesem Bereich eine Tangente bildet. Im Schnittpunkt gilt Bmax(UCE) = B0,max = BN, wobei B0,max bei UCE = 0 auftritt. Bei Transistoren mit kleinem Kniestrom und großem Leckstrom hingegen fällt der Normalbereich sehr schmal aus, wobei die Verstärkung unterhalb der Näherungsgeraden bleibt und damit B < BN gilt.
Bahnwiderstände
Da das Halbleitermaterial für den elektrischen Strom einen Widerstand darstellt, muss dieser Widerstand in Form der Bahnwiderstände dargestellt werden. Man unterscheidet zwischen dem Emitterbahnwiderstand RE, dem Kollektorbahnwiderstand RC und dem Basisbahnwiderstand RB.
- Emitterbahnwiderstand
- Aufgrund der starken Dotierung und des geringen Längen-zu-Querschnitt-Verhältnisses des Emitters hat RE nur einen kleinen Betrag. Bei Kleinleistungstransistoren beträgt RE etwa 0,1 Ω bis 1 Ω und bei Leistungstransistoren etwa 0,01 Ω bis 0,1 Ω.
- Kollektorbahnwiderstand
- Der Kollektorbahnwiderstand wird vor allem durch die schwach dotierte Kollektorzone verursacht. Bei Kleinleistungstransistoren beträgt RC etwa 1 Ω bis 10 Ω und bei Leistungstransistoren etwa 0,1 Ω bis 1 Ω.
- Basiswiderstand
- Der Baisiswiderstand wird aus dem externen Basiswiderstand RBe und dem internen Basiswiderstand RBi gebildet. Der externe Basiswiderstand tritt hierbei zwischen dem Kontakt der Basis und der aktiven Basiszone auf, während der interne Basiswiderstand quer in der aktiven Basiszone zwischen Emitter und Kollektor auftritt. Bei großen Strömen hat der interne Basiswiderstand nur begrenzt Einfluss, da sich der Strom aufgrund der Stromverdrängung an der Basiszone konzentriert. Zusätzlich wirkt der Early-Effekt, der die Dicke der Basiszone beeinflusst. Diese Effekte werden in der Konstante qB zusammengefasst.
- Der Basiswiderstand ergibt sich folglich aus:
- Für den Normalbetrieb folgt durch Auflösen von qB:
- Bei Kleinleistungstransistoren beträgt RBe etwa 10 Ω bis 100 Ω und bei Leistungstransistoren etwa 1 Ω bis 10 Ω. RBi ist hierbei etwa drei- bis viermal so groß wie RBe.
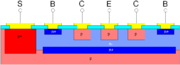
Substrat-Diode
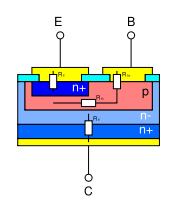
Bei integrierten Transistoren ist bei vertikalen npn-Transistoren zwischen Substrat und Kollektor, sowie bei lateralen pnp-Transistoren zwischen Substrat und Basis, konstruktionsbedingt—wie in den nebenstehenden Abbildungen dargestellt—ein pn-Übergang: die sog. Substrat-Diode. Diese Substrat-Diode wird als herkömmliche pn-Diode üder die Shockley-Formel beschrieben. Hierbei wird für den Sättigungssperrstrom IS der Sättigungssperrstrom der Substratdiode IS,S eingesetzt:
 (lateral)
(lateral) (vertikal)
(vertikal)
Da die Substrat-Diode üblicherweise nicht beschalten wird, ist keine Modellierung erforderlich. Bei (fehlerhafter) Beschaltung kann jedoch ein Strom fließen und muss in diesem Fall auch berücksichtigt werden.
Modellierung dynamischer Effekte im Transportmodell
Bei der Ansteuerung mit sinus- oder pulsförmigen Signalen muss auch das dynamische Verhalten des Transistors beachtet werden. Hierzu benötigt man, wie bei der Diode, die im Transistor auftretenden Sperr- und Diffusionskapazitäten.
Sperrschichtkapazitäten
Bei einem einzelnen Bipolartransistor treten zwei und bei integrierten Transistoren drei Sperrschichtkapazitäten auf. Die Emitterdiode ist hierbei durch die Emittersperrschichtkapazität
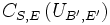 charakterisiert. Die Kollektordiode wird durch die Kollektorsperrschichtkapazität CC,E beschrieben, welche sich aus der internen Sperrschichtkapazität CS,Ci der aktiven Zone bei B' und der externen Sperrschichtkapazität CS,Ce beim Basisanschluss B zusammen. Die Anteile der internen und externen Sperrschichtkapazität an der Kollektorsperrschichtkapazität wird durch den Parameter xCSC dargestellt:
charakterisiert. Die Kollektordiode wird durch die Kollektorsperrschichtkapazität CC,E beschrieben, welche sich aus der internen Sperrschichtkapazität CS,Ci der aktiven Zone bei B' und der externen Sperrschichtkapazität CS,Ce beim Basisanschluss B zusammen. Die Anteile der internen und externen Sperrschichtkapazität an der Kollektorsperrschichtkapazität wird durch den Parameter xCSC dargestellt:Bei Einzeltransistoren liegt der Faktor xCSC meistens zwischen 0,5 und 1, was bedeutet, dass
 ist. Bei integrierten Transistoren ist xCSC < 0,5 und damit CS,Ce > CS,Ci.
ist. Bei integrierten Transistoren ist xCSC < 0,5 und damit CS,Ce > CS,Ci.Bei integrierten Transistoren tritt zusätzlich die Sperrschichtkapazität der Substratdiode CS,S auf. Diese wirkt bei integrierten vertikalen npn-Transistoren am internen Kollektor C' und bei integrierten lateralen npn-Transistoren an der internen Basis B'. Daher gilt:
Diffusionskapazitäten
Beim Transistor treten zwei Diffusionskapazitäten auf: die Diffusionskapazität der Emitterdiode CD,N und die Diffusionskapazität der Kollektordiode CD,I. In diesen werden die Emitterdiffusionsladung QD,N und die Kollektordiffusionsladung QD,I gespeichert. Die Diffusionsladungen ergeben sich aus dem Transportstrom IT, welcher vom Kollektor zum Emitter fließt (siehe auch: Transportmodell).
Wobei die Zeitkonstanten τN und τI als Transit-Zeit bezeichnet werden. Durch Differentiation ergeben sich aus diesen Gleichungen die Diffusionskapazitäten:
Die Diffusionskapazitäten CD,N und CD,I treten parallel zu den Sperrschichtkapazitäten CS,E und CS,Ci auf. Im Normalbetrieb ist die Kollektor-Diffusionskapazität CD,I aufgrund der geringen inneren Basis-Kollektor-Spannung UB',C' im Vergleich zur inneren Kollektor-Sperrschicht-Kapazität CS,Ci sehr klein und kann daher vernachlässigt werden. CD,I kann infolge der Vernachlässigung von CD,I mit einer konstanten Transitzeit beschrieben werden, wodurch τN = τ0,I angenommen wird.
Wenn der Transitstrom klein ist gilt CD,N < CD,N, bei großem Transitstrom hingegen gilt CD,N > CD,N. Um dies korrekt darstellen zu können muss τN in der Ersatzschaltung genau modelliert werden. Eine Zunahme von τN gei großen Strömen wirkt sich als Abnahme der Grenzfrequenzen und der Schaltgeschwindigkeit des Transistors aus.
Aufgrund des Hochstromeffektes nimmt die Diffusionsladung überproportional zu. Die Transitzeit ist daher nicht konstant und nimmt mit steigendem Strom zu. Der Early-Effekt wirkt sich ebenfalls aus, da dieser die effektive Dicke der der Basiszone und damit die in der Basiszone gespeicherte Ladung verändert. Da jedoch mit den Parametern IK,N und UA,N keine präzise Beschreibung möglich ist, wird eine empirisch bestimmte Gleichung zur Beschreibung verwendet:
wobei der Faktor x für das Polynom über die folgende Gleichung definiert ist:
Zusätzlich ist τ0,N die ideale Transitzeit,
 der Koeffizient der Transitzeit, IK,N der Transitzeit-Kniestrom und Uτ,N die Transitzeit-Spannung. Der Koeffizient der Transitzeit
der Koeffizient der Transitzeit, IK,N der Transitzeit-Kniestrom und Uτ,N die Transitzeit-Spannung. Der Koeffizient der Transitzeit  gibt hierbei an, wie stark τN bei
gibt hierbei an, wie stark τN bei  zunehmen kann:
zunehmen kann:Die Hälfte der maximalen Zunahme erhält man bei
 :
:Daraus folgt, dass wenn die Spannung UB'C' um den Betrag der Spannung Uτ,N sinkt, steigt τN nur noch mit der halben Geschwindigkeit. d. h. für
 ist die Zunahme von τN um den Faktor 2n kleiner.
ist die Zunahme von τN um den Faktor 2n kleiner.Statisches Kleinsignalmodell
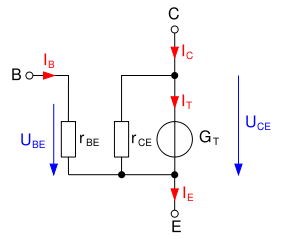
Das statische Kleinsignalmodell beschreibt das Kleinsignalverhalten bei niedrigen Frequenzen und wird deshalb auch als Gleichstrom-Kleinsignalersatzschaltbild bezeichnet.
Aus dem Gummel-Poon-Modell wird durch Linearisierung im Arbeitspunkt das lineare Kleinsignalmodell. Der Arbeitspunkt wird hierbei in einem Bereich gewählt, in dem der Transistor nach erfolger Dimensionierung arbeiten soll. Üblicherweise ist dies der Normalbetrieb, weshalb im Weiteren Modelle für den Normalbetrieb gezeigt werden. Nach denselben Prinzipien kann man jedoch auch Modelle für die anderen Transistor-Betriebsarten erstellen.
Die Linearisierung des Gummel-Poon-Modells erfolgt, indem man die Kapazitäten weglässt – da diese bei Gleichstrom nicht wirken – und die Sperrströme vernachlässigt – also IB,I, IB,C und ID,S gleich Null setzt.
Weiters werden die nichtlinearen Größen
 sowie
sowie 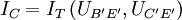 im Arbeitspunkt A linearisiert:
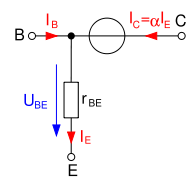
im Arbeitspunkt A linearisiert:In der Praxis werden zur weiteren Vereinfachung auch die Bahnwiderstände nicht berücksichtigt. Daraus erhält man das vereinfachte statische Kleinsignalmodell. Bei einer zusätzlichen Vernachlässigung des Early-Effektes durch
 erhält man des Weiteren eine alternative Darstellungsart dieses vereinfachten Modells, welche durch Linearisierung aus dem vereinfachten statischen Kleinsignalmodell erstellt wird. Die alternative Darstellungsart ist aufgrund des vernachlässigten Early-Effekts jedoch nur Ausnahmefällen brauchbar, da die Berechnung anhand dieser Vereinfachung meist zu unbrauchbaren Ergebnissen führt. In der Literatur findet man zudem oft eine Darstellung mit einem zusätzlichen Widerstand zwischen Basis und Kollektor, der sich durch die Linearisierung der Kollektor-Basis-Diode aus dem Ebers-Moll-Modell ergibt, jedoch nicht zur Modellierung des Early-Effekts dient.
erhält man des Weiteren eine alternative Darstellungsart dieses vereinfachten Modells, welche durch Linearisierung aus dem vereinfachten statischen Kleinsignalmodell erstellt wird. Die alternative Darstellungsart ist aufgrund des vernachlässigten Early-Effekts jedoch nur Ausnahmefällen brauchbar, da die Berechnung anhand dieser Vereinfachung meist zu unbrauchbaren Ergebnissen führt. In der Literatur findet man zudem oft eine Darstellung mit einem zusätzlichen Widerstand zwischen Basis und Kollektor, der sich durch die Linearisierung der Kollektor-Basis-Diode aus dem Ebers-Moll-Modell ergibt, jedoch nicht zur Modellierung des Early-Effekts dient.Hierbei gelten die Gleichungen
Modelle für das dynamische Verhalten
Gummel-Poon-Modell
Das Gummel-Poon-Modell, benannt nach seinen geistigen Vätern Hermann Gummel und H. C. Poon, ist das vollständige Modell eines Bipolar-Transistors und wird zur Schaltungssimulation – etwa in PSpice – verwendet. Es basiert auf dem Transportmodell und modelliert alle statischen und dynamischen Effekte in diesem.
Falls einige Werte im Datenblatt des Transistors nicht angegeben sind, werden (z. B. in PSpice) Standardwerte verwendet. In PSpice werden hierbei die folgenden Standardwerte verwendet:
Standardwerte des Gummel-Poon-Modell in PSpice Parameter IS BN BI nE nC xT,I fS Udiff,E, Udiff,C, Udiff,S mS,E, mS,C xCSC IS,S, IS,E, IS,C,
RB, RC, RE,
CS0,E, CS0,C, CS0,S,
τ0,N, τ0,I, xτ,N, xT,B,
mS,S, Iτ,NIK,N, IK,I,
UA,N, UA,I, Uτ,NStandardwert 10-16 A 100 1 1,5 2 3 0,5 0,75 V 333·10-3 1 0 ∞ Hierbei bedeutet ein Standardwert von 0 oder ∞, dass der entsprechende Parameter so gesetzt wird, dass dieser Parameter keinen Einfluss auf die Berechnung hat und auf diese Weise nicht modelliert wird.
Werte für das Gummel-Poon-Modell ausgewählter Einzeltransistoren Parameter PSpice-
BezeichnungBC547B [1] BC557B [2] BUV47 [3] BFR92P [4] IS IS 7 fA 1 fA 974 fA 0,12 fA BN BF 375 307 95 95 BI BR 13) 6,5 20,9 10,7 IS,E ISE 68 fA 10,7 fA 2,57 pA 130 fA nE NE 1,58 1,76 1,2 1,9 IK,N IKF 82 mA 92 mA 15,7 A 160 mA UA,N VAF 63 V 52 V 100 V 30 V RBe RBM 10 Ω1) 10 Ω1) 100 mΩ1) 6,2 Ω RBi2) — 01) 01) 01) 7,8 Ω — RB2) 10 Ω1) 10 Ω1) 100 mΩ1) 15 Ω RC RC 1 Ω 1,1 Ω 35 mΩ 140 mΩ CS0,E CJE 11,5 pF 30 pF 1,093 nF 1 fF Udiff,E VJE 500 mV 500 mV 500 mV 710 mV mS,E MJE 672·10-3 333·10-3 3) 333·10-3 3) 347·10-3 CS0,C CJC 5,25 pF 9,8 pF 364 pF 649 fF Udiff,C VJC 570 mV 490 mV 500 mV 850 mV mS,C MJC 315·10-3 332·10-3 333·10-3 3) 401·10-3 xCSC XCJC 13) 13) 13) 130·10-3 fS FC 500·10-3 3) 500·10-3 3) 500·10-3 3) 500·10-3 3) τ0,N TF 410 ps 612 ps 51,5 ns 27 ps xτ,N XTF 40 26 205 380·10-3 Uτ,N VTF 10 V 10 V 10 V 330 mV Iτ,N ITF 1,49 A 1,37 A 100 A 4 mA τ0,I TR 10 ns 10 ns 988 ns 1,27 ns xT,I XTI 33) 33) 33) 33) xT,B XTB 1,5 1,5 1,5 1,5 1) Wert nur allgemein angegeben. Bei hohen Frequenzen kommt es zu Ungenauigkeiten.
Dies wird im Transistorrauschen berücksichtigt. Andernfalls müsste der korrekte Wert durch Messung am einzelnen Bauteil ermittelt werden.
2) RBi wird in PSpice nicht explizit angegeben. Stattdessen wird RB mit RB = RBM + RBi = RBe + RBi angegeben.
3) entspricht dem StandardwertZudem werden in PSpice einige weitere Effekte berücksichtigt, die im PSpice Referenzhandbuch [5] beschrieben werden, wofür das in PSpice verwendete Modell entssprechend erweitert wurde.
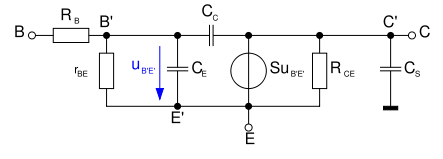
Dynamisches Kleinsignalmodell
Wenn man das vollständige statische Kleinsignalmodell um die Sperrschicht- und Diffuionskapazitäten erweitert erhält man das dynamische Kleinsignalmodell.
Die Emitterkapazität CE setzt sich aus der Emitter-Sperrschicht-Kapazität CS,E und der Diffusionskapazität für den Normalbetrieb CD,N zusammen:
Die interne Kollektorkapazität CCi entspricht der internen Kollekor-Sperrschicht-Kapazität, da die interne Diffusionskapazität CD,I wegen
 vernachlässigbar klein ist:
vernachlässigbar klein ist:Die externe Kollektorkapazität CCe und die Substratkapazität CS entsprechen den jeweiligen Sperrschichtkapazitäten, wobei die Substratkapazität naturgemäß nur bei integrierten Transistoren zu finden ist:
In der Praxis werden der Emitterwiderstand RE und der Kollektorwiderstand RC meist vernachlässigt, während der Basiswiderstand RB nur in Ausnahmefällen vernachlässigt werden kann, da der Basiswiderstand einen starken Einfluss auf das dynamische Verhalten hat. Zudem wird in der Praxis die interne und externe Kollektorkapazität – ausgenommen bei integrierten Transistoren mit einer überwiegend externen Kollektorkapazität – als interne Kollektorkapazität CC zusammengefasst. Hieraus erhält man das vereinfachte dynamische Kleinsignalmodell:
Grenzfrequenz im Kleinsignalbetrieb
Mit Hilfe des Kleinsignalmodells kann man die Frequenzgänge der Kleinsignalstromvertärkungen α und β, sowie der Transmittanz
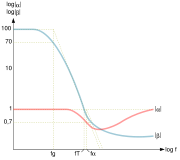
 , rechnerisch ermitteln. Die jeweiligen Grenzfrequenzen fα, fβ, fY21e, sowie die Transitfrequenz fT stellen ein Maß für die Schaltgeschwindigkeit und Bandbreite des Transistors dar. Hierbei gilt der Zusammenhang
, rechnerisch ermitteln. Die jeweiligen Grenzfrequenzen fα, fβ, fY21e, sowie die Transitfrequenz fT stellen ein Maß für die Schaltgeschwindigkeit und Bandbreite des Transistors dar. Hierbei gilt der Zusammenhang
Wird der Transistor in Emitterschaltung mit einer Stromquelle – bzw. mit einer Quelle mit einem Innenwiderstand Ri von –betrieben, spricht man von einer Stromsteuerung. Die Grenzfrequenz wird in diesem Fall durch die β-Grenzfrequenz fβ nach oben begrenzt.
–betrieben, spricht man von einer Stromsteuerung. Die Grenzfrequenz wird in diesem Fall durch die β-Grenzfrequenz fβ nach oben begrenzt.Wird der Transistor hingegen in Emitterschaltung mit einer Spannungsquelle – bzw. mit einer Quelle mit einem Innenwiderstand Ri von
 –betrieben, spricht man von Spannungssteuerung. Die Grenzfrequenz wird in diesem Fall durch die Steilheitsgrenzfrequenz fY21e nach oben begrenzt.
–betrieben, spricht man von Spannungssteuerung. Die Grenzfrequenz wird in diesem Fall durch die Steilheitsgrenzfrequenz fY21e nach oben begrenzt.Daraus folgt, dass man bei Spannungssteuerung eine höhere Grenzfrequenz und damit Bandbreite erreichen kann. Dies gilt auch für die Kollektorschaltung. Die größte Bandbreite erreicht jedoch die Basisschaltung bei der allgemein die Bedingung Ri > rE gilt und damit eine Stromsteuerung vorliegt und die Bandbreite durch die α-Grenzfrequenz fα nach oben begrenzt wird.
Die Bandbreite der Schaltung ist zusätzlich vom Arbeitspunkt abhängig. In Emitterschaltung mit Stromsteuerung und bei der Basisschaltung erhält man die maximale Bandbreite, indem man den Kollektorstrom IC,A so einstellt, dass die Transitfrequenz den maximalen Wert erreicht. Bei der Emitterschaltung mit Spannungssteuerung besteht ein komplizierterer Zusammenhang, da zwar die Steilheitsfrequenz fY21e mit steigendem Kollektorstrom IC,A abnimmt, aber gleichzeitig die Schaltung der Kollektorschaltung niederohmiger wird und dadurch die ausgangsseitige Bandbreite der Schaltung erhöht wird.Die Transitfrequenz fT und die Ausgangskapazität in Basisschaltung Cobo (output, grounded base, open emitter) wird im Datenblatt des Transistors angegeben. Hierbei entspricht Cobo der Kollektor-Basis-Kapazität CCB. Hieraus ergibt sich:
Literatur
- Ulrich Tietze, Christoph Schenk, Eberhard Gamm: Halbleiter-Schaltungstechnik. 12. Auflage, Springer 2002. ISBN 3540428496
- Paul R. Gray, Paul J. Hurst, Stephen H. Lewis, Robert G. Meyer: Analysis and Design of Analog Integrated Circuits. Wiley 2001. ISBN 0471321680
- Simon M. Sze: Physics of Semiconductor Devices. Wiley 1981. ISBN 0471056618
- Hans-Martin Rein, Roland Ranfft: Integrierte Bipolarschaltungen. Springer 1980, ISBN 3540096078
- Giuseppe Massobrio, Paolo Antognetti: Semicondurctor Device Modelling with SPICE. McGraw-Hill Professional 1998. ISBN 0071349553
Fußnoten und Einzelnachweise
Wikimedia Foundation.










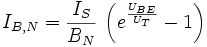


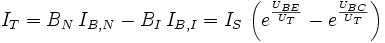
![I_C = I_S \, \left[ e^\frac{U_{BE}}{U_T} - \left( 1 + \frac{1}{B_I} \right) \, e^\frac{U_{BC}}{U_T} + \frac{1}{B_I} \right]](/pictures/dewiki/51/3d467b1159f5acfb0ff1d98b772f13d0.png)
![I_E = I_S \, \left[ e^\frac{U_{BC}}{U_T} - \left( 1 + \frac{1}{B_I} \right) \, e^\frac{U_{BE}}{U_T} + \frac{1}{B_N} \right]](/pictures/dewiki/100/d5551bbdefc97109b996762752c8160d.png)
_svg.png)
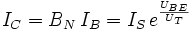








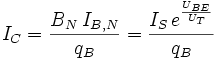




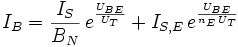




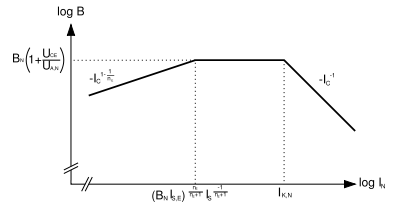











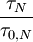 in doppellogarithmischer Darstellung
in doppellogarithmischer Darstellung![\tau_N = \tau_{0,N} \, \left[ 1 + x_{\tau,N} \, \left( 3\,x^2 - 2\,x^3 \right) \, 2^\frac{U_{B'C'}}{U_{\tau,N}} \right]](/pictures/dewiki/53/5e7b8057054124b8d119ca7771d80879.png)
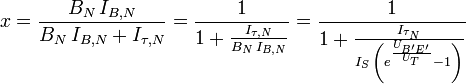
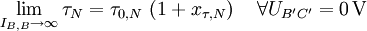

_svg.png)
_svg.png)
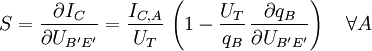
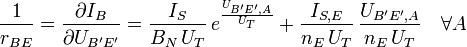


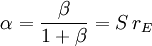


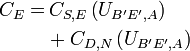


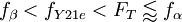
 und
und