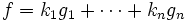Gröbner-Basis

Eine Gröbnerbasis (nach Bruno Buchberger, 1965) bzw. Standardbasis (nach Heisuke Hironaka, 1964) ist eine endliche Idealbasis zu einem Ideal I im Polynomring $K[X_1,\ldots,X_n]$ über dem (kommutativen) Körper K, die besonders gut dafür geeignet ist, zu entscheiden, ob ein gegebenes Polynom zum Ideal gehört oder nicht.

Hat man ein Polynom f und eine endliche Idealbasis 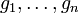$g_1,\ldots,g_n$ (diese existiert nach dem Hilbertschen Basissatz immer), so gehört f genau dann zu dem von 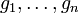$g_1,\ldots,g_n$ erzeugten Ideal, wenn sich f als Linearkombination

$f = k_1g_1+\cdots+k_ng_n$

der g_i mit polynomialen Koeffizienten 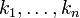$k_1,\ldots,k_n$ schreiben lässt. Um dies zu überprüfen, könnte man ähnlich wie im univariaten Fall versuchen, f um Vielfache der g_i mittels Division mit Rest zu reduzieren. Der praktischen Ausführung stehen zwei Probleme gegenüber.

1. Zum einen ist, konträr zum univariaten Fall, auf den Monomen multivariater Polynome keine natürliche Ordnung definiert.
2. Zum zweiten kann man je nach Wahl der Reihenfolge der in der Reduktion verwandten g_i verschiedene nicht weiter reduzierbare Reste erhalten.

Um das erste Problem zu beheben, ordnet man die Monome mittels einer zulässigen Monomordnung bzw. Termordnung „ < “ an. Man definiert eine Halbordnung der Polynome durch Vergleich der in der Monomordnung jeweils führenden Monome.

Gibt es nun ein g_i, so dass das Leitmonom (das bezüglich der Monomordnung größte Monom) Lm(g_i) = g_i,bX^b von g_i ein beliebiges Monom f_aX^a von 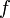$f\;$ teilt (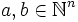$a,b\in\N^n$ sind Multiindizes), so gilt 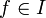$f \in I$ genau dann, wenn 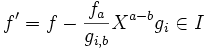$f' = f - \frac{f_a}{g_{i,b}}X^{a-b}g_i \in I$ gilt. f' wird Reduktion von f genannt.

Wurde nach dem führenden Monom Lm(f) = f_aX^a von f reduziert, so gilt 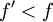$f\!\,' &amp;lt; f$. Man hat also das Problem auf eine kleinere Instanz desselben Typs reduziert. Erreicht man nach einer endlichen Anzahl von Reduktionsschritten f' = 0, so gilt offensichtlich 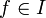$f \in I$. Jedoch kann ebenso der Fall eintreten, dass man nach einer endlichen Anzahl von Schritten auf ein nicht weiter reduzierbares Polynom stößt, welches von Null verschieden ist. Man kann daraus aber im Allgemeinen nicht folgern, dass 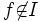$f \not\in I$ gilt.

Definition: 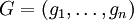$G=(g_1,\ldots,g_n)$ ist eine Gröbnerbasis (bezüglich < ) von I, falls diese Schlussfolgerung für alle f korrekt ist, wenn es also für alle 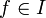$f \in I$ ein g_i gibt, so dass das Leitmonom von g_i das von f teilt. Anders gesagt, jedes Element aus I wird, in jeder Reihenfolge der Reduktionsschritte, auf das Nullpolynom reduziert.

Gröbnerbasen können mit dem Buchberger-Algorithmus berechnet werden. Dabei werden Vervollständigungs-Techniken benutzt, wie sie auch beim Theorembeweisen eingesetzt werden.

Literatur

• Heisuke Hironaka: Resolution of singularities of an algebraic variety over a field of characteristic zero, In: Annals of Mathematics 79 (1964), Nr. 1, S. 109–326
• Bruno Buchberger: Ein Algorithmus zum Auffinden der Basiselemente des Restklassenringes nach einem nulldimensionalen Polynomideal. Österreich, Universität Innsbruck, Diss., 1965
• Bruno Buchberger:Ein algorithmisches Kriterium für die Lösbarkeit eines algebraischen Gleichungssystems. Aequationes Mathematicae 4 (1970): 374-383.
• T. Becker, B. V. Weispfenning: Gröbner bases: a computational approach to commutative algebra. Graduate Texts in Mathematics: readings in mathematics. Bd. 141, New York: Springer Verlag, 1993
• David Cox; Little, John; O'Shea, Donald: Ideals, varieties, and algorithms. New York: Springer-Verlag, 1997
• Joachim von z. Gathen, Jürgen Gerhard: Modern Computer Algebra. Cambridge University Press, 1999