- Größte Paarung
-
Eine Paarung (Matching) ist in der Graphentheorie eine Teilmenge der Kanten eines Graphen, in der keine zwei Kanten einen gemeinsamen Knoten besitzen. Paarungen haben innerhalb der Graphentheorie einen weiten Anwendungsbereich.
Inhaltsverzeichnis
Definitionen
Sei G=(V,E) ein ungerichteter Graph ohne Mehrfachkanten und M eine Teilmenge von E. Man bezeichnet M als Paarung, Matching, Zuordnung oder unabhängige Kantenmenge von G, wenn je zwei beliebige verschiedene Kanten e1 und e2 disjunkt sind, d.h. mit verschiedenen Knoten inzident sind. Ist ein Knoten von G in einer Kante einer Paarung enthalten, so nennt man ihn von der Paarung überdeckt. Alternativ werden auch die Begriffe saturiert und gepaart verwendet.
Eine Paarung M von G nennt man maximal oder nicht erweiterbar, wenn man keine weitere Kante e aus E zu M hinzufügen kann, so dass M zusammen mit e eine Paarung ist. Gibt es in G keine Paarung, die mehr Elemente als M enthält, so nennt man M größte Paarung oder Maximum-Matching. Ist jeder Knoten von V Element einer Kante von M (also von M überdeckt), so nennt man M eine perfekte Paarung. Die Anzahl der Elemente einer größten Paarung nennt man Paarungszahl bzw. Matchingzahl.
Einen k-regulären Teilgraphen von G (das ist ein Teilgraph, dessen sämtliche Knoten sowohl den Eingangs- wie auch den Ausgangsgrad k haben) nennt man einen k-Faktor, wenn er alle Knoten von G enthält. Die Kantenmenge eines 1-Faktors ist also offensichtlich eine perfekte Paarung.
In kantengewichteten Graphen definiert man die Größe einer Paarung über die Summe ihrer Kantengewichte. Als größte gewichtete Paarung eines Graphen G bezeichnet man dann eine Paarung, die diesen Wert maximiert.
In gerichteten Graphen und solchen mit Mehrfachkanten werden Paarungen nicht betrachtet. Ersteres, weil es bei Paarungen nicht auf die Richtung der Kanten ankommt, Letzteres, weil von den Mehrfachkanten nur eine für eine Paarung in Frage kommt. Es spielt also keine Rolle, ob man den Graphen betrachtet, der entsteht, wenn man die Vielfachheiten von Mehrfachkanten auf 1 reduziert oder ob man den Originalgraph mit Mehrfachkanten betrachtet.
Die nachfolgenden Definitionen dienen dem Verständnis der unten gegebenen Aussagen und Sätze.
Ein alternierender Pfad bezüglich einer Paarung ist ein Pfad, dessen Kanten abwechselnd zur Paarung und nicht zur Paarung gehören. Auf eine Kante der Paarung folgt also immer eine Kante, die nicht zur Paarung gehört und umgekehrt. Manche Autoren setzen zusätzlich voraus, dass ein alternierender Pfad mit einem Knoten beginnt, der von der Paarung nicht überdeckt wird. Beginnt und endet ein alternierender Pfad in unterschiedlichen Knoten, die von der Paarung nicht überdeckt werden, so spricht man von einem augmentierenden Pfad oder Verbesserungspfad.
Bezeichnet q(G) die Anzahl der Zusammenhangskomponenten mit ungerader Anzahl Knoten in einem Graphen G=(V,E), so nennt man def(G):=q(G-S)-|S| für ein Teilmenge S von V Defekt von G, falls q(G-U)-|U|≥q(G-S)-|S| für jede andere Teilmenge U von V gilt. G-S bzw. G-U bezeichnet dabei den Graphen, der entsteht, wenn man die Knoten von S bzw. U und ihre inzidenten Kanten aus G löscht.
Beispiel
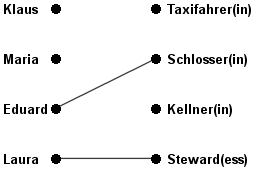
Dem Arbeitsamt liegen vier Stellenangebote und ebenso viele Stellengesuche vor. Dabei haben einige Arbeitssuchende mehrere Berufe angegeben, für die sie qualifiziert sind. Zur Veranschaulichung der Ausgangssituation kann ein bipartiter Graph gezeichnet werden (Abb. 1): dabei steht jeder Knoten in der linken Teilmenge für einen Arbeitssuchenden und jeder in der rechten für eine offene Stelle. Ist ein Arbeitssuchender mit einem Stellenangebot mittels einer Kante verbunden, so bedeutet das, dass er für den entsprechenden Beruf qualifiziert ist. So ist z. B. Laura in der Lage, als Kellnerin oder Stewardess zu arbeiten; Eduard und Klaus sind beide gelernte Schlosser und konkurrieren um die offene Stelle.
Die Vermittlung von möglichst vielen Jobs ist ein Paarungs-Problem. Erneut werden die Stellengesuche und -angebote als Knoten eines bipartiten Graphen aufgefasst, diesmal stehen die Kanten jedoch für zugewiesene Jobs. Es sollen nun möglichst viele Kanten aus Abb. 1 übernommen werden, dabei darf an jedem Knoten allerdings höchstens eine Kante anliegen, denn natürlich kann für jedes Stellenangebot nur ein Bewerber angenommen werden, und jeder kann nur einen Job ausführen.
Kann der Mitarbeiter des Arbeitsamtes nicht alle Stellengesuche und -angebote bearbeiten, weil ihm nicht genug Zeit zur Verfügung steht, so vermittelt er unter Umständen weniger Jobs, als möglich wären. Im Beispiel (Abb. 2) wurden nur zwei Jobs vermittelt, und zwar soll Eduard Schlosser werden und Laura Stewardess. Man spricht dennoch von einer Paarung (Matching), denn niemandem wurden zwei Jobs vermittelt, und keine Arbeitsstelle wurde zwei Bewerbern zugewiesen.
Doch auch wenn das Arbeitsamt alle Möglichkeiten berücksichtigt, ist es in diesem Fall nicht möglich, allen Arbeitssuchenden einen Job zu vermitteln. Die größte Paarung ist also in diesem Fall keine perfekte Paarung. Die Gründe dafür sind, dass die beiden gelernten Schlosser um eine einzige Stelle konkurrieren, während Maria entweder Taxifahrerin oder Kellnerin wird und somit eine Stelle offen bleibt. Dass eine perfekte Paarung nicht möglich ist, lässt sich mit dem Heiratssatz von Hall (siehe unten) beweisen.
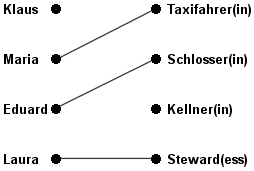
Das Arbeitsamt kann sich nun etwa entscheiden, Eduard die Stelle als Schlosser und Maria die als Taxifahrerin zu vermitteln (Abb. 3). Hier sieht man, dass es in einem Graphen mehr als eine größte Paarung geben kann: eine andere größte Paarung würde z. B. so aussehen, dass Klaus den Schlosserjob bekommt.
Nun kontaktiert das Arbeitsamt Klaus und berichtet ihm von dem Problem. Um nicht arbeitslos zu werden, erklärt dieser sich bereit, statt als Schlosser als Taxifahrer zu arbeiten. Dadurch ist es möglich, jedem Arbeitssuchenden eine Stelle zu vermitteln (Abb. 4). Graphentheoretisch betrachtet, inzidiert also jeder Knoten mit genau einer Kante. Man spricht von einer perfekten Paarung. Eine perfekte Paarung ist nur dann möglich, wenn genauso viele Stellengesuche wie -angebote vorliegen, und, wie wir gesehen haben, selbst dann nicht immer.
Wichtige Aussagen und Sätze
Eine maximale Paarung eines Graphen G enthält höchstens so viele Kanten wie eine größte Paarung in G (jede größte Paarung ist auch eine maximale Paarung). Andererseits enthält eine größte Paarung in G höchstens doppelt so viele Kanten wie eine maximale Paarung.
Von Claude Berge (1957) stammt ein leicht beweisbarer Satz, der besagt, dass eine Paarung M eines Graphen G genau dann eine größte Paarung von G ist, wenn es keinen augmentierenden Pfad zu M gibt. Mit Hilfe dieses Satzes lässt sich ein einfacher polynomieller Algorithmus entwerfen, der zu einem gegebenen Graphen ein größtes Matching findet, indem er nach augmentierenden Pfaden in einem Graphen sucht.
Man zeigt leicht, dass die Knotenüberdeckungszahl eines Graphen mindestens so groß ist, wie seine Paarungszahl, aber höchstens so groß wie das 2-fache seiner Paarungszahl. Für bipartite Graphen konnte König (1931) zeigen, dass die Paarungszahl genau der Knotenüberdeckungszahl entspricht (dies ist der sog. Satz von König). Dies impliziert insbesondere polynomielle Algorithmen zur Bestimmung der Knotenüberdeckungszahl und in Folge auch der Stabilitätszahl eines bipartiten Graphen. Im allgemeinen sind diese Probleme NP-schwer.
In Graphen mit ungerader Knotenzahl gibt es offensichtlich keine perfekten Paarungen, da jede Paarung eine gerade Anzahl Knoten überdeckt. Die Defektformel von Berge (1958) besagt jedoch, dass das 2-fache der Paarungszahl eines Graphen G der Anzahl Knoten von G abzüglich seines Defektes entspricht. Daraus leitet sich ein Satz von Tutte (1947) ab, der besagt, dass ein Graph G=(V,E) genau dann eine perfekte Paarung besitzt, wenn für jede Teilmenge S von V gilt: q(G-S)≤|S|. Ebenfalls folgt direkt der schon 1891 von Petersen damals sehr aufwändig bewiesene Satz, dass ein kubischer Graph mit höchstens zwei trennenden Kanten ein perfektes Matching besitzt.
In Graphen mit sehr vielen Kanten (sog. dichte Graphen) gibt es meistens auch eine (fast) perfekte Paarung. Algorithmisch interessant ist der Spezialfall, dass der Graph viele (fast) perfekte Paarungen besitzt und das Rechenverfahren die Aufgabe hat, eine solche Paarung zu finden.
weitere Algorithmen in Stichworten:- Ungarische Methode, Algorithmus von Hopcroft und Karp
- Auktionsalgorithmus nach Bertsekas (besonders für Graphen mit wenigen Kanten)
Paarungen in bipartiten Graphen
Eine wichtige Klasse von Graphen bilden im Zusammenhang mit Paarungen die bipartiten Graphen. Für sie sind eine Reihe spezieller Sätze und Algorithmen bekannt.
In bipartiten Graphen lässt sich mit dem Algorithmus von Hopcroft und Karp in
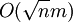 eine größte Paarung finden. Der Algorithmus basiert auf der Idee, simultan mehrere Verbesserungspfade zu finden.
eine größte Paarung finden. Der Algorithmus basiert auf der Idee, simultan mehrere Verbesserungspfade zu finden.Der so genannte Heiratssatz von Hall (1935) besagt, dass in bipartiten Graphen G mit Bipartition {A,B} genau dann eine Paarung existiert, die jeden Knoten aus A überdeckt, falls für jede Teilmenge S von A gilt, dass ihre Nachbarschaft mindestens so groß ist wie S selbst. Der Name Heiratssatz rührt daher, dass es nach diesem Satz möglich ist, jede Frau zu verheiraten, falls es für jede Gruppe von Frauen mindestens ebensoviele Männer gibt, die sich für wenigstens eine der Frauen in der Gruppe interessieren.
Der Satz von Hall hat einige direkt ableitbare Konsequenzen. Da in regulären bipartiten Graphen gilt, dass | A | = | B | , folgt auch dass auch die Heiratsbedingung
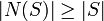 für jede Teilmenge S von A oder B immer erfüllt ist, so dass jeder bipartite reguläre Graph eine perfekte Paarung besitzt. Diesen Satz konnte König schon 1916 beweisen (damals natürlich unabhängig vom Heiratssatz). Mit Induktion über k folgt dann auch, dass ein k-regulärer Graph k disjunkte Paarungen besitzt, die zusammengenommen seine Kantenmenge ergeben. Hier wird der Sinn der Definition eines k-Faktors deutlich.
für jede Teilmenge S von A oder B immer erfüllt ist, so dass jeder bipartite reguläre Graph eine perfekte Paarung besitzt. Diesen Satz konnte König schon 1916 beweisen (damals natürlich unabhängig vom Heiratssatz). Mit Induktion über k folgt dann auch, dass ein k-regulärer Graph k disjunkte Paarungen besitzt, die zusammengenommen seine Kantenmenge ergeben. Hier wird der Sinn der Definition eines k-Faktors deutlich.Zusammenhang zwischen maximaler Paarung und maximalem Fluss
Man kann eine maximale Paarung berechnen indem man den bipartiten Graphen erweitert und im erweiterten Graphen einen maximalen Fluss berechnet. Für diese Aufgabe stehen mehrere Algorithmen zur Verfügung, die im Artikel Flüsse und Schnitte in Netzwerken aufgeführt sind.
Der erweiterte Graph geht aus dem bipartiten Graphen
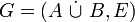 durch die folgenden Schritte hervor.
durch die folgenden Schritte hervor.- Hinzufügen einer Quelle s mit Kanten (s,a) zu jedem Knoten von A und einer Senke t mit Kanten (b,t) von jedem Knoten aus B.
- Die Kapazität jeder Kante des Netzwerks ist 1.
- Die ungerichteten Kanten werden durch gerichtete in Richtung der Senke ersetzt.
Das folgende Beispiel zeigt den bipartiten Graphen und den zugehörigen erweiterten Graphen.
Auf dem so definierten Netzwerk errechnet der Algorithmus von Dinic in Zeit
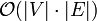 einen Maximalfluss, der genau die Größe der maximalen Paarung des ursprünglichen Graphen ist. Die lineare Laufzeit (gegenüber der im allgemeinen Fall quadratischen Laufzeit des Algorithmus von Dinic) ist hier auf die einheitlichen Kantengewichte zurückzuführen, die es dem Algorithmus ermöglichen, innerhalb einer Iteration alle Kanten gleichzeitig blockieren zu lassen.
einen Maximalfluss, der genau die Größe der maximalen Paarung des ursprünglichen Graphen ist. Die lineare Laufzeit (gegenüber der im allgemeinen Fall quadratischen Laufzeit des Algorithmus von Dinic) ist hier auf die einheitlichen Kantengewichte zurückzuführen, die es dem Algorithmus ermöglichen, innerhalb einer Iteration alle Kanten gleichzeitig blockieren zu lassen.
Wikimedia Foundation.