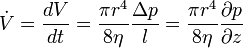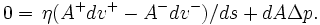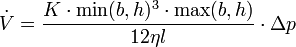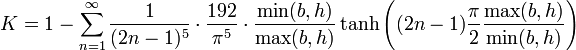Hagen-Poiseuille'sches Gesetz

Der Volumenstrom 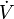$\dot V$, d. h. das geflossene Volumen V pro Zeiteinheit, bei einer laminaren Strömung einer homogenen viskosen Flüssigkeit durch ein Rohr (Kapillare) mit dem Radius r und der Länge l wird mit dem Gesetz von Hagen-Poiseuille (nach Gotthilf Heinrich Ludwig Hagen, 1797-1884; Jean Louis Marie Poiseuille, 1797-1869) beschrieben. Es lautet

$\dot V=\frac{dV}{dt} = \frac{\pi r^4}{8 \eta}\frac{\Delta p}{l} = \frac{\pi r^4}{8 \eta}\frac{\partial p}{\partial z}$

mit

Variable	Bedeutung	SI-Einheit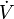
$\dot V$	Volumenstrom durch das Rohr	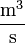$\frac{\rm m^3}{\rm s}$
r	Innenradius des Rohres	m
l	Länge des Rohres	m
η	dynamische Viskosität der strömenden Flüssigkeit	Pa·s
Δp	Druckdifferenz zwischen Anfang und Ende des Rohres	Pa
z	Flussrichtung

Dieses Gesetz folgt direkt aus dem stationären, parabolischen Strömungsprofil durch ein Rohr, das aus den Navier-Stokes-Gleichungen hergeleitet werden kann -- oder direkt aus der Definition der Viskosität, siehe unten. Bemerkenswert ist die Abhängigkeit des Volumendurchflusses von der vierten Potenz des Radius des Rohres. Dadurch hängt der Strömungswiderstand sehr stark vom Radius des Rohres ab, so würde beispielsweise eine Verringerung des Rohrdurchmessers um die Hälfte den Strömungswiderstand um das 16-fache erhöhen.

Herleitung

Hier ist die Überlegung, aus der das Hagen-Poiseuille-Gesetz und das ihr zugrundeliegende Strömungsprofil folgt: Bezeichne v(s) die Strömungsgeschwindigkeit bei Radius s eines kreisförmigen Rohres mit Radius r. Betrachten wir einen Strömungszylinder zwischen Radien s − ds / 2 und s + ds / 2, so gilt die Kraftgleichung

$0 = \,\eta (A^+dv^+ -A^-dv^- )/ds + dA \Delta p.$

Sie drückt aus, dass der Strömungszylinder sich mit konstanter Geschwindigkeit bewegt, die auf ihn einwirkende Gesamtkraft also null ist. Diese Kraft setzt sich aus drei Teilen zusammen:

(1) 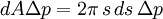$dA\Delta p = 2\pi \,s\, ds \,\Delta p$ ist die von der Druckdifferenz ΔP auf das Flächenstück 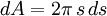$dA = 2\pi \,s\,ds$ erzeugte Kraft;

(2) 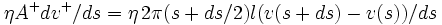$\eta A^+ dv^+/ds = \eta \,2\pi (s+ds/2) l (v(s+ds)-v(s)) / ds$ beschreibt die Reibung (Newtonsches Reibungsgesetz) des Strömungszylinders an dem nach außen benachbarten Strömungszylinder; die Geschwindigkeitsdifferenz von v(s + ds) − v(s) verteilt sich auf eine Schichtdicke ds und wirkt entlang der Fläche 2π(s + ds / 2)l;

(3) 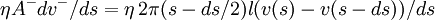$\eta A^- dv^-/ds = \eta \,2\pi (s-ds/2) l (v(s)-v(s-ds)) / ds$ beschreibt analog die Reibung am innen benachbarten Strömungszylinder.

Im Grenzübergang 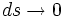$ds\to 0$ ergibt sich eine Differentialgleichung zweiter Ordnung für v(r), nämlich $v''(s)+v'(s)/s +\,\Delta p/\eta l=0$.

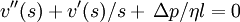Die Lösung muss die Randbedingung v(r) = 0 erfüllen und ist dadurch eindeutig bestimmt:

$v(s) = \frac{\Delta p}{4 \eta\, l} \,(r^2-s^2)$.

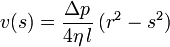Dies ist genau das genannte quadratische Strömungsprofil. Durch Integration folgt dann das Gesetz von Hagen-Poiseuille:

$\dot{V} = \int_0^{2\pi} \int_0^r v(s) s\,ds\,d\varphi = \frac{\pi r^4}{8\eta} \frac{\Delta p}{l}$

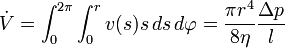
Nicht kreisförmige Kanalquerschnitte

Für einen Rechteck-Kanal mit den Abmessungen b und h lässt sich dieses Gesetz in der folgenden Form angeben:

$\dot V = \frac{K\cdot\min(b,h)^3\cdot\max(b,h)}{12\eta l}\cdot \Delta p$

Hierbei ist

$K=1-\sum_{n=1}^{\infty}\frac{1}{(2n-1)^5}\cdot\frac{192}{\pi^5}\cdot\frac{\min(b,h)}{\max(b,h)}\tanh\left((2n-1)\frac{\pi}{2}\frac{\max(b,h)}{\min(b,h)}\right)$

Die Abweichung vom exakten Wert bei Berechnung von K in erster Näherung (n=1) beträgt maximal 0,67 %, in zweiter Näherung 0,06 %, in dritter Näherung 0,01 %.

Einige Beispielwerte, berechnet in dritter Näherung:

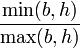
$\frac{\min(b,h)}{\max(b,h)}$	0	1/10	1/5	1/4	1/3	1/2	2/3	1
K	1	0,9370	0,8740	0,8425	0,7900	0,6861	0,5873	0,4218

Formeln für weitere Querschnittsformen werden z.B. in ^[1] hergeleitet.

Anwendungen

In der Praxis hat das Gesetz von Hagen-Poiseuille zum Beispiel Auswirkungen auf den Durchsatz des Blutes durch Blutgefäße bei Ablagerungen an der Gefäßwand. So bewirkt die Verengung einer Kapillare um 10% (1 bis max. 20 µm) einen Durchsatzrückgang um 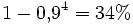$1 - 0{,}9^4 = 34\%$! Um also die Nährstoffversorgung zu gewährleisten, muss die Druckdifferenz, in diesem Fall also der Blutdruck, um 52% steigen, die Folge ist Bluthochdruck. Außerdem bildet das Gesetz von Hagen-Poiseuille die Grundlage einer Vielzahl von Modellgleichungen bei der Durchströmung von Schüttgütern.

Eingeschränkte Gültigkeit im Blut

Das Gesetz von Hagen-Poiseuille bezieht sich auf Newtonsche Flüssigkeiten. Bei Newtonschen Flüssigkeiten ist die Viskosität eine konstante Materialeigenschaft (und nur von der Temperatur abhängig). Ein Beispiel für eine solche Flüssigkeit ist Wasser. Das Blutplasma ist auch eine Newtonsche Flüssigkeit, nicht aber das Blut: Es ist eine inhomogene Suspension aus verschiedenen Zellen in Plasma. Hier ist die Viskosität von der Größe der Schubspannung (also der Strömungsgeschwindigkeit) abhängig. Weiterhin spielt auch die Deformierbarkeit der Erythrozyten eine Rolle. Diese können sich beispielsweise 'Geldrollenartig' in dünnen Gefäßen aggregieren.

Dieses spezielle Fachgebiet der Rheologie des Blutes wird als Hämorheologie (engl. hemorheology) bezeichnet.

Quellen

1. ↑ Henrik Bruus: Theoretical Microfluidics. Oxford University Press, 2008

Literatur

• Beitz, W.; Grote, K.-H. (Hrsg.): Dubbel. Taschenbuch für den Maschinenbau; 20. Aufl.; Springer-Verlag; Berlin, Heidelberg, New York (2001); ISBN 3-540-67777-1
• Hartnett, James P.; Kostic, Milivoje: "Heat Transfer to Newtonian and Non-Newtonian Fluids in Rectangular Ducts". In: Advances in Heat Transfer, Volume 19 (1989)
• Klinke, R.; Pape,H.-C.; Silbernagl, S: Physiologie; 5. Aufl.; Georg Thieme Verlag; Stuttgart, New York; ISBN 3-13-796005-3