Halber Tagbogen

Tagbögen der Sonne in Mitteleuropa, Blick nach Süden (schematisch; unter Horizont stark verzerrt)

Als Tagbogen wird in der Astronomie jener Teil der scheinbaren Sternbahn bezeichnet, der sich über dem mathematischen Horizont befindet.

Seine Länge entspricht der Zeit zwischen Aufgang und Untergang des Gestirns, wobei die Astronomische Refraktion i.a. nicht berücksichtigt wird (sie würde den Tagbogen um einige Minuten verlängern).
Der "wahre Tagbogen" berücksichtigt hingegen die Höhe des Landschaftshorizonts (bzw. auf dem Meer die Kimmtiefe).

Da die scheinbare Stern- bzw. Sonnenbahn im Meridian den Höchststand erreicht und somit Ost-West-symmetrisch ist, rechnet man in der Astronomie mit dem halben Tagbogen.

Der ganze Tagbogen sei daher als 2T bezeichnet; er hängt ab von der geographischen Breite B des Standortes und von der Deklination D des Gestirns und lässt sich mit Formeln der Sphärischen Trigonometrie einfach berechnen:

$\cos T = - \tan B \cdot \tan D$

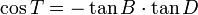
Wenn B oder D Null ist, ergibt sich cosT = 0 und T = 90° (oder 6 Stunden). Daher ist am Äquator der Tagbogen aller Gestirne (auch der Sonne) genau 12 Stunden. Hingegen ist er auf den Polen 24 Stunden oder 0 Stunden (es gibt dort keine Auf- und Untergänge, da Formel undefiniert).

In mittleren Breiten hat die Sonne Tagbögen (= Tageslänge) zwischen etwa 8 Stunden (Dezember/ Januar) und 16 Stunden (Juni/ Juli). Die zirkumpolaren Sterne (in der Nähe der Himmelspole, D > 90°-B ) sind 24 Stunden über dem Horizont, ihr Tagbogen ist daher 24 Stunden - unbeschadet der Tatsache, dass sie tagsüber von der Sonne überstrahlt werden.

Siehe auch:

• Sichtbarkeit, Sonnenaufgang, Sonnenuntergang, Sonnenstand
• Tagbeobachtung, Erdrotation, Astronomische Phänomenologie