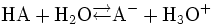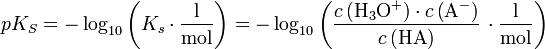Henderson-hasselbalch

Die Henderson-Hasselbalch-Gleichung, auch Puffergleichung genannt, geht auf Lawrence Joseph Henderson und Karl Albert Hasselbalch zurück. Henderson entwickelte seine nach ihm benannte Gleichung 1908. Hasselbalch konnte die Henderson-Gleichung experimentell beim menschlichen Blut bestätigen und schrieb die Gleichung 1916 um, um statt der Wasserstoffionenkonzentration den pH-Wert zu berechnen.

Die Gleichung beschreibt allgemein ein Säure-Base-Gleichgewicht einer teilweise dissoziierten, also schwachen Säure oder Base in wässriger Lösung. Mit Hilfe dieser Gleichung kann man den pH-Wert einer solchen Lösung berechnen.

Diese Gleichung leitet sich aus einer allgemeinen Säure-Base-Reaktion ab:

$\mathrm{HA + H_2O {\overrightarrow{\leftarrow}} A^- + H_3O^+}$

Hierbei ist HA eine allgemeine Säure und A^- eine allgemeine Base.

Die Säurekonstante K_S von HA ergibt sich aus dem Massenwirkungsgesetz. Nach Logarithmieren erhält man daraus die Henderson-Hasselbalch-Gleichung:

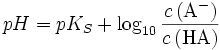$pH = pK_S + \log_{10} \frac{c \left( \mathrm{A^{-}} \right)}{c \left( \mathrm{HA}\right) }$ mit $pK_{S} = - \log_{10} \left( \mathrm{K_{S}} \, \cdot \mathrm{\frac{l}{mol}} \right)$.

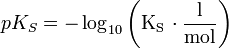Dabei wird die Definition des pK_S-Wertes benutzt

$pK_S = - \log_{10} \left( K_{s}\cdot\mathrm{\frac{l}{mol}} \right) = - \log_{10} \left( \frac{c \left( \mathrm{{H}_3O^{+}} \right) \cdot c \left( \mathrm{A^{-}} \right)}{c \left( \mathrm{HA} \right)} \, \cdot \mathrm{\frac{l}{mol}} \right)$

sowie des pH-Wertes

$pH = - \log_{10} \left[ c \left( \mathrm{{H}_{3}O^{+}} \right) \, \cdot \mathrm{\frac{l}{mol}} \right]$.

Im Pufferbereich der Titration entspricht das Verhältnis 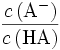$\frac{c \left( \mathrm{A^{-}} \right)}{c \left( \mathrm{HA}\right) }$ dem Verhältnis 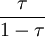$\frac{\tau}{1-\tau}$, so dass man schreiben kann:

$pH = pK_S + \log_{10} \frac{\tau}{1-\tau}$.

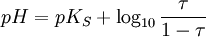τ ist dabei das Verhältnis der Stoffmenge (bzw. der Konzentration) der zugefügten Maßlösung zur Stoffmenge (bzw. der Konzentration) des zu bestimmenden Stoffes.^[1]

Im Bereich von τ=0 und τ=1 bzw. bei stärkerer Verdünnung (0,01 M) gilt diese Formel nicht mehr, da die geringe Protolyse von HA bzw. A^- mit dem Lösungsmittel bzw. die Autoprotolyse von Wasser um den pH von 7 (z.B. Phosphatpuffer) selbst für die Konzentrationsberechnung berücksichtigt werden müssen und es kann durchaus zu Abweichungen von 0,4 vom berechneten pH kommen. Für eine genaue Berechnung des pH-Wertes leite man sich die Gleichung nach dem Massenwirkungsgesetz her.

Diese Gleichung wird insbesondere bei der pH-Wert-Berechnung von Pufferlösungen verwendet, zu bedenken ist aber, dass zur Vereinfachung angenommen wird, die Basen- und Säurenkonzentration sei im Gleichgewicht gleich den Anfangskonzentrationen.

Siehe auch

• Dissoziation (Chemie)
• Chemisches Gleichgewicht

Einzelnachweise

1. ↑ Vorlesungsskript Analytische Chemie III der Universität Stuttgart