Heuristik der nächsten Einfügung
- Heuristik der nächsten Einfügung
-
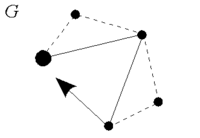
Nearest-Insertion-Heuristik
Die Nearest-Insertion-Heuristik (NEARIN), ist eine Einfüge-Heuristik und damit ein heuristisches Eröffnungsverfahren aus der Graphentheorie. Es dient zur Approximation einer guten Lösung des Problem des Handlungsreisenden; Ziel ist es also, eine möglichst kurze Rundreise durch alle Knoten des Graphen zu finden
Der Algorithmus wählt in jedem Schritt den von der zuletzt eingefügten Stadt am nächsten gelegenen Knoten aus. Dieser wird so in die vorhandene Teilroute eingebaut, dass die geringste Verlängerung der bisherigen Teilroute entsteht.
Der NEARIN-Algorithmus besteht also genaugenommen aus den zwei Teilen:
- nearest selection: für die Auswahl des nächsten Knotens
- cheapest insertion: für das Einfügen in den bestehenden Kreis
Die dabei entstehende Struktur entspricht immer einer transitiven Hülle. Dieses Verfahren wird bis zum n-ten Knoten fortgesetzt und entspricht der Komplexitätsklasse O(n2).
Als Varianten dieser treten die Farthest-Insertion-Heuristik, die Cheapest-Selection-Heuristik und die Random-Insertion-Heuristik auf.
siehe auch: Problem des Handlungsreisenden, Algorithmus von Floyd und Warshall, Liste von Algorithmen, Heuristik
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Farthest-Insertion-Heuristik — Die Farthest Insertion Heuristik (entfernteste Einfügung, FARIN) ist eine Einfüge Heuristik und damit ein heuristisches Eröffnungsverfahren aus der Graphentheorie. Es dient zur Approximation einer guten Lösung des Problem des Handlungsreisenden,… … Deutsch Wikipedia
Botenproblem — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein… … Deutsch Wikipedia
Euklidisches Traveling-Salesman-Problem — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein… … Deutsch Wikipedia
Handlungsreisendenproblem — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein… … Deutsch Wikipedia
Metrisches Traveling-Salesman-Problem — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein… … Deutsch Wikipedia
Problem des Handelsreisenden — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein … Deutsch Wikipedia
Rectilinieares Traveling-Salesman-Problem — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein … Deutsch Wikipedia
Rundfahrtproblem — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein … Deutsch Wikipedia
Rundreiseproblem — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein … Deutsch Wikipedia
Traveling-Salesman-Problem — Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen. Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein … Deutsch Wikipedia

