- Hopffaserung
-
Die Hopf-Faserung (nach Heinz Hopf) ist eine bestimmte Abbildung im mathematischen Teilgebiet der Topologie. Es handelt sich um eine Abbildung der 3-Sphäre, die man sich als den dreidimensionalen Raum zusammen mit einem unendlich fernen Punkt vorstellen kann, in die 2-Sphäre, also eine Kugeloberfläche:
Inhaltsverzeichnis
Beschreibung der Abbildung
Man erhält sie durch folgendes: Zuerst wird die S3 in den den C2eingebettet. Die Tupel
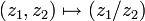 werden auf ihren Quotienten abgebildet. Danach bildet man den Punkt mit der Inversen Stereografische Projektion bzgl des Nordpoles auf die S2 ab. Um die Abbildung konkret anzugeben, gibt es viele verschiedene Möglichkeiten.
werden auf ihren Quotienten abgebildet. Danach bildet man den Punkt mit der Inversen Stereografische Projektion bzgl des Nordpoles auf die S2 ab. Um die Abbildung konkret anzugeben, gibt es viele verschiedene Möglichkeiten.Mit reellen Zahlen
Die Abbildung
mit
- y1 = 2(x1x3 + x2x4)
- y2 = 2(x2x3 − x1x4)
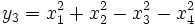
bildet die 3-Sphäre
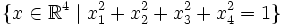 auf die 2-Sphäre
auf die 2-Sphäre 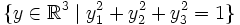 ab. Diese Einschränkung ist die Hopf-Abbildung.
ab. Diese Einschränkung ist die Hopf-Abbildung.Mit komplexen Zahlen
Die 3-Sphäre werde als die Teilmenge
des zweidimensionalen komplexen Raums aufgefasst, die 2-Sphäre als riemannsche Zahlenkugel. Dann ist die Hopf-Abbildung durch
gegeben. Fasst man die riemannsche Zahlenkugel als projektive Gerade
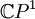 auf, so kann man die Abbildung unter Verwendung homogener Koordinaten auch als
auf, so kann man die Abbildung unter Verwendung homogener Koordinaten auch alsschreiben.
Mit Liegruppen
Die 3-Sphäre ist diffeomorph zur Liegruppe Spin(3), die als Überlagerung der Drehgruppe SO(3) auf der 2-Sphäre operiert.
Eigenschaften
- Die Hopf-Abbildung ist ein Faserbündel mit Faser S1 (sogar ein S1-Hauptfaserbündel).
- Die Hopf-Abbildung erzeugt die Homotopiegruppe
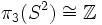 .
.
Verallgemeinerungen
Die oben angegebene Beschreibung mithilfe komplexer Zahlen kann auch stattdessen mit Quaternionen oder mit Cayley-Zahlen durchgeführt werden; man erhält dann Faserungen
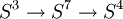 bzw.
bzw. 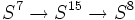 ,
,
die ebenfalls als Hopf-Faserungen bezeichnet werden.
Geschichte
Heinz Hopf gab diese Abbildung 1931 in seiner Arbeit Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche an und zeigte, dass sie nicht nullhomotop ist (genauer: dass ihre Hopf-Invariante gleich 1 ist).
Literatur
- Heinz Hopf: Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche. Math. Ann. 104 (1931), 637–665 (PDF)
Wikimedia Foundation.

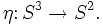
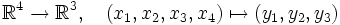
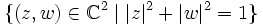
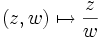
![(z,w)\mapsto[z:w]](/pictures/dewiki/100/db2d7ed3fda72f8f706889c9c8562a1f.png)