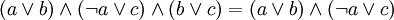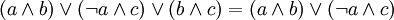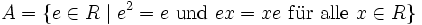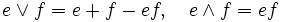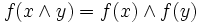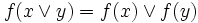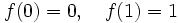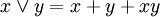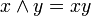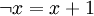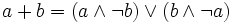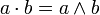- Huntingtonsches Axiomensystem
-
In der Mathematik ist eine boolesche Algebra (oder ein boolescher Verband) eine spezielle algebraische Struktur, die die Eigenschaften der logischen Operatoren UND, ODER, NICHT sowie die Eigenschaften der mengentheoretischen Verknüpfungen Durchschnitt, Vereinigung, Komplement verallgemeinert. Gleichwertig zu booleschen Algebren sind boolesche Ringe, die von UND und ENTWEDER-ODER (exclusiv-ODER) beziehungsweise Durchschnitt und symmetrischer Differenz ausgehen.
Operatoren 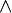
UND 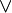
ODER 
NICHT Die Operatoren boolescher Algebren werden verschiedenartig notiert. Bei der logischen Interpretation als Konjunktion, Disjunktion und Negation schreibt man sie als UND, ODER, NICHT bzw. AND, OR, NOT und kürzt sie mit
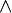 ,
, 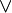 und
und  ab. Bei der mengentheoretischen Interpretation als Durchschnitt, Vereinigung und Komplement werden sie als
ab. Bei der mengentheoretischen Interpretation als Durchschnitt, Vereinigung und Komplement werden sie als 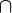 ,
, 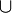 und
und 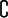 geschrieben. In Schaltkreisen benutzt man oft die definierbaren Verknüpfungen NAND (NOT AND), NOR (NOT OR) und XOR (EXCLUSIVE OR). Mathematiker schreiben gelegentlich + für ODER und · für UND (wegen ihrer Ähnlichkeit zur Addition und Multiplikation anderer algebraischer Strukturen) und stellen NICHT mit einem Überstrich oder einer Tilde ~ dar.
geschrieben. In Schaltkreisen benutzt man oft die definierbaren Verknüpfungen NAND (NOT AND), NOR (NOT OR) und XOR (EXCLUSIVE OR). Mathematiker schreiben gelegentlich + für ODER und · für UND (wegen ihrer Ähnlichkeit zur Addition und Multiplikation anderer algebraischer Strukturen) und stellen NICHT mit einem Überstrich oder einer Tilde ~ dar.In diesem Artikel werden die Operatoren
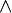 ,
, 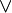 und
und  verwendet.
verwendet.Inhaltsverzeichnis
Zur Geschichte
Die boolesche Algebra ist nach George Boole benannt, da sie auf dessen Logikkalkül von 1847 zurückgeht, in dem er erstmals algebraische Methoden in der Klassenlogik und Aussagenlogik anwandte. Ihre heutige Form verdankt sie der Weiterentwicklung durch Mathematiker wie John Venn, W. Stanley Jevons, Charles Peirce, Ernst Schröder und Giuseppe Peano. In Booles originaler Algebra entspricht die Multiplikation dem UND, die Addition dagegen weder dem exklusiven ENTWEDER-ODER noch dem inklusiven ODER ("mindestens eines von beiden ist wahr"). Die genannten Boole-Nachfolger gingen dagegen vom inklusiven ODER aus: Schröder entwickelte 1877 das erste formale Axiomensystem einer booleschen Algebra in additiver Schreibweise, Peano brachte es 1888 in die heutige Form (siehe unten) und führte dabei die Symbole
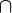 und
und 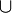 ein. Das aussagenlogische ODER-Zeichen
ein. Das aussagenlogische ODER-Zeichen 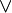 stammt von Russell 1906; [1] Arend Heyting führte 1930 die Symbole
stammt von Russell 1906; [1] Arend Heyting führte 1930 die Symbole 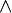 und
und  ein. Den Namen „boolesche Algebra“ bzw. „boolean algebra“ prägte Henry Maurice Sheffer erst 1913. Das exklusive ENTWEDER-ODER, das Booles originaler Algebra näher kommt, legte erst Ivan Ivanovich Žegalkin 1927 dem booleschen Ring zugrunde, dem Marshall Harvey Stone 1936 den Namen gab. 1940 benutzte Claude Shannon boolesche Algebren erstmals zur Beschreibung elektrischer Schaltungen.
ein. Den Namen „boolesche Algebra“ bzw. „boolean algebra“ prägte Henry Maurice Sheffer erst 1913. Das exklusive ENTWEDER-ODER, das Booles originaler Algebra näher kommt, legte erst Ivan Ivanovich Žegalkin 1927 dem booleschen Ring zugrunde, dem Marshall Harvey Stone 1936 den Namen gab. 1940 benutzte Claude Shannon boolesche Algebren erstmals zur Beschreibung elektrischer Schaltungen.Definition
Eine boolesche Algebra ist ein distributiver komplementärer Verband.
Diese Definition geht nur von den Verknüpfungen
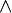 und
und 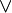 aus und umfasst die Existenz von 0, 1 und
aus und umfasst die Existenz von 0, 1 und  und die unabhängigen Axiome (1)(1’)(2)(2’)(11)(11’)(4)(9)(9’) des gleichwertigen redundanten Axiomensystems von Peano mit zusätzlichen ableitbaren Axiomen; dieses charakterisiert eine boolesche Algebra als Menge mit Nullelement 0 und Einselement 1, auf der die zweistelligen Verknüpfungen
und die unabhängigen Axiome (1)(1’)(2)(2’)(11)(11’)(4)(9)(9’) des gleichwertigen redundanten Axiomensystems von Peano mit zusätzlichen ableitbaren Axiomen; dieses charakterisiert eine boolesche Algebra als Menge mit Nullelement 0 und Einselement 1, auf der die zweistelligen Verknüpfungen 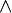 und
und 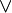 und eine einstellige Verknüpfung
und eine einstellige Verknüpfung  definiert sind, durch folgende Axiome (originale Nummerierung von Peano):
definiert sind, durch folgende Axiome (originale Nummerierung von Peano):Kommutativgesetze (1) 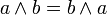
(1’) 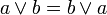
Assoziativgesetze (2) 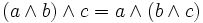
(2’) 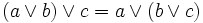
Idempotenzgesetze (3) 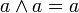
(3’) 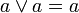
Distributivgesetze (4) 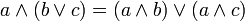
(4’) 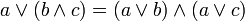
Neutralitätsgesetze (5) 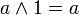
(5’) 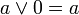
Extremalgesetze (6) 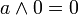
(6’) 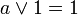
Doppelnegationsgesetz (Involution) (7) 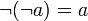
De Morgansche Gesetze (8) 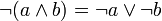
(8’) 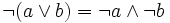
Komplementärgesetze (9) 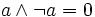
(9’) 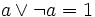
Dualitätsgesetze (10) 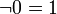
(10’) 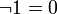
Absorptionsgesetze (11) 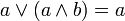
(11’) 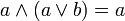
Jede Formel in einer booleschen Algebra hat eine duale Formel, die durch Ersetzung von 0 durch 1 und
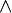 durch
durch 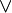 und umgekehrt entsteht. Ist die eine Formel gültig, dann ist es auch ihre duale Formel, wie im Peano-Axiomensystem jeweils (n) und (n').
und umgekehrt entsteht. Ist die eine Formel gültig, dann ist es auch ihre duale Formel, wie im Peano-Axiomensystem jeweils (n) und (n').Man beachte, dass die Komplemente nichts mit inversen Elementen zu tun haben, denn die Verknüpfung eines Elementes mit seinem Komplement liefert das neutrale Element der anderen Verknüpfung.
Auf einer booleschen Algebra ist wie in jedem Verband durch
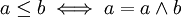 eine partielle Ordnung definierbar; bei ihr haben je zwei Elemente ein Supremum und ein Infimum. Bei der mengentheoretischen Interpretation ist
eine partielle Ordnung definierbar; bei ihr haben je zwei Elemente ein Supremum und ein Infimum. Bei der mengentheoretischen Interpretation ist 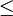 gleichbedeutend zur Teilmengenordnung
gleichbedeutend zur Teilmengenordnung 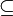 .
.Beispiele
Zweielementige boolesche Algebra
Die wichtigste boolesche Algebra hat nur die zwei Elemente 0 und 1. Die Verknüpfungen sind wie folgt definiert:
Konjunktion 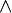
0 1 0 0 0 1 0 1 Disjunktion 
0 1 0 0 1 1 1 1 Negation 
0 1 1 0 Diese Algebra hat Anwendungen in der Aussagenlogik, wo 0 als "falsch" und 1 als "wahr" interpretiert werden. Die Verknüpfungen
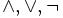 entsprechen den logischen Verknüpfungen UND, ODER, NICHT. Ausdrücke in dieser Algebra heißen boolesche Ausdrücke.
entsprechen den logischen Verknüpfungen UND, ODER, NICHT. Ausdrücke in dieser Algebra heißen boolesche Ausdrücke.Auch für digitale Schaltungen wird diese Algebra verwendet und als Schaltalgebra bezeichnet. Hier entsprechen 0 und 1 zwei Spannungszuständen in der Schalterfunktion von AUS und AN. Das Eingangs-Ausgangs-Verhalten jeder möglichen digitalen Schaltung kann durch einen booleschen Ausdruck modelliert werden.
Die zweielementige boolesche Algebra ist auch wichtig für die Theorie allgemeiner boolescher Algebren, da jede Gleichung, in der nur Variablen, 0 und 1 durch
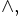
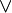 und
und  verknüpft sind, genau dann in einer beliebigen booleschen Algebra für jede Variablenbelegung erfüllt ist, wenn sie in der zweielementigen Algebra für jede Variablenbelegung erfüllt ist (was man einfach durchtesten kann). Zum Beispiel gelten die folgenden beiden Aussagen (Konsensusregeln, engl.: Consensus Theorems) über jede boolesche Algebra:
verknüpft sind, genau dann in einer beliebigen booleschen Algebra für jede Variablenbelegung erfüllt ist, wenn sie in der zweielementigen Algebra für jede Variablenbelegung erfüllt ist (was man einfach durchtesten kann). Zum Beispiel gelten die folgenden beiden Aussagen (Konsensusregeln, engl.: Consensus Theorems) über jede boolesche Algebra:In der Aussagenlogik nennt man diese Regeln Resolutionsregeln.
Mengenalgebra
Die Potenzmenge P(S) einer Menge S wird mit Durchschnitt und Vereinigung zu einer booleschen Algebra. Dabei ist 0 die leere Menge und 1=S und die Negation das Komplement; der Sonderfall S=0 ergibt die einelementige Potenzmenge mit 1=0. Auch jeder S enthaltende, bezüglich Vereinigung und Komplement abgeschlossene Teilbereich der Potenzmenge von S ist eine boolesche Algebra, die als Teilmengenverband oder Mengenalgebra bezeichnet wird. Der Darstellungssatz von Stone besagt, dass jede boolesche Algebra isomorph (s.u.) zu einer Mengenalgebra ist. Daraus folgt, dass die Mächtigkeit jeder endlichen booleschen Algebra eine Zweierpotenz ist.
Andere Beispiele
Die Menge aller endlichen oder koendlichen Teilmengen von
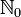 bildet mit Durchschnitt und Vereinigung eine boolesche Algebra.
bildet mit Durchschnitt und Vereinigung eine boolesche Algebra.Für jede natürliche Zahl n ist die Menge aller positiven Teiler von n mit den Verknüpfungen ggT und kgV ein distributiver beschränkter Verband. Dabei ist 1 das Nullelement und n das Einselement. Der Verband ist boolesch genau dann, wenn n quadratfrei ist. Dieser Verband heißt Teilerverband von n.
Für jeden topologischen Raum X ist die Menge aller offenen abgeschlossenen Teilmengen eine boolesche Algebra mit Durchschnitt und Vereinigung.
Ist R ein Ring mit Einselement, dann definieren wir die Menge
aller idempotenten Elemente des Zentrums. Mit den Verknüpfungen
wird A zu einer booleschen Algebra.
Ist H ein Hilbertraum und P(H) die Menge der Orthogonalprojektionen auf H. Definiert man für zwei Orthogonalprojektionen P und Q
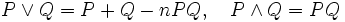 , wobei n gleich 1 oder 2 sein soll. In beiden Fällen wird P(H) zu einer booleschen Algebra. Der Fall n=2 ist in der Spektraltheorie von Bedeutung.
, wobei n gleich 1 oder 2 sein soll. In beiden Fällen wird P(H) zu einer booleschen Algebra. Der Fall n=2 ist in der Spektraltheorie von Bedeutung.Siehe auch Boolesche Funktion.
Homomorphismen
Ein Homomorphismus zwischen booleschen Algebren A,B ist ein Verbandshomomorphismus
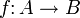 , der 0 auf 0 und 1 auf 1 abbildet, d.h. für alle
, der 0 auf 0 und 1 auf 1 abbildet, d.h. für alle 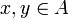 gilt:
gilt:Es folgt daraus, dass
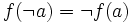 für alle a aus A. Die Klasse aller booleschen Algebren wird mit diesem Homomorphismenbegriff eine Kategorie. Ist ein Homomorphismus f zusätzlich bijektiv, dann heißt f Isomorphismus, und A und B heißen isomorph.
für alle a aus A. Die Klasse aller booleschen Algebren wird mit diesem Homomorphismenbegriff eine Kategorie. Ist ein Homomorphismus f zusätzlich bijektiv, dann heißt f Isomorphismus, und A und B heißen isomorph.Boolesche Ringe
Als boolesche Ringe gelten seit Stone alle kommutativen Ringe mit Einselement, die zusätzlich das Idempotenzgesetz
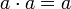 erfüllen. Die Addition im booleschen Ring entspricht bei der mengentheoretischen Interpretation der symmetrischen Differenz und bei aussagenlogischer Interpretation der Alternative ENTWEDER-ODER (exclusiv-ODER, XOR); die Multiplikation entspricht der Durchschnittsbildung beziehungsweise der Konjunktion UND.
erfüllen. Die Addition im booleschen Ring entspricht bei der mengentheoretischen Interpretation der symmetrischen Differenz und bei aussagenlogischer Interpretation der Alternative ENTWEDER-ODER (exclusiv-ODER, XOR); die Multiplikation entspricht der Durchschnittsbildung beziehungsweise der Konjunktion UND.Boolesche Ringe sind stets selbstinvers, denn es gilt
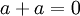 und
und 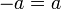 , so dass die Inversen-Operation definierbar ist. Wegen dieser Eigenschaft besitzen sie auch, falls 1 und 0 verschieden sind, stets die Charakteristik 2. Der kleinste solche boolesche Ring ist zugleich ein Körper mit folgenden Verknüpfungstafeln:
, so dass die Inversen-Operation definierbar ist. Wegen dieser Eigenschaft besitzen sie auch, falls 1 und 0 verschieden sind, stets die Charakteristik 2. Der kleinste solche boolesche Ring ist zugleich ein Körper mit folgenden Verknüpfungstafeln:
0 1 0 0 0 1 0 1 + 0 1 0 0 1 1 1 0 Der Potenzreihen-Ring modulo
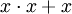 über diesem Körper ist ebenfalls ein boolescher Ring, denn
über diesem Körper ist ebenfalls ein boolescher Ring, denn 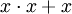 wird mit
wird mit 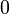 identifiziert und liefert die Idempotenz. Diese Algebra benützte bereits Žegalkin 1927 als Variante der originalen Algebra von Boole, der den Körper der reellen Zahlen zugrunde legte, welcher noch keinen booleschen Ring ergibt.
identifiziert und liefert die Idempotenz. Diese Algebra benützte bereits Žegalkin 1927 als Variante der originalen Algebra von Boole, der den Körper der reellen Zahlen zugrunde legte, welcher noch keinen booleschen Ring ergibt.Die Kategorien boolescher Ringe und boolescher Algebren sind isomorph. Denn jeder boolesche Ring
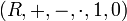 wird zu einer booleschen Algebra
wird zu einer booleschen Algebra 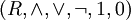 durch folgende Definitionen:
durch folgende Definitionen:Umgekehrt wird jede boolesche Algebra
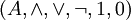 zu einem booleschen Ring
zu einem booleschen Ring 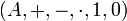 durch folgende Definitionen:
durch folgende Definitionen:Ferner ist eine Abbildung
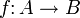 genau dann ein Homomorphismus boolescher Algebren, wenn sie ein Homomorphismus boolescher Ringe ist.
genau dann ein Homomorphismus boolescher Algebren, wenn sie ein Homomorphismus boolescher Ringe ist.Siehe auch
- Bitweiser Operator
- Boolescher Operator
- Heyting-Algebra
- Logische Verknüpfung
- Logikgatter
- Halbring
- Boolescher Differentialkalkül
Literatur
- Ernst Schröder: Der Operationskreis des Logikkalkuls. Leipzig 1877
- Giuseppe Peano: Calcolo geometrico. 1888. In: G. Peano, Opere scelte II. Rom 1958, Seiten 3-19.
- Marshall Harvey Stone: The Theorie of Representations for Boolean Algebras. In: Transactions of the American Mathematical Society Band 40, 1936, Seiten 37-111.
Weblinks
- J. Donald Monk: „The Mathematics of Boolean Algebra“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
Einzelnachweise
- ↑ Bertrand Russell: The Theory of Implication. In: American Journal of Mathematics. Band 28, 1906, Seiten 159-202.
Wikimedia Foundation.