Hyperkomplexe Zahlen

Hyperkomplexe Zahlen sind Verallgemeinerungen der komplexen Zahlen. In diesem Artikel werden hyperkomplexe Zahlen als algebraische Struktur betrachtet. Manchmal werden auch die Quaternionen als die hyperkomplexen Zahlen bezeichnet.

Inhaltsverzeichnis

1 Definition
2 Konjugation
3 Beispiele
4 Bemerkungen
5 Verwandte Themen
6 Literatur

Definition

Hyperkomplexe Zahlen bilden algebraische Strukturen über den reellen Zahlen mit Addition und Multiplikation. Man fordert die folgenden Eigenschaften:

Für die Addition gelten das Kommutativgesetz und das Assoziativgesetz.
Die Addition ist invertierbar.
Das linksseitige und das rechtsseitige Distributivgesetz gilt.

Die Multiplikation von hyperkomplexen Zahlen ist bilinear über den reellen Zahlen, also gilt (ax)(by) = ab (xy) für alle a,b 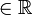$\in \mathbb{R}$ und x,y hyperkomplexe Zahlen.

Andere Eigenschaften werden nicht gefordert:

Für die Multiplikation von hyperkomplexen Zahlen braucht weder das Kommutativgesetz noch das Assoziativgesetz zu gelten.
Die Multiplikation braucht nicht nullteilerfrei zu sein.
Elemente müssen bzgl. der Multiplikation nicht notwendig invertierbar sein.

Konjugation

Hyperkomplexe Zahlen lassen sich wie folgt als Summe darstellen:

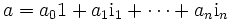$a = a_01 + a_1\mathrm i_1 + \cdots + a_n\mathrm i_n$ .

Die Größen $i k$ heißen imaginäre Einheiten. Die zu $a$ konjugierte Zahl entsteht, indem alle imaginären Einheiten durch ihr negatives ersetzt werden ( 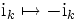$\mathrm i_k \mapsto -\mathrm i_k$ ). Die zu $a$ konjugiert komplexe Zahl wird durch 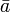$\bar a$ oder $a *$ dargestellt. Ihre Summendarstellung ist

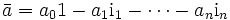$\bar a = a_01 - a_1\mathrm i_1 - \cdots - a_n\mathrm i_n$ .

Die Konjugation ist eine Involution auf den hyperkomplexen Zahlen, das heißt, dass

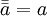$\bar{\bar a} = a$ .

Beispiele

Die Komplexen Zahlen

Die Komplexen Zahlen $\mathbb{C}$ sind ein hyperkomplexes Zahlensystem, das durch

$z = a + b i$ mit $i 2 = - 1$

definiert ist.

Die binären Zahlen

Die binären Zahlen sind definiert durch

z = a + bE mit $E 2 = 1$ .

Die dualen Zahlen

Die dualen Zahlen sind definiert durch

$z = a + b Ω$ mit $Ω 2 = 0$ .

Beachte, dass sie nichts mit Dualzahlen zu tun haben.

Die Quaternionen

Die Quaternionen (Symbol oft 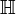$\mathbb{H}$ nach ihrem Entdecker W. R. Hamilton) bilden eine vierdimensionale $\mathbb{R}$ -Algebra mit Division und assoziativer (aber nicht kommutativer) Multiplikation. Es handelt sich bei den Quaternionen also um einen Schiefkörper.

Die Oktonionen

Die Oktonionen (Symbol 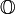$\mathbb{O}$ , auch Oktaven genannt) sind achtdimensionale hyperkomplexe Zahlen mit Division und alternierender Multiplikation.

Die Sedenionen

Die Sedenionen (Symbol 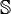$\mathbb{S}$ ) sind sechzehndimensionale hyperkomplexe Zahlen. Ihre Multiplikation ist weder kommutativ, assoziativ oder alternativ. Auch besitzen sie keine Division; stattdessen haben sie Nullteiler.

Bemerkungen

Mit dem Verdopplungsverfahren (auch als Cayley-Dickson-Verfahren bekannt) lassen sich neue hyperkomplexe Zahlensysteme erzeugen, die doppelt so viele Dimensionen wie das Ausgangszahlensystem haben.

Jede Clifford-Algebra ist ein assoziatives hyperkomplexes Zahlensystem.

Literatur

I. L. Kantor, A. S. Solodownikow: Hyperkomplexe Zahlen. BSG B. G. Teubner Verlagsgesellschaft, Leipzig, 1978.

Wikimedia Foundation.

Игры ⚽ Нужен реферат?

Schlagen Sie auch in anderen Wörterbüchern nach:

hyperkomplexe Zahlen — hyperkomplẹxe Zahlen, Mathematik: Quaternionen … Universal-Lexikon
Hyperkomplexe Zahl — Hyperkomplexe Zahlen sind Verallgemeinerungen der komplexen Zahlen. In diesem Artikel werden hyperkomplexe Zahlen als algebraische Struktur betrachtet. Manchmal werden auch die Quaternionen als die hyperkomplexen Zahlen bezeichnet.… … Deutsch Wikipedia
Irreelle Zahlen — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… … Deutsch Wikipedia
Komplexe Zahlen — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… … Deutsch Wikipedia
Hamilton-Zahlen — Gedenktafel an der Broom Bridge in Dublin, wo William Rowan Hamilton die Multiplikationsregeln im Oktober 1843 spontan in den Stein ritzte. Die Quaternionen (von lat. quaternio „Vierheit“) sind eine Erweiterung der reellen Zahlen, ähnlich den… … Deutsch Wikipedia
Duale Zahlen — Im mathematischen Teilgebiet der algebraischen Geometrie ist der Ring der dualen Zahlen über einem Körper ein algebraisches Objekt, das eng mit dem Begriff des Tangentialvektors zusammenhängt. Dieser Artikel beschäftigt sich mit kommutativer… … Deutsch Wikipedia
Binäre Zahlen — Definition Die Binären Zahlen (englisch split complex numbers oder hyperbolic numbers (zur Begründung s. unten)) bilden eine zweidimensionale hyperkomplexe Algebra über dem Körper der reellen Zahlen; wie die Komplexen Zahlen wird diese Algebra… … Deutsch Wikipedia
Komplexe Zahlen — (komplexe Größen), Zahlen, die aus mehreren nicht durch einander meßbaren Einheiten (s. Einheit) zusammengesetzt sind. In diesem Sinn ist z. B. die Summe aus 3 Äpfeln und 2 Birnen eine komplexe Zahl. In der Mathematik hat man sich zur Einführung… … Meyers Großes Konversations-Lexikon
Biquaternionen — Die Biquaternionen sind ein hyperkomplexes Zahlensystem, das von William Kingdon Clifford in der zweiten Hälfte des 19. Jahrhunderts beschrieben wurde. Vor Clifford hatte Arthur Cayley bereits die Quaternionen mit komplexen Koeffizienten (also… … Deutsch Wikipedia
Zahlbereich — Die Artikel Zahl und Zahlenmenge überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach… … Deutsch Wikipedia

Academic dictionaries and encyclopedias

Hyperkomplexe Zahlen

Inhaltsverzeichnis

Definition

Konjugation