Indische Ziffern

Arabische/Indische Ziffern

Entwicklung der arabischen Ziffern

Entwicklung der arabischen Ziffern in Europa; Legende (en, fr) nach Klick

Die Indischen Ziffern sind eine Zahlschrift, in der Zahlen positionell auf der Grundlage eines Dezimalsystems mit neun aus der altindischen Brahmi-Schrift herzuleitenden Zahlzeichen und einem eigenen, oft als Kreis oder Punkt geschriebenen Zeichen für die Null dargestellt werden.

Begriffsverwendung im Deutschen

Als indische Ziffern im engeren Sinn bezeichnet man in heutiger deutscher Fachsprache zunächst nur die in Indien selbst entstandenen und gebrauchten Ausprägungen dieser Zahlschrift, in einem weiteren Sinn auch deren Adaptionen in anderen Schriftkulturen, soweit sie auf direktes indisches Vorbild zurückgehen. Hierzu zählen auch die im frühen Mittelalter nach indischen Vorbild entstandenen arabischen oder indisch-arabischen (auch indo-arabisch oder hindu-arabisch genannten) Ziffern, die ihrerseits seit dem 12. Jahrhundert (mit Vorläufern seit dem 10. Jahrhundert) von der lateinischen und griechischen Schriftkultur Europas adaptiert wurden und sich von Westeuropa aus in ihrer seit dem Spätmittelalter vereinheitlichten Schreibform durch den Buchdruck als heute weltweit vorherrschender oder neben lokal dominierenden anderen Zahlschriften zumindest weithin voraussetzbarer Standard etablierten.

Ein generischer Oberbegriff, der sowohl das im engeren Sinn indische als auch alle übrigen daraus direkt oder indirekt abgeleiteten und dem Typ nach wesentlich gleichartigen Ziffernsysteme bezeichnet, ist in der deutschen Fachsprache nicht allgemein etabliert, am ehesten kommt hierfür aber der Begriff "indisch-arabische" Ziffern infrage, sofern er in additiver Bedeutung (indisch und arabisch) und nicht in kontrastiver Bedeutung (arabisch adaptiert und vermittelt) als Gegenbegriff zu "indisch" gemeint ist. In der deutschen Allgemeinsprache sind die Begriffe "indische" und "indisch-arabische Ziffern" weitgehend unbekannt, dort ist nur "arabische Ziffern" für das heute gebräuchliche Ziffernsystem etabliert, und dieser Begriff wird dann auch in fachsprachlichen Kontexten oft in erweiterter Bedeutung unter Vernachlässigung der genuin indischen und der nicht arabisch geprägten Varianten als generischer Oberbegriff gebraucht.

Entstehung und Ausbreitung

Indien – vom Anfang zur Vollendung

Am Beginn der Entwicklung der indischen Ziffern standen die Brahmi-Ziffern.

शून्य (śūnya) – null

Unter dem Wort śūnya (Sanskrit, n., शून्य, die Leere, das Nichts, das Nichtvorhandensein) wurde die Zahl Null geboren. Die philosophische Grundlage dafür war wahrscheinlich das buddhistische Konzept śūnyatā (Sanskrit, f., शून्यता, die Leerheit, die illusorische Natur der Phänomene) wie es Nāgārjuna (2. Jh. n. Chr.) in der Lehre von der Leerheit (śūnyatāvāda) beschrieben hat.^[1] Als weitere Bezugsquelle kommt die Schreibung des Wertes Null als Leerzeichen durch die Babylonier ab dem 6. Jahrhundert v. Chr. in Betracht.^[2]

Brahmasphutasiddhanta

628 n. Chr. verfasste der indische Astronom und Mathematiker Brahmagupta das Brahmasphutasiddhanta (Der Anfang des Universums). Es ist, wenn man vom Zahlensystem der Maya absieht, der früheste bekannte Text, in dem die Null als vollwertige Zahl behandelt wird. Darüber hinaus stellte Brahmagupta in diesem Werk Regeln für die Arithmetik mit negativen Zahlen und mit der Zahl 0 auf, die schon weitgehend unserem modernen Verständnis entsprechen. Der größte Unterschied bestand darin, dass Brahmagupta auch die Division durch 0 zuließ, während in der modernen Mathematik Quotienten mit dem Divisor 0 nicht definiert sind.

Weltweite Verbreitung

Die weltweite Verbreitung der indischen Ziffern ging nicht direkt mit einer weltweiten Verbreitung des Brahmasphutasiddhanta einher, sondern benötigte einige Zwischenschritte.

Arabische Verbreitung

Zwischen 640 und 644 besetzen die Araber den Irak und Persien.

Eine Seite aus Al-Chwarizmis al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala

al-Kitāb al-muchtaṣar fī ḥisāb al-dschabr wa-l-muqābala

Um 825 schreibt der persische Mathematiker, Astronom und Geograph al-Chwārizmī sein Werk al-Kitāb al-muchtaṣar fī ḥisāb al-dschabr wa-l-muqābala (Das zusammengefasste Buch über Algebra und Quotientenrechnen) das auf dem Brahmasphutasiddhanta basiert.

Ab hier wird die Null als ṣifr (arabisch ‏الصفر‎, DMG aṣ-ṣifr, „null, nichts“ vom Verb ṣafira "leer sein") bezeichnet – eine Lehnübersetzung des Wortes śūnya.

Kitab al-jabr wa’l-muqabala

Der ägyptische Mathematiker Abū Kāmil (ca. 850 bis ca. 930, auch bekannt als al-Hasib al-Misri, der »ägyptische Rechner«) führte in seiner Algebra (Kitab al-jabr wa’l-muqabala) die Algebra al-Khwārizmīs weiter.
Das Buch ist nur in lateinischer und hebräischer Übersetzung erhalten, das arabische Original ist verloren. Die Algebra wurde von Fibonacci und al Karagi benutzt.

Der Sprung ins Abendland

Liber abaci

Der Italiener Leonardo Fibonacci folgt um 1192 seinem Vater ins arabisch besetzte Algerien und lernt Abū Kāmils Algebra kennen. 1202 vollendet Fibonacci das Liber abaci, in welchem er unter anderem die indischen Ziffern vorstellt und diese in der Tat als »indische Ziffern« und nicht als »arabische Ziffern« bezeichnet.

Typographische Varianten

Dieser Abschnitt ist der historischen Entstehung der verschiedenen typographischen Varianten und den heute gebräuchlichen Formen der Indischen Ziffern gewidmet.

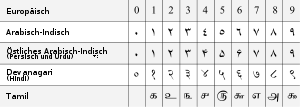
Indische Varianten

Da in Indien bereits vor einigen tausend Jahren astronomische Beobachtungen systematisch und auf einem hohen Niveau betrieben worden sind, wurden große Zahlen benötigt – Lakh [lakʰ] und Crore [kror] (Hindi: करोड़, karoṛ). Ein Lakh entspricht 100.000, ein Crore sind 100 Lakh, entspricht also 10.000.000. Diese Zahlen haben sich, obwohl sie offiziell gegen das Tausendersystem ausgetauscht wurden, gehalten und sind noch heute im allgemeinen Sprachgebrauch zu finden.

Arabische Varianten

Im Unterschied zur Richtung der arabischen Schrift (von rechts nach links) werden die indischen Zahlen auch in arabischen Texten entsprechend ihrer historischen Herkunft von links nach rechts dargestellt: Einer ganz rechts, links gefolgt von Zehnern, Hundertern, Tausendern usw.

Bevor die Araber das indische Stellenwertsystem übernahmen, benutzten sie für die Darstellung von Zahlen die Buchstaben des Alphabets, denen nebst dem Lautwert jeweils auch ein Zahlenwert zugewiesen war (vgl. Arabisches Alphabet). Diese Möglichkeit wird auch heute teilweise noch in bestimmten Situationen angewendet, ganz so, wie auch wir in bestimmten Situationen noch Römische Zahlen benutzen.

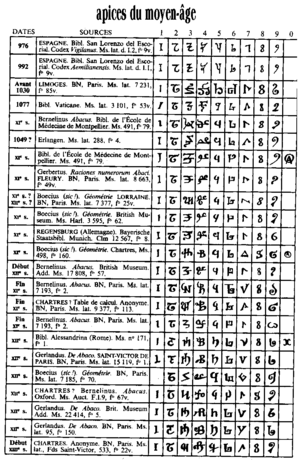
Europäische Varianten

Versalziffern und Mediävalziffern

In Europa lassen sich vor allem zwei Darstellungsformen von Ziffern unterscheiden: Versalziffern und Mediävalziffern.

Die meistverbreitete Variante sind Versalziffern: alle Ziffern haben die gleiche Höhe (die der Großbuchstaben). Um einen sauberen Tabellensatz zu ermöglichen, sind Versalziffern meistens alle gleich breit, nämlich so breit wie ein Halbgeviert. Diese Variante wird auch als Tabellenziffern bezeichnet, weniger gebräuchlich sind versale Proportionalziffern, bei denen insbesondere die 1 schmaler als die anderen Ziffern ist. Der Nachteil der Versalziffern ist, dass sie im Lauftext einen optischen Fremdkörper bilden und dass bei einigen Ziffern (etwa bei der 1) auch der Buchstabenabstand nicht stimmt.

Aus diesem Grund verfügen gut ausgebaute Schriften über einen zweiten Satz Ziffern, die Mediävalziffern. Diese haben wie Kleinbuchstaben Ober- und Unterlängen und eine individuelle, der Zeichenform angepasste Laufweite. Damit fügen sie sich nahtlos und nach typografischen Gesichtspunkten korrekt in den Text ein. Manche Schriften bieten auch Mediävalziffern gleicher Breite für den Tabellensatz an.

Weltweite Verbreitung der europäischen Variante

Von Marokko bis Libyen verwendet man heute anstelle der arabischen die europäische Variante.

Quellen

1. ↑ Die Logik der Lehre von der Leere: Die Shunyata des Nagarjuna: Nagarjuna formuliert die Madhyamika-Lehre.
2. ↑ Robert Kaplan Die Geschichte der Null, Campus Verlag 2000

Weblinks

• http://www.topolewski.de/pascal/jufo2003/entwicklung-der-zahl.htm
• Die arabischen Ziffern, Zahlen und Währungen
• Babylonische Zahlen, ein Einstieg

Zahlensysteme

Ägyptisch | Arabisch | Armenisch | Attisch | Babylonisch | Brahmi | Chinesisch | Etruskische | Glagolitisch | Griechisch | Hebräisch | Indisch | Japanisch | Khmer | Koreanisch | Kyrillisch | Maya | Römisch | Sanskrit | Thai