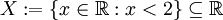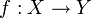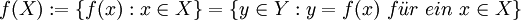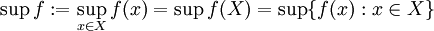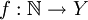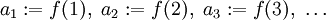- Infimum
-
In der Mathematik treten die Begriffe Supremum, Infimum, obere/untere Schranke, nach oben/unten beschränkt bei der Untersuchung halbgeordneter Mengen auf. Das Konzept der Beschränktheit im Sinn der Existenz von solchen Schranken wird in unterschiedlichen Abwandlungen in fast allen mathematischen Teilgebieten verwendet.
Inhaltsverzeichnis
Definitionen
Suprema (und Infima) von Mengen
Anschauung
Das Supremum (auf deutsch "obere Grenze") einer Menge ist verwandt mit dem Maximum einer Menge und ist – anschaulich gesprochen – ein Element, welches „über“ allen oder „jenseits“ (oberhalb) aller anderen Elementen liegt. Der Ausdruck „über den anderen“ soll andeuten, dass das Supremum nicht das größte Element „unter den anderen“ sein muss, sondern durchaus auch außerhalb („jenseits“) der Menge liegen kann. Und weil es mehrere Elemente geben kann, die dieser Anschauung entsprechen, wird aus Eindeutigkeitsgründen das kleinste Element gewählt, welches diese Eigenschaft hat; sozusagen das Element, das am „nächsten“ oder „unmittelbar“ über allen anderen liegt. (Das Supremum bezeichnet also ein „unmittelbar Darüberliegendes“.) Elemente, die zwar über allen Elementen einer Menge liegen, aber nicht zwingend in unmittelbarer Weise, heißen obere Schranken. Damit ergibt sich dann die Definition des Supremums als kleinste obere Schranke einer Menge.
Das Infimum (deutsch "untere Grenze") einer Menge ist analog definiert, als „unmittelbar Darunterliegendes“ bzw. größte untere Schranke.
Im Reellen
Diese Anschauung lässt sich leicht auf Mengen von reellen Zahlen (als Untermengen der reellen Zahlen) übertragen: Sei
die Menge der reellen Zahlen kleiner als 2. Dann ist 2 das Supremum von X (in
 ). Denn 2 ist eine obere Schranke von X, da sie größer oder gleich (tatsächlich sogar echt größer) allen dessen Elementen ist – also „darüberliegt“. Aber im Gegensatz etwa zu der Zahl 4, die auch eine obere Schranke ist, gibt es keine Zahl kleiner als 2, die auch obere Schranke von X ist. Daher ist 2 kleinste obere Schranke von X, mithin Supremum.
). Denn 2 ist eine obere Schranke von X, da sie größer oder gleich (tatsächlich sogar echt größer) allen dessen Elementen ist – also „darüberliegt“. Aber im Gegensatz etwa zu der Zahl 4, die auch eine obere Schranke ist, gibt es keine Zahl kleiner als 2, die auch obere Schranke von X ist. Daher ist 2 kleinste obere Schranke von X, mithin Supremum.Durch eine kleine Abänderung wird sodann die Verwandtschaft von Supremum und Maximum deutlich. Das Maximum ist nämlich das größte Element „unter allen Elementen“ einer Menge:
Offenbar hat X kein Maximum, da es zu jeder reellen Zahl kleiner als 2 wieder eine reelle Zahl kleiner als 2 gibt, die größer als sie ist. (Der Leser möge sich das veranschaulichen!) Die Zahl 2 ist als Supremum zwar größer als alle Elemente von X, liegt aber nicht in X, da sie nicht echt kleiner als sie selbst ist. Betrachten wir nun die Menge
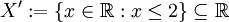 ,
,
so ist 2 Maximum von X', da sie kleiner-gleich als sie selbst ist und es auch keine größere Zahl als 2 gibt, die kleiner-gleich 2 ist. Gleichfalls ist 2 aber auch Supremum von X' wie schon von X, da dieselben Bedingungen wie dort erfüllt sind.
Tatsächlich ist jedes Maximum immer auch Supremum. Daher ist es auch üblich, den Begriff Maximum gar nicht elementar zu definieren, sondern ihn als Sonderfall des Supremums zu benennen, wenn dieses selbst Element der Menge ist, dessen Supremum es darstellt. – Analog gilt das für das Minimum.
Im Allgemeinen
Suprema können jedoch nicht nur auf den reellen Zahlen, sondern allgemein auf halbgeordneten Mengen betrachtet werden. Die formalen Definitionen lauten wie folgt:
Ist M eine halbgeordnete Menge und T eine Teilmenge von M so gilt:
- [Schranke, Beschränktheit]
- Ein Element b ∈ M heißt obere (untere) Schranke von T, wenn gilt:
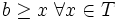 .
.- (Lies: b größer gleich x für alle x aus T)
- Existiert eine obere (untere) Schranke von T, so heißt T nach oben (unten) beschränkt.
- T heißt beschränkt, falls T nach oben und unten beschränkt ist.
- Ist T nicht nach oben (unten) beschränkt, so heißt T nach oben (unten) unbeschränkt.
- T ist unbeschränkt oder nicht-beschränkt, wenn T entweder nach oben oder nach unten oder nach oben und unten unbeschränkt ist.
- (Soll ausgedrückt werden, dass eine Menge sowohl nach oben als auch nach unten unbeschränkt ist, so muss die Menge ausdrücklich als nach oben und unten unbeschränkt beschrieben werden.)
- [Supremum / Infimum]
- Ein Element b ∈ M heißt Supremum von T, wenn b die kleinste obere Schranke von T ist.
- Es heißt Infimum von T, wenn es die größte untere Schranke von T ist.
Ist M die Menge der reellen Zahlen so gilt:
- Ist T nach oben beschränkt, dann besitzt T eine kleinste obere Schranke (Beweisidee unten) und man nennt sie obere Grenze oder Supremum von T – in Zeichen
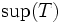 .
. - Ist T nach unten beschränkt, dann besitzt T eine größte untere Schranke (Beweis analog) und man nennt sie untere Grenze oder Infimum von T – in Zeichen
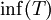 .
. - Falls T nach oben beschränkt und das Supremum von T in T enthalten ist, bezeichnet man das Supremum auch als Maximum von T, in Zeichen max(T).
- Falls T nach unten beschränkt und das Infimum von T in T enthalten ist, bezeichnet man das Infimum auch als Minimum von T, in Zeichen min(T).
- Ist T nach oben unbeschränkt, schreibt man:
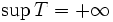 (siehe Unendlichkeit).
(siehe Unendlichkeit).
Das Symbol +∞ ist dabei aber keine reelle Zahl und auch nicht das Supremum von T im hier definierten Sinne: +∞ als Supremumswert ist gerade die formale Schreibweise dafür, dass kein Supremum vorhanden ist. Gelegentlich wird in diesem Zusammenhang +∞ auch als „uneigentliches Supremum“ bezeichnet. - Ist T nach unten unbeschränkt, schreibt man analog:
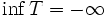 .
.
Suprema (und Infima) von Abbildungen
Abbildungen allgemein
Der Begriff des Supremums auf Mengen wird sinngemäß auch auf Abbildungen (Funktionen) angewendet. Denn das Bild einer Abbildung ist ja immer auch eine Menge. Nämlich für eine Abbildung
die Menge
der sogenannten Elementbilder, d.h. der Bilder der einzelnen Elemente von X unter der Abbildung f.
Ist nun Y eine halbgeordnete Menge, so definiert man
als das Supremum von f auf X – sofern es in Y existiert.
Analog wird das Infimum von f auf X definiert.
Folgen als Abbildungen
Fasst man eine Folge a1, a2, a3, … von Elementen aus Y als Abbildung
auf – also gemäß
– so ergibt sich aus der Definition des Supremums (Infimums) von Abbildungen sofort die Definition des Supremums (Infimums) einer Folge (an) – sofern es in Y existiert.
Eigenschaften
Eindeutigkeit und Existenz
Ist b eine obere Schranke von T und c > b, so ist auch c eine obere Schranke von T. Ist umgekehrt c keine obere Schranke von T und b < c, so ist auch b keine obere Schranke von T. Analoges gilt für untere Schranken.
Das Supremum von T ist (im Falle seiner Existenz) eindeutig bestimmt. Dasselbe gilt für das Infimum von T.
Es ist möglich, dass eine Teilmenge T einer halbgeordneten Menge M mehrere minimale obere Schranken hat, d.h. obere Schranken, so dass jedes kleinere Element keine obere Schranke ist. Sobald T jedoch mehr als eine minimale obere Schranke hat, gibt es keine kleinste obere Schranke, d.h. kein Supremum, von T. Ein Beispiel ist die Menge
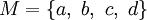 mit der Halbordnung
mit der Halbordnung 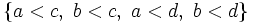 . Hier hat
. Hier hat 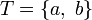 die beiden minimalen oberen Schranken c und d.
die beiden minimalen oberen Schranken c und d.Eigenschaften in Bezug auf eine Epsilon-Umgebung
Sei X eine nichtleere Teilmenge der Reellen Zahlen, dann gilt außerdem für das
- Supremum von X:
-
- Wenn
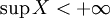 , so existiert für alle ε > 0 ein
, so existiert für alle ε > 0 ein  , so dass
, so dass 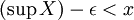 ist.
ist. - Wenn
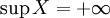 , so existiert für alle k > 0 ein
, so existiert für alle k > 0 ein  , so dass k < x.
, so dass k < x.
- Wenn
- Infimum von X:
-
- Wenn
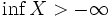 , so existiert für alle ε > 0 ein
, so existiert für alle ε > 0 ein  , so dass
, so dass 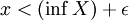 ist.
ist. - Wenn
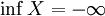 , so existiert für alle k > 0 ein
, so existiert für alle k > 0 ein  , so dass x < − k.
, so dass x < − k.
- Wenn
Existenz des Supremums für beschränkte Teilmengen der reellen Zahlen
Die Existenz des Supremums für eine beschränkte Teilmenge M der reellen Zahlen kann auf mehrere Arten gezeigt werden:
Zum einen kann man die Existenz von Supremum und Infimum für beschränkte Teilmengen der reellen Zahlen einfach als Axiom festlegen. Diese Forderung wird oft Supremumsaxiom oder Vollständigkeitsaxiom genannt.
Geht man von dem Axiom aus, dass jede Intervallschachtelung genau eine reelle Zahl definiert, kann man wie folgt vorgehen: Man konstruiert eine Intervallschachtelung, die das Supremum einschließt. Dazu konstruiert man zwei Folgen, von denen die erste (an) monoton wachsend ist und nicht aus oberen Schranken von M besteht, die zweite (bn) monoton fallend ist und aus oberen Schranken von M besteht, so dass noch gilt, dass die Abstände entsprechender Folgeglieder gegen 0 gehen (indem man jeweils die Intervallmitte betrachtet und entscheidet, ob sie eine obere Schranke ist oder nicht). Damit erhält man den gemeinsamen Grenzwert sup(M) der beiden Folgen als kleinste obere Schranke von M, denn:
Jedes Element von M ist kleiner-gleich jedem Element bn der oberen Folge, also kleiner-gleich sup(M), deshalb ist sup(M) eine obere Schranke von M. Und jede reelle Zahl, die kleiner ist als sup(M), ist kleiner als wenigstens ein Element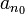 (für ein gewisses n0) der unteren Folge, also keine obere Schranke.
(für ein gewisses n0) der unteren Folge, also keine obere Schranke.Eine äquivalente Formulierung zur Existenz des Supremums ist das Schnittaxiom, nachdem jeder Dedekindsche Schnitt von einer reellen Zahl erzeugt wird.
Im Bereich der hyperkomplexen Zahlen kommt es bisweilen vor, dass Suprema gleichzeitig sowohl Maxima als auch keines sein können. Dieser Sachverhalt bildet einen Teil der Quantenmechanik ab, insbesondere den der hochenergetischen Teilchen.
Beispiele
Reelle Zahlen
Folgende Beispiele beziehen sich auf Teilmengen der reellen Zahlen.
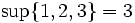
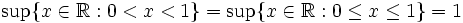
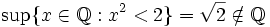
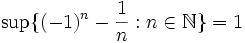
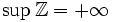
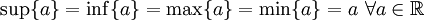
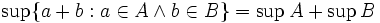
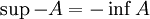 bzw.
bzw. 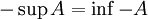 , wobei
, wobei 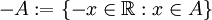
Andere halbgeordnete Mengen
Auf
 hat jede beschränkte Teilmenge ein Supremum bzw. Infimum. Betrachtet man andere Mengen, auf denen Ordnungsrelationen definiert sind, so ist dies nicht zwingend:
hat jede beschränkte Teilmenge ein Supremum bzw. Infimum. Betrachtet man andere Mengen, auf denen Ordnungsrelationen definiert sind, so ist dies nicht zwingend:- Die Menge
 der rationalen Zahlen ist bezüglich der natürlichen Ordnung total geordnet. Die Menge
der rationalen Zahlen ist bezüglich der natürlichen Ordnung total geordnet. Die Menge 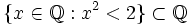 ist beispielsweise durch die Zahl
ist beispielsweise durch die Zahl 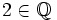 nach oben beschränkt, hat aber kein Supremum in
nach oben beschränkt, hat aber kein Supremum in  .
. - In der bezüglich Inklusion partiell geordneten Menge
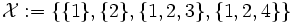 ist die Menge
ist die Menge 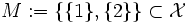 sowohl durch das Element
sowohl durch das Element 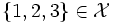 als auch durch
als auch durch 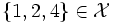 nach oben beschränkt. Ein Supremum, also eine kleinste obere Schranke von
nach oben beschränkt. Ein Supremum, also eine kleinste obere Schranke von 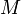 , existiert in
, existiert in 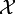 jedoch nicht.
jedoch nicht.
Siehe auch
- Aus dem Begriff Supremum wird in der Maßtheorie der Begriff des wesentlichen Supremums abgeleitet, der zum Beispiel in der Theorie der Lp-Räume eine wichtige Rolle spielt.
- Die Untersuchung von partiell geordneten Mengen, in denen zu jeder zweielementigen Teilmenge ein Supremum und ein Infimum existiert, ist Gegenstand der Verbandstheorie.
Literatur
- Stefan Hildebrandt: Analysis 1. Springer 2005, ISBN 3-540-25368-8.
Wikimedia Foundation.