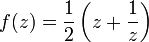Joukowski-Transformation

Urbild und Bild einer Kutta-Schukowski-Transformation

Die Kutta-Schukowski-Transformation, oft auch nur Schukowski-Transformation oder nach anderer Transkription Joukowski-Transformation genannt, ist ein mathematisches Verfahren, das Anwendung in der Strömungslehre und Elektrostatik findet. Sie ist die einfachste Transformation, die auf einen Kreis angewendet als Ergebnis Tragflächenprofile liefert. Sie ist nach Martin Wilhelm Kutta und Nikolai Jegorowitsch Schukowski benannt.

Definition

Die Kutta-Schukowski-Transformation lässt sich mit komplexen Zahlen darstellen, es handelt sich um eine konforme Abbildung. Sie entspricht also einer Funktion 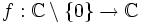$f: \mathbb{C}\setminus\{0\} \rightarrow \mathbb{C}$ mit der Gleichung

$f(z) = \frac{1}{2} \left(z+\frac{1}{z}\right)$

Anwendung

Um Tragflächenkonturen mit gewölbter Mittellinie zu erzeugen, sind zudem noch geometrische Berechnungen nötig, da hier der Ausgangspunkt der Transformation nicht das Zentrum, sondern ein um x und y verschobener Punkt innerhalb des Kreises sein muss. Der immense Vorteil des Verfahrens von Kutta und Schukowski besteht darin, dass man sich damit in der Lage befindet, aus deren Ergebnis zusätzlich Auftrieb sowie Geschwindigkeits,- und Druckverteilung um eine derartige Tragfläche unmittelbar zu errechnen, wodurch die experimentelle Seite der Tragflächenforschung um die mathematische Seite hin ergänzt und daher ein Vergleich zwischen Theorie und Experiment erst möglich gemacht wird.

Anschaulich kann mit Hilfe dieser Transformation ein Tragflächenprofil auf eine einfache Zylindergeometrie zurückgeführt werden, welche relativ leicht exakt berechnet werden kann.

Allerdings haben derartig berechnete Profile auch gravierende Nachteile, wie Strömungsablösung und erhöhte Wirbelbildung, weshalb in der Praxis kompliziertere Transformationsgleichungen benützt werden, welche bessere Profile ergeben.

Geschichte

Kutta benutzte die Transformation für Tragflächenprofile, welche aus unendlich dünnen Kreisbogensegmenten bestanden. Schukowski zeigte, dass man mit dieser Methode auch Profile endlicher Dicke sowie gekrümmter Mittenkontur berechnen kann.

Weblinks

• Geometrische Grundlagen