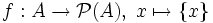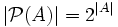Kardinalität (Mathematik)

In der Mathematik verwendet man den aus der Mengenlehre von Cantor stammenden Begriff der Mächtigkeit oder Kardinalität, um den für endliche Mengen verwendeten Begriff der „Anzahl der Elemente einer Menge“ auf unendliche Mengen zu verallgemeinern.

Für endliche Mengen setzt man die Mächtigkeit gleich der Anzahl der Elemente der Menge, das ist eine natürliche Zahl (oder die Null). Für unendliche Mengen benötigt man etwas Vorarbeit, um ihre Mächtigkeiten zu charakterisieren. Die im folgenden gemachten Definitionen und Folgerungen sind aber auch im Falle endlicher Mengen gültig.

Mächtigkeit bei endlichen Mengen

Bei einer endlichen Menge X bezeichnet die Mächtigkeit die Anzahl der Elemente von X, geschrieben als | X | .

Beispiele:

A = {1, 3, 7, 21} => | A | = 4

B = {Tetraeder, Hexaeder, Oktaeder, Dodekaeder, Ikosaeder} => | B | = 5

C = {rot, grün, blau, gelb, magenta, cyan} => | C | = 6

Die Potenzmenge 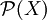$\mathcal P(X)$ einer endlichen Menge X hat genau 2 ^{| X |} Elemente: die Wahl einer Teilmenge entspricht den | X | unabhängigen Wahlen zwischen den zwei Möglichkeiten, ob ein bestimmtes Element von X in der Teilmenge liegen soll oder nicht.

Gleichmächtigkeit, Mächtigkeit

Man definiert zunächst den Begriff der Gleichmächtigkeit zweier beliebiger Mengen A und B:

Eine Menge A heißt gleichmächtig zu einer Menge B, wenn es eine Bijektion 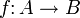$f\colon A \to B$ gibt. Man schreibt dann | A | = | B | .

Ist A gleichmächtig zu B und f eine Bijektion zwischen A und B, dann ist auch die Umkehrfunktion von f eine Bijektion, also ist auch B gleichmächtig zu A. Endliche Mengen sind genau dann gleichmächtig, wenn sie gleich viele Elemente haben. Unendliche Mengen sind Mengen, die zu sich gleichmächtige echte Teilmengen besitzen.

Man nennt eine Menge, die gleichmächtig zur unendlichen Menge 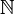$\Bbb N$ der natürlichen Zahlen ist, eine abzählbare Menge.

Eine Menge A, die höchstens gleichmächtig zu 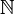$\Bbb N$ ist, heißt höchstens abzählbar. Oft jedoch wird abzählbar als höchstens abzählbar definiert, während eine Menge, die gleichmächtig zu 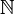$\Bbb N$ ist, abzählbar unendlich genannt wird. Dies macht die Formulierung vieler Beweise etwas einfacher. Wir wollen jedoch im Rahmen dieses Artikels die oben zuerst eingeführte Definition von abzählbar verwenden.

Besondere Ergebnisse:

1. Gleichmächtig sind: 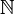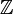$\Bbb N$, $\Bbb Z$ und $\Bbb Q$ (also die Mengen der natürlichen, der ganzen und der rationalen Zahlen).

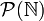2. Gleichmächtig sind: $\Bbb R$, $\left]0,1\right[$, C und $\mathcal P(\Bbb N)$, wobei C die Cantor-Menge ist.

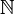3. Die Menge $\Bbb R$ der reellen Zahlen ist mächtiger als $\Bbb N$ (also überabzählbar)

Siehe auch: Cantor-Diagonalisierung, Cantors zweites Diagonalargument

Kardinalzahlen

Da man leicht zeigen kann, dass die Gleichmächtigkeit von Mengen eine Äquivalenzrelation ist, ergibt die folgende Definition einen Sinn:

Die Äquivalenzklassen der Mengen bezüglich der Relation der Gleichmächtigkeit nennt man Kardinalzahlen.

Aleph ($\aleph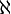$) ist der erste Buchstabe des hebräischen Alphabets, er wird mit einem Index verwendet, um Kardinalzahlen unendlicher Mengen zu benennen.

Liegt eine Menge A in der Äquivalenzklasse (= Kardinalzahl) 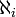$\aleph_i$, dann sagt man, A hat die Mächtigkeit 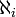$\aleph_i$. Man schreibt dann:

$|A| = \aleph_i$.

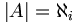Die Kardinalzahl einer endlichen Menge mit n Elementen wird mit der natürlichen Zahl n gleichgesetzt.

Man kann sich nun fragen, ob alle unendlichen Mengen einander gleichmächtig sind – in dem Fall wären alle unendlichen Mengen abzählbar.

Es stellt sich jedoch heraus, dass es unendliche Mengen gibt, die nicht gleichmächtig zueinander sind, z. B. ist die Menge der natürlichen Zahlen nicht gleichmächtig zur Menge der reellen Zahlen. Das kann man z. B. mit dem so genannten „Cantorschen Diagonalbeweis“ zeigen, siehe dazu den Artikel überabzählbar.

Weiter unten wird gezeigt, dass es unendlich viele verschiedene Kardinalzahlen gibt.

Indem man zeigt, dass jede Menge gleichmächtig zu einer wohlgeordneten Menge ist (dies ist die Aussage des Wohlordnungssatzes), kann man jede Kardinalzahl mit der kleinsten ihr gleichmächtigen Ordinalzahl gleichsetzen.

Vergleich der Mächtigkeit

Um die Mächtigkeiten ungleichmächtiger Mengen vergleichen zu können, legt man fest, wann eine Menge B mächtiger als eine Menge A sein soll:

• Wenn es eine Bijektion f von A auf eine Teilmenge von B gibt, dann heißt A höchstens gleichmächtig zu B. Man schreibt dann |A| ≤ |B|.

• Wenn es eine Bijektion f von A auf eine Teilmenge von B gibt, aber keine Bijektion von A nach B existiert, dann heißt A weniger mächtig als B und B mächtiger als A. Man schreibt dann |A| < |B|. Offenbar gilt |A| < |B| genau dann, wenn |A| ≤ |B| aber nicht |A| = |B| ist.

Nun stellt sich aber die delikate Frage nach der Vergleichbarkeit zweier beliebiger Mengen, ob also die bloße Eigenschaft, eine Menge zu sein, eine solche Vergleichsmöglichkeit impliziert. Und tatsächlich kann man für zwei beliebige Mengen im Allgemeinen zeigen:

• A, B Mengen ⇒ |A| ≤ |B| ∨ |B| ≤ |A| (Vergleichbarkeitssatz).

Des Weiteren kann man zeigen, dass jede Menge, die höchstens abzählbar ist, entweder endlich oder gleichmächtig zu 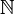$\Bbb N$ ist. Außerdem kann man zeigen, dass jede unendliche Menge eine zu 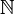$\Bbb N$ gleichmächtige Teilmenge enthält.

Damit ist die Mächtigkeit von 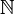$\Bbb N$ die kleinste unendliche Kardinalzahl. Man bezeichnet sie mit $\aleph_0$:

$\aleph_0 := |\Bbb N|$.

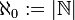Die Kontinuumhypothese (CH) besagt, dass es keine Menge gibt, die mächtiger ist als 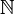$\Bbb N$, aber weniger mächtig als $\R$ . Wie der Name jedoch schon vermuten lässt, ist dies kein Satz in dem Sinne, dass er sich beweisen lässt. Weder die Kontinuumhypothese noch ihre Verneinung lässt sich aus den üblichen Axiomensystemen herleiten (z. B. der Zermelo-Fraenkel-Mengenlehre mit Auswahlaxiom).

Die Kontinuumhypothese besagt also, dass 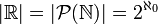$|\Bbb R| = |\mathcal P(\Bbb N)| = 2^{\aleph_0}$ die zweitkleinste unendliche Kardinalzahl 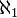$\aleph_1$ ist.

Totale Ordnung der Mächtigkeiten

Bei naiver Betrachtung der Schreibweise könnte man vermuten, dass für Mengen A und B mit |A| ≤ |B| und |B| ≤ |A| stets |A| = |B| gilt. Dass das tatsächlich so ist, wird vom folgenden Satz ausgesagt:

Cantor-Bernstein-Schröder-Theorem: Ist A höchstens gleichmächtig zu B und B höchstens gleichmächtig zu A, dann sind A und B gleichmächtig.

Fassen wir einige Eigenschaften der Mächtigkeiten zusammen:

• Es gilt stets |A| = |A| (nimm die Identität als Bijektion).
• Aus |A| ≤ |B| und |B| ≤ |A| folgt |A|=|B|.
• Aus |A| ≤ |B| und |B| ≤ |C| folgt |A| ≤ |C| (folgt sofort aus der Definition).
• Für zwei Mengen A und B gilt stets |A| ≤ |B| oder |B| ≤ |A| (das ist äquivalent zum Auswahlaxiom).

Damit ist gezeigt, dass die Kardinalzahlen total geordnet sind.

Rechenregeln zur Kardinalität

Der Basissatz ist ein nützliches Hilfsmittel der Mengenlehre zur Berechnung von Mächtigkeiten und Kardinalzahlen

Basissatz

Es seien M,N sowie 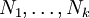$N_1, \ldots, N_k$ endliche Mengen. Dann besagt der Satz

Bijektions- oder Isomorphieregel

M ist bijektiv auf N abbildbar 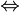$\Leftrightarrow$ | M | = | N | .

Summenregel

$M \cap N = \emptyset \Leftrightarrow |M \cup N| = |M| + |N|$

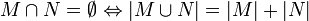
Differenzenregel

$M \subseteq N \Leftrightarrow |N \setminus M| = |N| - |M|$

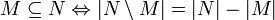
Produktregel

$|M \times N| = |M| \cdot |N|$

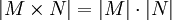
Quotientenregel

Ist 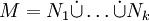$M = N_1 \dot\cup \ldots \dot\cup N_k$ und gilt 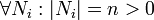$\forall N_i : |N_i| = n &amp;gt; 0$, so folgt 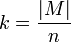$k = \frac{|M|}{n}$ bzw. $|M| = k \cdot n$

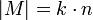
Subadditivität von Mengen

Seien S_i Mengen, so gilt

$\Big|\bigcup_i S_i\Big| \leq \sum_{i}|S_i|$.

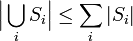Falls die S_i paarweise disjunkt sind, so gilt die Gleichheit: $|\bigcup_i S_i| = \sum_{i}|S_i|$.

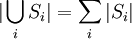Das heißt also, dass bei disjunkten Mengen die Anzahl der Elemente in der Vereinigung der Mengen S_i gleich der Summe der einzelnen Anzahlen von Elementen in jeder dieser Mengen ist.

Beispiele

M = {1,2,3} und N = {1,3,5,7}. Dann

• existiert keine bijektive Abbildung zwischen M und N,
• ist $|M \cup N| = |\{1,2,3,5,7\}| = 5$,
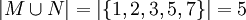• lässt sich die Differenz nicht mit obigem Satz bestimmen
• beträgt das kartesische Produkt $|M| \cdot |N| = |\{(1,1); (1,3); \ldots\}| = 12$.

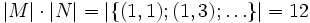In einem weiteren Beispiel sei M = {1,2,3,4} und N₁ = {1},N₂ = {2},N₃ = {3},N₄ = {4},N = {1,2,3,4}. Dann

• existieren bijektive Abbildungen (identische Abbildung) zwischen den beiden Mengen M und N,
• ist 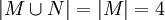$|M \cup N| = |M| = 4$, da die beiden Mengen identisch sind,
• ist M ein Teilmenge von N und somit deren Differenz definiert. Sie beträgt $\emptyset$.
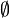• Das kartesische Produkt beträgt 16 und
• da 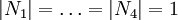$|N_1| = \ldots = |N_4| = 1$ erhalten wir k = 1 bzw.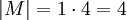 $|M| = 1 \cdot 4 = 4$

Mächtigkeit der Potenzmenge, Größte Mächtigkeit

Die Frage nach der größten Mächtigkeit einer Menge beantwortet der folgende Satz (Satz von Cantor):

Für jede Menge A ist die Potenzmenge P(A) mächtiger als A.

Beweis: Dass |A| ≤ |P(A)| gilt, sieht man, indem man A bijektiv auf die einelementigen Teilmengen von P(A) abbildet:

$f:A\to\mathcal{P}(A),\; x\mapsto\{x\}$

Diese Funktion f ist offenbar injektiv und es gilt demnach, dass |A| ≤ |P(A)| ist (*).

Der Beweis, dass keine Bijektion von A nach P(A) existiert, ist etwas trickreicher. Man betrachtet für eine widerspruchshalber angenommene Bijektion g: A → P(A) die Menge

$M:=\{x \in A \mid x \not\in g(x)\} \in \mathcal{P}(A)$.

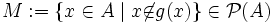g ist also eine Funktion, die Elemente von einer Menge A auf Teilmengen von A, also Elemente der Potenzmenge P(A) abbildet. Und M ist eine Teilmenge von A, also auch ein Element der Potenzmenge P(A). Da g als bijektiv vorausgesetzt ist, also g insbesondere surjektiv ist, muss es ein x in A geben mit g(x) = M. Läge nun x in M, dann wäre nach Definition von M x nicht in g(x) = M. Läge x dagegen nicht in M, dann wäre x in g(x) = M, wieder nach der Definition von M. Damit haben wir einen Widerspruch erhalten, der zeigt, dass die angenommene Bijektion g nicht existieren kann. Dies zeigt, dass es überhaupt keine bijektive Abbildung von A in P(A) geben kann. Daher gilt, dass |A| ungleich |P(A)| ist. Zusammen mit (*) gilt also: |A| < |P(A)|.

Für die Mächtigkeit von P(A) gibt es auch folgende Schreibweise:

$|\mathcal{P}(A)| = 2^{|A|}$

Beachte aber, dass der entsprechende Ausdruck für unendliche Ordinalzahlen einen ganz anderen Wert liefert, und z. B. 2^|N| nicht als ein „Grenzwert“ einer Folge (2ⁿ) angesehen werden kann.

Bestimmt man nun die Mächtigkeiten der Potenzmengen von Potenzmengen von Potenzmengen usw., dann sieht man, dass es unendlich viele Kardinalzahlen gibt, und keine mächtigste Menge existiert.

Literatur

• Erich Kamke: Mengenlehre. de Gruyter, Berlin und Leipzig 1928 (Sammlung Göschen, No. 999, 159 Seiten).  – Eine gute Einführung in die Mengenlehre.