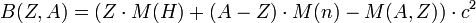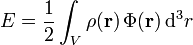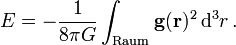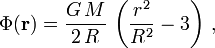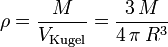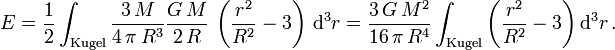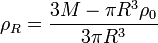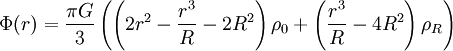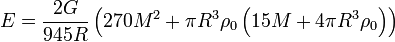Kernbindungsenergie

Bindungsenergie wird freigesetzt, wenn zwei oder mehr Bestandteile durch Anziehungskräfte zusammengebracht werden und miteinander ein gebundenes System (beispielsweise einen Himmelskörper, ein Molekül, ein Atom, einen Atomkern) bilden. Diese Freisetzung bedeutet, dass das gebundene System eine negative potentielle Energie hat. Um die Bestandteile wieder zu trennen, muss eine gleich große Arbeit von außen geleistet, also dem System wieder zugeführt werden, um die bindenden Kräfte zu überwinden.

Die Bezeichnung Bindungsenergie ist ein gängiger Fachausdruck, aber sprachlich etwas unglücklich gewählt. Sie führt – besonders mit einem nachfolgenden Genitiv, wie z. B. Bindungsenergie „des Uran-Atomkerns“ – leicht zu dem Missverständnis, es handele sich um einen (positiven) Energiebetrag, der in dem gebundenen System vorhanden ist und aus ihm freigesetzt werden kann. Richtig ist, wie oben gesagt, das Gegenteil: die Bindungsenergie ist bereits bei der Bildung des gebundenen Systems freigesetzt und abgegeben worden, ist also gerade nicht mehr verfügbar.

Chemische Bindungsenergie

Die Bindungsenergie ist das Maß für die Stärke einer Bindung. Sie wird auch Dissoziationsenthalpie genannt, wenn sie zum Trennen (Dissoziation) der verbundenen Atome aufgewendet werden muss. Angegeben wird sie in Elektronvolt pro Atom oder Molekül oder auch in Kilojoule pro Mol.

• Die größte Bindungsenergie überhaupt weist Aluminiumoxid mit 157 eV auf.
• Sehr große Bindungsenergien beobachtet man bei Ionenkristallen wie Magnesiumsulfid oder Kochsalz mit Werten zwischen 8 und 35 eV.
• Bindungsenergien zwischen Atomen betragen bei Molekülen, die bei Zimmertemperatur stabil sind, meist zwischen 3 und 7 eV pro Bindung. Eine Trennung ist hier beispielsweise durch Hitze oder energiereiche Photonen möglich.
• Besonders geringe Bindungsenergie beobachtet man bei Wasserstoffbrückenbindungen. Sie sind mit nur 17 kJ/mol bis 167 kJ/mol^[1] oder 0,18 eV bis 1,7 eV deutlich schwächer als die Bindungskraft innerhalb eines Moleküls. Diese Bindungen sind wegen der ständigen Bewegung der Atome bei Zimmertemperatur instabil. Deshalb bleibt die Wasserstoffbrücke im Wasser nur Bruchteile einer Sekunde bestehen. Dann lösen sich die Moleküle voneinander, um erneut eine Wasserstoffbrückenbindung mit einem anderen Molekül einzugehen. Andererseits hält die Wasserstoffbrückenbindung die beiden Stränge in der DNA sehr fest zusammen, weil es längs des langgestreckten Moleküls sehr viele gibt und immer ein genügend hoher Anteil davon gebunden ist. Die gerade nicht gebundenen können ihren Platz nicht verlassen, so dass ihre erneute Bindung wieder mit ihrem vorigen Partner erfolgt.
• Die noch schwächeren Van-der-Waals-Kräfte beispielsweise zwischen ungeladenen Edelgasatomen zählen Chemiker nicht mehr zu den „Bindungen“, weil sie mit derart geringen Energien zwischen 0,005 und 0,050 eV getrennt werden können, dass die entsprechenden Moleküle bei Zimmertemperatur instabil sind. Vergleichbares gilt für Disulfidbrücken.

In der quantenmechanischen Beschreibung kommt die Bindungsenergie dadurch zustande, dass bei Annäherung zweier Atome die jeweiligen Valenzorbitale einen bindenden und einen antibindenden Zustand erzeugen. Der bindende Zustand liegt energetisch unterhalb der einzelnen Valenzzustände. Wenn die Valenzzustände jeweils nur ein Elektron besitzen, werden deren Energieeigenwerte herabgesetzt. Die bei der Überlappung freiwerdende Energie ist die Bindungsenergie.

Atomphysik

In der Atomphysik wird als Bindungsenergie die Energie bezeichnet, die beim Einfangen eines Elektrons in die Elektronenhülle freigesetzt wird. Sie kommt durch die elektrische Anziehung zwischen Elektron und Atomkern zustande. Um wieder die einzelnen Teile zu erhalten, also das Elektron aus dem Atom zu entfernen, muss man einen gleich großen Energiebetrag zuführen. Manchmal ist mit Bindungsenergie diejenige des gesamten Atoms (also nicht nur eines einzelnen Elektrons) gemeint.

Beim Wasserstoffatom beträgt die Bindungsenergie 13,6 eV, beim Cäsiumatom für das "äußerste" Elektron nur 3,9 eV.

Um ein Elektron aus einem ungeladenen Festkörper zu entfernen, muss Energie aufgewendet werden, die als Austrittsarbeit bezeichnet wird. Sie ist oft erheblich geringer als die Bindungsenergie im isolierten Atom und beträgt z. B. beim Cäsium nur 2,14 eV. Ihr Wert lässt sich durch den Schottky-Effekt verringern. Die Austrittsarbeit ist z. B. beim Edison-Richardson-Effekt, Sekundärelektronenvervielfacher, Sekundärelektronenmikroskop und photoelektrischen Effekt von Bedeutung.

Auch bei einem Metall-Halbleiter-Übergang wie in der Schottky-Diode müssen Elektronen die Schottky-Barriere überwinden, diese liegt meist zwischen 0,5 und 0,9 eV. Die Bandlücke im Bändermodell eines Halbleiters entspricht der Bindungsenergie eines Elektrons im Valenzband.

Kernphysik

In der Kernphysik ist die Bindungsenergie die Energiemenge, die frei wird, wenn sich Nukleonen zu einem Atomkern verbinden. Dies ist nach der einsteinschen Beziehung E = mc² mit einem kleinen Massenverlust der gebundenen Nukleonen verbunden, dem Massendefekt.

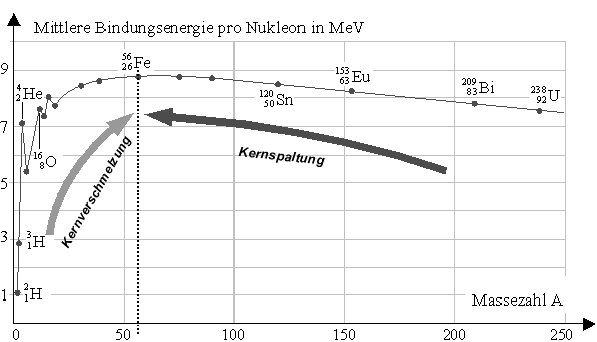
Bindung kommt durch die anziehende Kraft der starken Wechselwirkung zwischen den Nukleonen zustande. Sie wird durch die gegenseitige Coulomb-Abstoßung der elektrisch positiv geladenen Protonen im Kern geschwächt. Die maximale Bindungsenergie pro Nukleon ist ungefähr bei Eisen erreicht und nimmt zu schwereren Nukliden hin wieder ab: Je mehr Protonen vorhanden sind, desto größer ist die abstoßende Coulombkraft zwischen ihnen. Daher kann im Gebiet der leichten Kerne durch Kernverschmelzung (Kernfusion), im Gebiet der schweren Kerne durch Kernspaltung Nutzenergie gewonnen werden, wie in der Abbildung angedeutet ist.

Die Zacken in der Graphik hängen mit den Magischen Zahlen zusammen.

Siehe auch: Bethe-Weizsäcker-Formel

Kernbindungsenergie in Abhängigkeit von der Kernmasse

Die Bindungsenergie B definiert man üblicherweise aus der Masse der Atome, weil diese wesentlich präziser gemessen werden kann als die Masse der Kerne:

$B(Z,A) = \left(Z \cdot M(H) + (A - Z) \cdot M(n) - M(A,Z)\right) \cdot c^2$

Hierbei ist M(H) die Masse des H-Atoms, M(n) die Masse des Neutrons, M(A,Z) die Masse des Atoms mit Z Elektronen und einem Kern mit A Nukleonen (A die Massenzahl und Z die Ordnungszahl).

Gravitation

Die gravitative Bindungsenergie ist diejenige Energie, die benötigt wird, um einen durch Gravitation zusammengehaltenen Körper (z. B. die Erde) in sehr viele winzige Bestandteile zu zerlegen und diese unendlich weit voneinander zu entfernen. Die gleiche Energie wird freigesetzt, wenn sich eben diese Bestandteile zu einem gravitativ gebundenen Körper zusammenfügen.

In Newtons Gravitationstheorie ist die potentielle Energie einer Massendichte 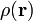$\rho(\mathbf r)$ das Volumenintegral

$E=\frac{1}{2}\int_V \rho(\mathbf r)\, \Phi(\mathbf r)\,\mathrm d^3 r$

oder äquivalent

$E=-\frac{1}{8 \pi G}\int_{\text{Raum}} \mathbf g(\mathbf r)^2 \,\mathrm d^3r\,.$

Dabei ist 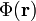$\Phi(\mathbf r)$ das Gravitationspotential der Massendichte und 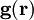$\mathbf g (\mathbf r)$ die Gravitationsbeschleunigung. Es ist zu beachten, dass in der ersten Formel nur über das Volumen der Massenverteilung, in der zweiten Formel jedoch über den gesamten Raum integriert wird.

Beispielsweise ergibt sich für das Potential im Inneren einer homogenen Kugel, also einer Kugel mit konstanter Dichte (Herleitung)

$\Phi(\mathbf r) = \frac{G\,M}{2\,R}\,\left(\frac{r^2}{R^2}-3\right)\,,$

wobei M die Masse des Körpers, R der Radius und G die Gravitationskonstante ist. Zusammen mit der Dichte

$\rho = \frac{M}{V_{\text{Kugel}}}= \frac{3\, M}{4\, \pi\, R^3}$

führt dies zur Bindungsenergie

$E = \frac{1}{2}\int_{\text{Kugel}} \frac{3\, M}{4\, \pi\, R^3} \frac{G\,M}{2\,R}\,\left(\frac{r^2}{R^2}-3\right)\, \mathrm d^3 r = \frac{3\, G\, M^2}{16\, \pi\, R^4}\int_{\text{Kugel}}\left(\frac{r^2}{R^2}-3\right) \mathrm d^3 r\,.$

Da über eine Kugel integriert werden muss, ist es am einfachsten, dies in Kugelkoordinaten zu tun. Das Volumenelement d³r hat in diesen Koordinaten die Gestalt

$\, \mathrm{d}^3 r=r^2\, \sin \theta \, \mathrm{d}\varphi \, \mathrm{d}\theta \, \mathrm{d}r$,

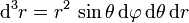wobei $\varphi$ der Azimutwinkel und θ der Polarwinkel ist. Damit wird das Integral zu

$E = \frac{3\, G\, M^2}{16\, \pi\, R^4}\int_0^R \int_0^\pi\int_0^{2\pi} \left(\frac{r^2}{R^2}-3\right)\, r^2\, \sin \theta \, \mathrm{d}\varphi \, \mathrm{d}\theta \, \mathrm{d}r$.

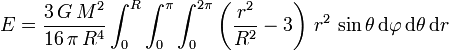Für die beiden Integrale über die Winkel ergibt sich einfach

$\int_0^\pi\int_0^{2\pi} \sin \theta \, \mathrm{d}\varphi \, \mathrm{d}\theta = 4\, \pi$,

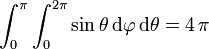also die potentielle Energie

$E = \frac{3\, G\, M^2}{4\, R^4}\int_0^R \left(\frac{r^4}{R^2}-3 r^2\right)\, \mathrm{d}r = \frac{3\, G\, M^2}{4\, R^4}\left(\frac{R^5}{5 R^2}-\frac{3 R^3}{3}\right) = -\frac{3\, G\, M^2}{5\, R}$.

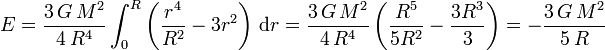Die Bindungsenergie beträgt also

$E = \frac{3\, G\, M^2}{5\, R}$.

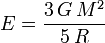Eine homogene Kugel mit Masse und Radius der Erde besäße nach dieser Formel eine gravitative Bindungsenergie von etwa 2,24 · 10³² J.

Näherung für reale Himmelskörper

Aufgrund der Eigenkompression ist die Dichte eines realen Himmelskörpers in seinem Kern höher als nahe der Oberfläche. Daher übersteigt seine gravitative Bindungsenergie die einer homogenen Kugel gleicher Masse und Größe. Sie lässt sich näherungsweise unter der Annahme berechnen, dass die Dichte mit steigendem Radius linear abnimmt:

$\rho(r)=\left(\rho_0-\rho_R\right)\cdot\left(1-\frac{r}{R}\right)+\rho_R$,

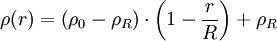wobei ρ₀ die Kerndichte des Himmelskörpers und ρ_R seine Oberflächendichte ist. Da dies natürlich dennoch eine Idealisierung ist, können wir nur für die Kerndichte den realen Wert benutzen. Die Oberflächendichte müssen wir hingegen so wählen, dass sich die bekannte Masse des betrachteten Himmelskörpers ergibt.

Die Masse einer Kugel mit linear abnehmender Dichte beträgt

$M=\pi R^3\left(\frac{\rho _0}{3}+\rho _R\right)$,

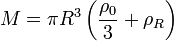womit wir für die passende Oberflächendichte

$\rho _R = \frac{3 M-\pi R^3 \rho _0}{3 \pi R^3}$

erhalten. Das Potential im Innern der Kugel ergibt sich durch Lösen der Poisson-Gleichung zu

$\Phi(r)=\frac{\pi G}{3}\left(\left(2 r^2-\frac{r^3 }{R}-2 R^2\right)\rho _0+\left(\frac{r^3 }{R}-4 R^2\right)\rho _R\right)$

Mit diesen Größen und den Formeln aus dem letzten Abschnitt kann nun die Bindungsenergie berechnet werden. Sie beträgt

$E=\frac{2 G }{945 R}\left(270 M^2+\pi R^3 \rho _0 \left(15 M+4 \pi R^3 \rho _0\right)\right)$

Für die Erde ist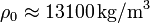 $\rho _0 \approx 13100 \, \mathrm{kg/m^3}$. Ihre Bindungsenergie beträgt demnach etwa 2,45 · 10³² J

Weblinks

• Was ist Bindungsenergie?, Flash-Video aus der Fernsehsendung alpha-Centauri (JavaScript benötigt)

Einzelnachweise

1. ↑ George A. Jeffrey: An Introduction to Hydrogen Bonding. Oxford University Press, 1997, ISBN 978-0195095494.