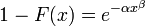- Kohlrausch-Funktion
-
Die Weibull-Verteilung ist eine statistische Verteilung, die beispielsweise zur Untersuchung von Lebensdauern in der Qualitätssicherung verwendet wird. Man verwendet sie vor allem bei Fragestellungen wie Materialermüdungen von spröden Werkstoffen oder Ausfällen von elektronischen Bauteilen, ebenso bei statistischen Untersuchungen von Windgeschwindigkeiten. Benannt ist sie nach dem Schweden Waloddi Weibull (1887-1979).
Ein anschauliches Beispiel für die Anwendung der Weibull-Statistik ist die Ausfallwahrscheinlichkeit einer Kette. Das Versagen eines Glieds führt zum Festigkeitsverlust der ganzen Kette. Spröde Werkstoffe zeigen ein ähnliches Bruchverhalten. Es genügt ein Riss, der die kritische Risslänge überschreitet, um das Bauteil zu zerstören.
So erklärt sich auch die Abhängigkeit der Festigkeit spröder Werkstoffe von der Geometrie. Das Verlängern einer Kette (bzw. eines spröden Bauteils) reduziert die Festigkeit, eine Verstärkung der Kettenglieder (bzw. Vergrößerung des Bauteil-Querschnitts) erhöht sie.
Die Weibull-Verteilung kann zur Beschreibung steigender, konstanter und fallender Ausfallraten technischer Systeme verwendet werden.
In der Praxis ist die Weibull-Verteilung neben der Exponentialverteilung die am häufigsten verwendete Lebensdauerverteilung.
Inhaltsverzeichnis
Definition
Die Dichtefunktion der Weibull-Verteilung
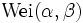 ist
istund ihre Verteilungsfunktion lautet
für x > 0, α > 0 und β > 0.
Die Grafik zeigt die Dichtefunktionen der Weibull-Verteilung für verschiedene Werte von β. Man sieht, dass der Fall β = 1 die Exponentialverteilung ergibt. β < = 1 ergibt eine streng monoton fallende Sterberate.
Für β = 3,4 ergäbe sich eine Verteilung ähnlich der Normalverteilung.
Verbreitete Darstellung
Die Verteilungsdichte lautet hierbei
mit der Verteilungsfunktion
für t > 0, T > 0 und b > 0. Dabei ist t die Zeit (oder Festigkeit, ...), T die charakteristische Lebensdauer (d.h. Lebensdauer bei einer Ausfallwahrscheinlichkeit von 63,2 %, Festigkeitsniveau bei einer Ausfallwahrscheinlichkeit von 63,2 %, ...) und b der sog. Weibull-Modul m.
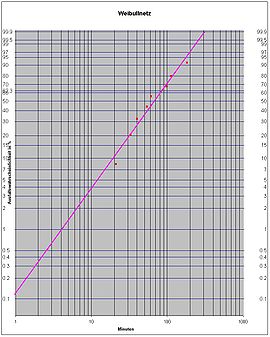
Trägt man die Verteilung in der Form
auf, ergibt sich eine Gerade, bei der man den Parameter b leicht als Steigung ablesen kann. Der Parameter T kann dann folgendermaßen berechnet werden:
Hierbei bezeichnet a den y-Achsenabschnitt.
Oft kommt es vor, dass trotz Beanspruchung erst nach einer Betriebszeit t0 Ausfälle überhaupt eintreten (Bremsbelag verschlissen, ...). Auch dies kann in der Weibull-Verteilungsfunktion berücksichtigt werden. Sie hat dann folgendes Aussehen:
Trägt man die Funktion wieder auf, ergibt sich keine Gerade, sondern eine nach oben konvexe Kurve. Verschiebt man alle Punkte um den Wert t0, so geht die Kurve in eine Gerade über.
Eigenschaften
Erwartungswert
Den Erwartungswert erhält man zu
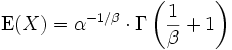 .
.
Varianz
Die Varianz bestimmt sich zu
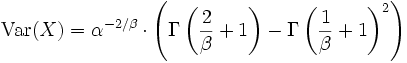 ,
,
wobei Γ die Gammafunktion bezeichnet.
Schiefe
Die Schiefe ergibt sich zu
Beziehung zu anderen Verteilungen
Beziehung zur Exponentialverteilung
- Man sieht, dass der Fall β = 1 die Exponentialverteilung
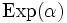 ergibt. Mit anderen Worten: Die Exponentialverteilung behandelt Probleme mit konstanter Ausfallrate λ. Untersucht man jedoch Fragestellungen mit steigender (β > 1) oder fallender (β < 1) Ausfallrate, dann geht man von der Exponentialverteilung zur Weibull-Verteilung über.
ergibt. Mit anderen Worten: Die Exponentialverteilung behandelt Probleme mit konstanter Ausfallrate λ. Untersucht man jedoch Fragestellungen mit steigender (β > 1) oder fallender (β < 1) Ausfallrate, dann geht man von der Exponentialverteilung zur Weibull-Verteilung über. - Ist der Parameter β > 1, dann wird ein System mit einer mit der Zeit ansteigenden Ausfallrate, also ein alterndes System, beschrieben.
- Besitzt X eine Exponentialverteilung
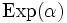 mit Parameter α, dann besitzt die Zufallsvariable
mit Parameter α, dann besitzt die Zufallsvariable 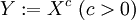
eine Weibull-Verteilung
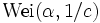 . Zum Beweis betrachte man die Verteilungsfunktion von Y:
. Zum Beweis betrachte man die Verteilungsfunktion von Y: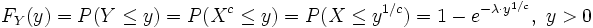 .
.
Das ist die Verteilungsfunktion einer Weibull-Verteilung.
Gestreckte Exponentialfunktion
Die Funktion
ist als gestreckte Exponentialfunktion bekannt.
Siehe auch
Literatur
- Lindgren, Bernard W.: Statistical Theory, New York etc., 1993
- Fisz, Marek: Wahrscheinlichkeitsrechnung und mathematische Statistik, Berlin 1970
- Hartung, Joachim, Elpelt, Bärbel, Klösener, Karl-Heinz: Statistik, München 2002
- Rinne, Horst, Mittag, Hans-Joachim: Statistische Methoden der Qualitätssicherung, München, Wien 2002
- Wilker, Holger: Weibull-Statistik in der Praxis, Leitfaden zur Zuverlässigkeitsermittlung technischer Produkte, Norderstedt 2004
Weblinks
- Weibull-Verteilung in der Zuverlässigkeitsanalyse
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.


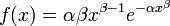
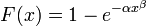
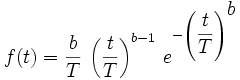
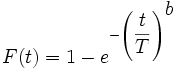
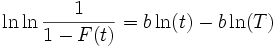
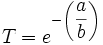
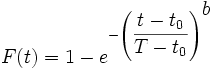
![\operatorname{v}(X)=\frac{\left(\frac{1}{\beta}+1\right)\left[\frac{2}{\beta}+1-\Gamma\left(\frac{1}{\beta}+1\right)\right]}
{\left(\frac{1}{\beta}+1-\Gamma\left(\frac{1}{\beta}+1\right)\right)^{\frac{3}{2}}\Gamma^{\frac{1}{2}}\left(\frac{1}{\beta}+1\right)}-2\frac{\Gamma^{\frac{1}{2}}\left(\frac{1}{\beta}+1\right)}
{\left(\frac{1}{\beta}+1-\Gamma\left(\frac{1}{\alpha}+1\right)\right)^{\frac{1}{2}}}](/pictures/dewiki/99/c52cf898f3352d58ede3b9e5360769a0.png)