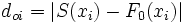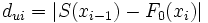Kolmogoroff-Smirnow-Test

Der Kolmogorow-Smirnow-Anpassungstest, KS-Test oder KSA-Test (nach Andrei Nikolajewitsch Kolmogorow und Nikolaj Wassiljewitsch Smirnow) ist ein statistischer Test auf Übereinstimmung zweier Wahrscheinlichkeitsverteilungen. Das kann ein Vergleich der Verteilungen zweier Stichproben sein (zweiseitiger KS-Test), aber auch der Test darauf, ob eine Stichprobe einer zuvor angenommenen Wahrscheinlichkeitsverteilung folgt (einseitiger KS-Test). Speziell bei letzterem ist der KS-Test im Gegensatz zum χ²-Test auch für kleine Stichproben geeignet.

Der Kolmogorow-Smirnow-Test ist als nichtparametrischer Test sehr stabil und unanfällig. Ursprünglich wurde der Test für stetig verteilte metrische Merkmale entwickelt; er kann aber auch für diskrete und sogar rangskalierte Merkmale verwendet werden. In diesen Fällen ist der Test etwas weniger trennscharf, d.h. die Nullhypothese wird seltener abgelehnt als im stetigen Fall.

Ein großer Vorteil besteht darin, dass die zugrundeliegende Zufallsvariable keiner Normalverteilung folgen muss. Die Verteilung der Prüfgröße d_n ist für alle (stetigen) Verteilungen identisch. Dies macht den Test vielseitig einsetzbar, bedingt aber auch seinen Nachteil, denn der KS-Test ist nicht sehr genau.

Konzeption

Die Konzeption soll anhand des Anpassungstests erläutert werden, wobei der Vergleich zweier Merkmale analog zu verstehen ist. Man betrachtet ein statistisches Merkmal X, dessen Wahrscheinlichkeiten in der Grundgesamtheit unbekannt sind. Es wird bezüglich der Wahrscheinlichkeiten von X eine Nullhypothese

H₀: Das Merkmal X hat die Wahrscheinlichkeitsverteilung F₀(x)

aufgestellt.

Nach dem Gliwenko-Cantelli-Satz strebt die empirische Verteilung gleichmäßig gegen die Verteilungsfunktion von X (also unter H₀ gegen F₀). Wählt man 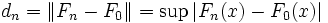$d_n=\|F_n-F_0\|=\sup|F_n(x)-F_0(x)|$ als Teststatistik, so sollte man unter H₀ kleine Werte bekommen. Diese Teststatistik ist unabhängig von der Verteilung. Wenn sie kleiner ist als der tabellierte kritische Wert, so wird die Nullhypothese von diesem Test nicht verworfen.

Vorgehensweise beim einseitigen KS-Test

Von einer Zufallsvariablen X liegen n Beobachtungen x_i (i = 1,...,n) vor. Von diesen Beobachtungen wird die relative Summenfunktion (Summenhäufigkeit, empirische Verteilungsfunktion) S(x_i) ermittelt. Diese empirische Verteilung wird nun mit der entsprechenden hypothetischen Verteilung der Grundgesamtheit verglichen: Es wird der Wert der Wahrscheinlichkeitsverteilung an der Stelle x_i bestimmt: F₀(x_i). Wenn X tatsächlich dieser Verteilung gehorcht, müssten die beobachtete Häufigkeit S(x_i) und die erwartete Häufigkeit F₀(x_i) in etwa gleich sein.

Es wird also für jedes i die absolute Differenz

$d_{oi} = |S(x_i)-F_0(x_i)|~$

und auch

$d_{ui} = |S(x_{i-1})-F_0(x_i)|~$

berechnet. Es wird sodann die absolut größte Differenz d_max aus allen Differenzen ermittelt. Wenn d_max also einen kritischen Wert d_α übersteigt, wird die Hypothese bei einem Signifikanzniveau α abgelehnt.

Bis n=40 liegen die kritischen Werte tabelliert vor Tabelle. Für größere n werden sie näherungsweise mit Hilfe einer einfachen Formel bestimmt.

Hier die Konfidenz-Intervalle bei d_max (für n>40):

Signifikanz-Niveau α	dmax
20%	1.07/√n
10%	1.22/√n
5%	1.36/√n
2%	1.52/√n
1%	1.63/√n

Anwendungsbeispiel

Der Kolmogorow-Smirnow-Test kann zum Testen von Zufallszahlen genutzt werden, beispielsweise ob die Zufallszahlen einer bestimmten Verteilung (z. B. Gleichverteilung) folgen.

Zahlenbeispiel

Grafik zu diesem Zahlenbeispiel. Links ein Histogramm, rechts die tatsächliche und die empirische Verteilungsfunktion

In einem Unternehmen, das hochwertige Parfüms herstellt, wurde im Rahmen der Qualitätssicherung an einer Abfüllanlage die abgefüllte Menge für n=8 Flakons gemessen. Es ist das Merkmal x: abgefüllte Menge in ml.

Es soll geprüft werden, ob noch die bekannten Parameter der Verteilung von X gelten.

Zunächst soll bei einem Signifikanzniveau α=0,05 getestet werden, ob das Merkmal X in der Grundgesamtheit überhaupt normalverteilt mit den bekannten Parametern μ=11 und σ=1 ist, also

H_o: F(x) = F₀(x) = Φ (x|11;1)

mit Φ als Normalverteilungssymbol. Es ergibt sich folgende Tabelle:

i	xi	S(xi)	Fo(xi)	S(xi-1)-Fo(xi)	S(xi)-Fo(xi)
1	9,41	0,125	0,056	-0,056	0,069
2	9,92	0,250	0,140	-0,015	0,110
3	11,55	0,375	0,709	-0,459	-0,334
4	11,60	0,500	0,726	-0,351	-0,226
5	11,73	0,625	0,767	-0,267	-0,142
6	12,00	0,750	0,841	-0,216	-0,091
7	12,06	0,875	0,855	-0,105	0,020
8	13,02	1,000	0,978	-0,103	0,022

Hier bezeichnen x_i die i-te Beobachtung, S(x_i) den Wert der Summenfunktion der i-ten Beobachtung und F₀(x_i) den Wert der Normalverteilungsfunktion an der Stelle x_i mit den genannten Parametern. Die nächsten Spalten geben die oben angeführten Differenzen an. Der kritische Wert, der zur Ablehnung führt ist bei α = 0,05 der Betrag 0,457. Die größte absolute Abweichung in der Tabelle ist 0,459 in der 3. Zeile. Dieser Wert ist größer als der kritische Wert, daher wird die Hypothese gerade noch abgelehnt. Es ist also zu vermuten, dass die Verteilungshypothese falsch ist. Das kann bedeuten, dass die abgefüllte Menge nicht mehr normalverteilt ist, dass sich die durchschnittliche Abfüllmenge verschoben hat oder auch, dass sich die Varianz der Abfüllmenge verändert hat.

Weblinks

• Beschreibung des Tests
• Tabelle mit kritischen Werten
• Tabelle der kritischen Werte
• Online Durchführung des Tests