komplanar — kom|pla|nar 〈Adj.; Math.〉 sich in der gleichen Ebene befindend * * * komplanar [zu lateinisch complanare »einebnen«], in der gleichen Ebene liegend. So sind z. B. die Ecken eines Quadrats komplanar, die eines Würfels jedoch nicht. * * *… … Universal-Lexikon
komplanar — kom|pla|nar 〈Adj.; Math.〉 sich in der gleichen Ebene befindend [Etym.: zu lat. complanare »einebnen«] … Lexikalische Deutsches Wörterbuch
komplanar — kom|pla|nar* <zu lat. complanare »einebnen, dem Erdboden gleichmachen«; vgl. ↑...ar> in der gleichen Ebene liegend (z. B. von ↑Vektoren; Math.) … Das große Fremdwörterbuch
Komplanarität — oder Koplanarität ist ein Begriff aus der Geometrie einem Teilbereich der Mathematik. Mehrere Punkte heißen komplanar, wenn sie in einer Ebene liegen. Drei Vektoren gelten als komplanar, wenn sie linear abhängig sind. Einer der drei Vektoren… … Deutsch Wikipedia
Koplanar — Komplanarität oder Koplanarität ist ein Begriff aus der Geometrie einem Teilbereich der Mathematik. Mehrere Punkte heißen komplanar, wenn sie in einer Ebene liegen. Drei (oder mehr) Vektoren gelten als komplanar, wenn sie linear abhängig sind.… … Deutsch Wikipedia
Koplanarität — Komplanarität oder Koplanarität ist ein Begriff aus der Geometrie einem Teilbereich der Mathematik. Mehrere Punkte heißen komplanar, wenn sie in einer Ebene liegen. Drei (oder mehr) Vektoren gelten als komplanar, wenn sie linear abhängig sind.… … Deutsch Wikipedia
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Euklidisch — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Fehlstand — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Glossar mathematischer Attribute — Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik zur Löschung vorgeschlagen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel… … Deutsch Wikipedia
 . Für die Komplanarität muss die Gleichung
. Für die Komplanarität muss die Gleichung 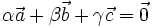 mit
mit  erfüllbar sein, wobei α,β,γ nicht gleichzeitig 0 sein dürfen. Die Lösung lässt sich mittels eines linearen Gleichungssystems mit n Gleichungen und den Unbekannten α,β,γ ermitteln.
erfüllbar sein, wobei α,β,γ nicht gleichzeitig 0 sein dürfen. Die Lösung lässt sich mittels eines linearen Gleichungssystems mit n Gleichungen und den Unbekannten α,β,γ ermitteln.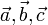 sind komplanar wenn
sind komplanar wenn  .
.