Konkaves Drachenviereck

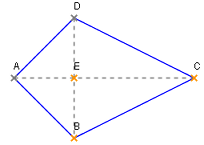
Ein Drachenviereck (in der Mathematik: Deltoid) ist ein ebenes Viereck,

• bei dem eine Diagonale Symmetrieachse ist,

oder (äquivalent)

• das zwei Paare gleich langer benachbarter Seiten besitzt.

Oft wird nur die konvexe Form des Deltoids als Drachenviereck bezeichnet und die nicht-konvexe Form (mit einer konkaven Ecke) als Pfeilviereck. (Die Bezeichnung „Drachenviereck“ verweist auf die Form vieler Flugdrachen.)

Für jedes Deltoid gilt:

• die Diagonalen stehen aufeinander senkrecht (sie sind orthogonal: das Deltoid ist ein orthodiagonales Viereck)
• eine Diagonale halbiert die andere
• die einander gegenüberliegenden Winkel in den Eckpunkten B und D sind gleich groß
• die Diagonale durch die Eckpunkte A und C halbiert in diesen die Winkel

Für jedes konvexe Deltoid gilt:

• es hat einen Inkreis und ist daher ein Tangentenviereck.
• es hat auch einen Umkreis, wenn die beiden gleichen Eckwinkel (in B und D) rechte Winkel (je 90°) sind.

Eine spezielles Drachenviereck ist der Rhombus (auch Raute): er ist ein gleichseitiges Deltoid.

Eine Verallgemeinerung des Drachenvierecks ist der schiefe (schräge) Drachen, bei dem nur verlangt wird, dass eine Diagonale durch die andere halbiert wird. Das Deltoid ist dann ein gerader Drachen.

Konvexe Vierecke

Quadrat | Rechteck | Raute | Parallelogramm | Drachenviereck | Trapez | Sehnenviereck | Tangentenviereck