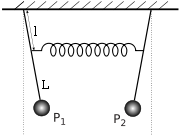
Koppelschwingungl

Beispiel für ein gekoppeltes Pendel

Zwei Pendel, zwischen denen ein Energieaustausch stattfinden kann (beispielsweise durch eine Schraubenfeder), werden als gekoppelte Pendel bezeichnet; die ausgeführten Schwingungen werden auch als Koppelschwingung bezeichnet. In jedem Pendel wirkt ein Richtmoment, das durch die Schwerkraft hervorgerufen wird und bestrebt ist, das Pendel in die Ruhelage zurückzuziehen. Außerdem macht sich die vorhandene Kopplung in Form eines zusätzlichen Richtmoments bemerkbar, das so wirkt, dass die Feder möglichst entspannt wird.

Historische Beobachtungen

Der niederländische Astronom und Physiker Christiaan Huygens beobachtete bereits im 17. Jahrhundert gekoppelte Pendelschwingungen, als er feststellte, dass zwei baugleiche Pendeluhren, die an Bord eines Schiffes in einem gemeinsamen Gehäuse eingebaut waren, nach einer halben Stunde synchron schwangen, egal in welcher Ausgangsposition sich die Pendel zu Beginn befanden. Die Pendelgewichte übertrugen Energie an das Uhrengehäuse und beeinflussten sich dabei gegenseitig. (siehe: Lock-in-Effekt)

Physikalisch-mathematische Betrachtung

gekoppelte Pendel in Ruhelage durch Moment der Feder

Betrachten wir als Modell den Fall zweier durch eine Feder gekoppelter Pendel. Dann werden aufgrund des Drehmomentes, verursacht durch die Schwerkraft und des entgegengesetzt wirkenden Momentes der Feder, die beiden Pendel in eine neue Gleichgewichtslage ausgelenkt.

Lenkt man nun Pendel 2 um den Winkel θ₂ nach rechts aus, erhält man, falls die Auslenkung klein war, ein Gesamtmoment von:

$M_2=-mgL \cdot \theta_2-k \cdot l^2 \cdot \theta_2$

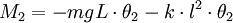
wobei k die Federkonstante der Kopplungsfeder ist.

Lenkt man jetzt zusätzlich Pendel 1 um θ₁ nach links aus, ergibt sich ein Gesamtmoment von:

$M_2=-mgL \cdot \theta_2-k \cdot l^2 \theta_2+k \cdot l^2 \theta_1 = J \ddot{\theta}_2$

Analog kann man für Pendel 1 verfahren und erhält die beiden Differentialgleichungen:

$J \ddot{\theta}_1=-mgL \cdot \theta_1+k \cdot l^2 (\theta_2-\theta_1)$

$J \ddot{\theta}_2=-mgL \cdot \theta_2-k \cdot l^2 (\theta_2-\theta_1)$

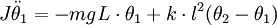
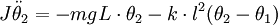
J ist dabei das Trägheitsmoment eines Pendels. Falls es sich um ein Fadenpendel handelt, gilt J = mL².

Man erhält drei charakteristische Schwingungsformen des Pendelsystems:

Beispiel: gekoppeltes Pendel als Eigenwertproblem - Normalschwingungsanalyse

Am einfachsten gelangen wir zu den Bewegungsgleichungen des gekoppelten Pendels im Lagrange-Formalismus. Hierzu ist es zunächst einmal notwendig, die Lagrange-Funktion des Systems aufzustellen:

$\mathcal{L}=T-U$

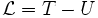
wobei T, die kinetische Energie des Systems, gegeben ist durch:

$T=\frac{1}2 m_1 L^2\cdot\dot\theta_1^2 + \frac{1}2 m_2 L^2 \cdot\dot\theta_2^2$

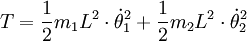
und U, die potentielle Energie des Systems, gegeben ist durch:

$U=m_1 g L\cdot\cos(\theta_1)+ m_2 g L\cdot\cos(\theta_2) + \frac{1}2 kl^2\cdot\left(\sin\theta_{1}-\sin\theta_{2}\right)^{2}$

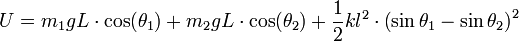
woraus folgt:

$\mathcal{L}=\frac{1}2 m_1 L^2 \cdot\dot\theta_1^2 + \frac{1}2 m_2 L^2 \cdot\dot\theta_2^2 - m_1 g L \cdot\cos(\theta_1) - m_2 g L \cdot\cos(\theta_2) - \frac{1}2 k l^2 \cdot\left(\sin\theta_{1}-\sin\theta_{2}\right)^{2}$

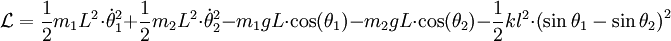
Mit der Euler-Lagrange-Gleichung:

$\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial \mathcal{L}}{\partial \dot\theta_i}-\frac{\partial \mathcal{L}}{\partial \theta_i}=0$

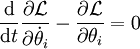
und der Näherung 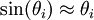$\sin(\theta_i)\approx\theta_i$ sowie $\cos(\theta_i)\approx 1 - \frac{\theta_i^2}{2}$ (für kleine Auslenkungen) gelangen wir auf zwei gekoppelte Bewegungsgleichungen der Form:

$\ddot\theta_1 + \frac{g}L\cdot\theta_1 + \frac{k l^2}{m_1 L^2}\cdot (\theta_1-\theta_2)=0$

$\ddot\theta_2 + \frac{g}L\cdot\theta_2 - \frac{k l^2}{m_2 L^2}\cdot (\theta_1-\theta_2)=0$

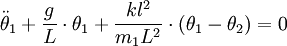
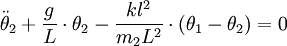
Mit dem Ansatz, dass jede Fundamentalschwingung der hier beschriebenen Normalschwingung die Form:

$\theta_i(t) = a_i\cdot\cos(\omega t + \beta_i)$

hat, wird folgende Matrixdarstellung induziert:

$\underbrace {\begin{pmatrix} {(\frac{g}{L}+\frac{k l^2}{m_1 L^2})-\omega^2} & {-\frac{k l^2}{m_1 L^2}} \\ {-\frac{k l^2}{m_2 L^2}} & {(\frac{g}{L}+\frac{k l^2}{m_2 L^2})-\omega^2} \end{pmatrix}}_{A}\begin{pmatrix} a_{i1} \\ a_{i2} \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}$

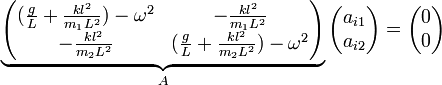
Mit dem Ansatz:

det(A) = 0

ermittelt man die Eigenwertsquadrate also ω². Beispielsweise für den Spezialfall m₁ = m₂ = m:

$\omega_{1/2}^2=\frac{g}{L}+\frac{k l^2}{m L^2}\pm \frac{k l^2}{m L^2}$

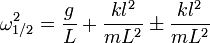
Zu den Eigenwerten sind nun noch die Eigenvektoren zu bestimmen. Für dieses Beispiel:

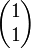$\begin{pmatrix} 1 \\ 1 \end{pmatrix}$ und $\begin{pmatrix} 1 \\ -1 \end{pmatrix}$

Somit ergibt sich die Lösung der Normalschwingungsanalyse (Eigenwertproblem) für den Spezialfall zu:

$\vec\theta(t)=A_1\begin{pmatrix} 1 \\ 1 \end{pmatrix}\cos(\omega_1 t+\beta_1)+A_2\begin{pmatrix} 1 \\ -1 \end{pmatrix}\cos(\omega_2 t+\beta_2)$

Fallunterscheidungen

Die Variablen A₁ und A₂ kann man mit der nachstehenden Grafik diskutieren. Bild 1 zeigt den Fall, dass A₂ = 0; Bild 2 zeigt den Fall, dass A₁ = 0 und Bild 3 zeigt den Fall, dass $\scriptstyle A_1 , A_2\ne 0$.

Bild 1: Gleichsinnige Schwingung

Die beiden Pendel schwingen mit gleicher Amplitude und gleicher Phase.

Bild 2: Gegensinnige Schwingung

Die beiden Pendel schwingen mit gleich großer Amplitude aber in Gegenphase.

Bild 3: Schwebungsfall

Wird zu Beginn nur eines der beiden Pendel aus seiner Ausgangslage ausgelenkt, so wandert die Schwingungsenergie langsam zwischen den beiden Pendeln hin und her.

Gekoppelte Pendel im Dynamikum

Weblinks

• zu Huygens Beobachtung
• Experiment
• Experiment