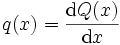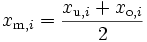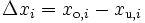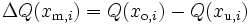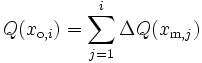- Korngrößenanalyse
-
Die Aufgabe der Dispersitätsanalyse liegt in der Beschreibung und Messung disperser Stoffsysteme. Das sind Systeme aus mindestens zwei Komponenten gleichen oder verschiedenen Aggregatzustandes, von denen mindestens eine Komponente in verteilter (disperser) Form vorliegt. Andere Bezeichnungen für die Dispersitätsanalyse sind Granulometrie, Kornanalyse, Korngrößenanalyse oder Teilchengrößenanalyse, englisch Particle Size Analysis. Auch die Bezeichnung Partikelmesstechnik ist gebräuchlich, obwohl eine Analyse mehr ist als Messtechnik und Dispersität mehr als eine Menge von Partikeln.
Beispiele für disperse Systeme sind:
- Staub (Aerosole) in der Luft
- Nebel, Wolken
- Blutkörperchen im Blut
- Fetttröpfchen in der Milch
- Rosinen im Kuchen
- Pigmente in Anstrichen
- Kies im Beton
- Bläschen im Sekt
- Schnee auf einem Hang
Gelegentlich interessiert nur die disperse Komponente, insbesondere im Haufwerk:
- Sedimente (insbesondere Boden)
- die meisten Gesteine (vor allem Sedimentgesteine und Plutonite, Geröll und Lockergestein, Geschiebe in der Limnologie)
- Puder und Pulver, etwa Zucker (Puderzucker, Kristallzucker, Kandiszucker, Würfelzucker)
- Schüttungen, etwa Koks auf der Halde, oder Müll auf einer Deponie
Die Dispersitätsanalyse untersucht Größe und Form der dispersen Elemente, ihre Konzentration und ihre räumliche Verteilung. Diese Größen sind in der Regel statistisch verteilt und bei einigen Systemen zeitabhängig.
Kennzeichnung von Einzelelementen
Zur Kennzeichnung von Einzelelementen bedient man sich einer einzelnen charakteristischen Größe (Korn-, Teilchen-, Partikelgröße). Meist ist dies ein typischer Durchmesser eines Partikels, wobei der Durchmesser (Äquivalentdurchmesser) anhand einer charakteristischen Eigenschaft bestimmt wird, beispielsweise über den Durchmesser einer volumen- oder oberflächengleichen Kugel, über den Durchmesser einer Kugel mit gleicher Sinkgeschwindigkeit oder ähnlichem. Bei groben Einzelelementen kommt auch die Masse in Frage, die den Vorzug hat, von irgendwelchen Annahmen unabhängig zu sein.
Korngrößenverteilungen
Ein disperses System setzt sich in der Regel aus Teilchen verschiedener Korngrößen zusammen. Eine Korngrößenverteilung ist eine statistische Beschreibung der Größenverteilung der Partikel in einem solchen System. Dabei gibt die Summenhäufigkeitsverteilung Q(x) an, welcher Anteil am Gesamtsystem kleiner oder gleich der Teilchengröße x ist.
Die Häufigkeitsdichte kann durch Ableiten der Summenhäufigkeitsverteilung berechnet werden:
In vielen Fällen ist es nicht möglich, die Korngrößenverteilung kontinuierlich zu verwenden bzw. zu messen. Dann wird die kontinuierliche Verteilung durch eine diskrete Verteilung ersetzt, bei der einzelne Größenklassen vorkommen.
Jede einzelne Klasse i besitzt die folgenden charakteristischen Größen:
- untere Klassengrenze xu,i
- obere Klassengrenze xo,i
- Klassenmittel xm, i:
- Klassenbreite Δxi:
- Klassenhäufigkeit ΔQ:
- Summenhäufigkeit Q:
Es ist sinnvoll, alle Größen, die sich auf eine einzelne Klasse beziehen, auf den Klassenmittelwert xm, i zu beziehen und alle Größen, die sich auf eine Reihe von Klassen beziehen, auf die Obergrenze der größten Klasse.
Praktisch ermittelt man die Korngrößenverteilung meist durch Siebanalyse (Sieblinie), Sedimentation, Windsichten oder optische Verfahren, wie z.B. Digitale Bildverarbeitung oder Laserlichtstreuung. Es gibt eine Vielzahl weiterer Verfahren, die auf bestimmte Stoffe oder Größenbereiche beschränkt sind.
In durch Sedimentation nach Korngröße sortiertem Material verwendet man das Körnungsnetz, etwa in der Bodenkunde nach DIN 18123.
In manchen Zusammenhängen werden disperse Systeme durch Mittelwerte gekennzeichnet, deren wichtigster die spezifische, das heißt massen- oder volumenbezogene Oberfläche ist.
Literatur
- DIN 66111 Sedimentationsanalyse, Grundlagen
- DIN 66118 Sichtanalyse, Grundlagen
- DIN 66141 Darstellung von Korn-(Teilchen-)größenverteilungen, Grundlagen
- DIN 66160 Messen disperser Systeme, Begriffe
- DIN 66161 Partikelgrößenanalyse, Formelzeichen, Einheiten
- DIN 66165 Siebanalyse, Grundlagen, Durchführung
- W. Alex: Krümelkunde – Gemeinfassliche Darstellung des Krümelwesens und verwandter Gebiete. Skriptum, 8. August 2006 (Webdokument, pdf 1,4 MB)
- M. Stieß: Mechanische Verfahrenstechnik 1 Springer-Verlag, Berlin 1995/2008, ISBN 978-3-540-32551-2
- Das 1x1 der optimalen Siebanalyse
Wikimedia Foundation.