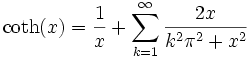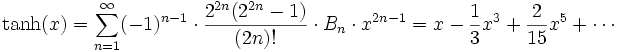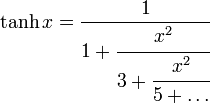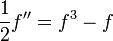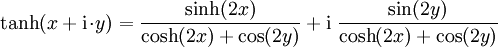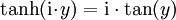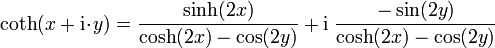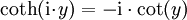- Kotangens Hyperbolicus
-
Tangens Hyperbolicus und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens.
Inhaltsverzeichnis
Schreibweisen
Tangens Hyperbolicus: 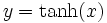
Kotangens Hyperbolicus: 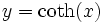
Definitionen
Eigenschaften
Tangens Hyperbolicus Kotangens Hyperbolicus Definitionsbereich 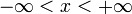
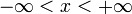 ;
; 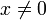
Wertebereich 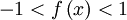
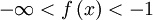 ;
; 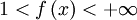
Periodizität keine keine Monotonie streng monoton steigend x < 0 streng monoton fallend
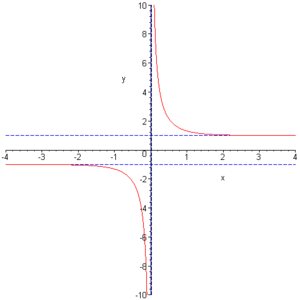
x > 0 streng monoton fallendSymmetrien Punktsymmetrie zum Koordinatenursprung Punktsymmetrie zum Koordinatenursprung Asymptoten 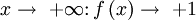
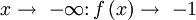
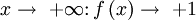
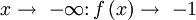
Nullstellen x = 0 keine Sprungstellen keine keine Polstellen keine x = 0 Extrema keine keine Wendepunkte 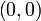
keine Spezielle Werte
mit dem goldenen Schnitt
 .
.Der Kotangens Hyperbolicus hat einen Fixpunkt, d.h. es gibt ein u, sodass
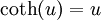 . Er liegt bei u * = 1,19967874 (Folge A085984 in OEIS)
. Er liegt bei u * = 1,19967874 (Folge A085984 in OEIS)Umkehrfunktionen
Der Tangens Hyperbolicus ist eine Bijektion
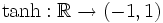 . Die Umkehrfunktion nennt man Areatangens Hyperbolicus und ist für Zahlen x aus dem Intervall ( − 1,1) definiert und nimmt als Wert alle reellen Zahlen an. Sie lässt sich durch den natürlichen Logarithmus ausdrücken:
. Die Umkehrfunktion nennt man Areatangens Hyperbolicus und ist für Zahlen x aus dem Intervall ( − 1,1) definiert und nimmt als Wert alle reellen Zahlen an. Sie lässt sich durch den natürlichen Logarithmus ausdrücken:Für die Umkehrung des Kotangens Hyperbolicus gilt:
Ableitungen
Die n-te Ableitung ist gegeben durch
Additionstheorem
Es gilt das Additionstheorem
Integrale
Weitere Darstellungen
Reihenentwicklungen
Der Anfang der Taylorreihe des Tangens Hyperbolicus lautet:
Die Bn sind die Bernoulli-Zahlen. Der Konvergenzradius dieser Reihe ist π / 2.
Kettenbruchdarstellung
Gauß zeigte folgende Formel:
Differentialgleichung
tanh löst folgende Differentialgleichung:
mit f(0) = 0 und
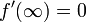
Komplexe Argumente
Siehe auch
Weblinks
- Eric W. Weisstein: Hyperbolic Tangent und Hyperbolic Cotangent auf MathWorld
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.

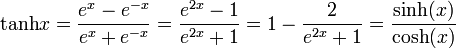
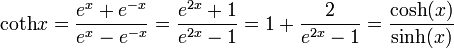

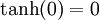
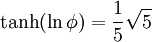
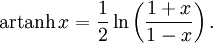
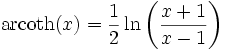
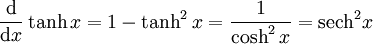
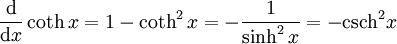
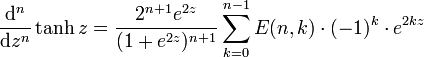
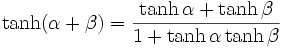
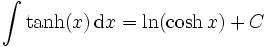
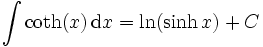
![\operatorname{tanh}(x) = \sgn(x) \left[1+ \sum_{k=1}^\infty (-1)^k2e^{-2k|x|}\right]](/pictures/dewiki/98/bfc9b05b45f3a3a9d065317bca6e0417.png)