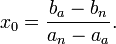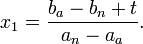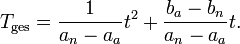Lafferkurve

Laffer-Kurve. Der Scheitelpunkt der Parabel ist rein hypothetisch.

Die Laffer-Kurve (ca. 1974) beschreibt einen nach dem Ökonomen Arthur B. Laffer benannten Zusammenhang zwischen Steuersatz und Steuereinnahmen. Die Idee tauchte bereits in Jonathan Swifts Steuereinmaleins (1728) auf.

Wirkung

Wird der Steuersatz, ausgehend von einem Satz von Null, sukzessive erhöht, so steigen auch die Steuereinnahmen in einer Volkswirtschaft, allerdings nur bis zu einem bestimmten Punkt. Wird der Steuersatz über diesen Punkt hinaus weiter in Richtung 100 % erhöht, dann nehmen die Steuereinnahmen wieder ab. Dieses Phänomen entsteht, weil höhere Steuersätze zu einem Rückgang des volkswirtschaftlichen Outputs führen können. Dieses wiederum kann u. a. auf einen verminderten Arbeitseinsatz zurückgeführt werden. Die Laffer-Kurve unterstellt allerdings dabei, dass die laufende Leistungserstellung eines Betriebes vom Unternehmer selbst determiniert würde und nicht als Reaktion auf die Marktnachfrage erfolge.

In der Volkswirtschaft findet diese Theorie nur verminderten Anklang, da Lage und Scheitelpunkt der Kurve (also der maximale Steuerertrag) nicht genau definiert werden können, da die Kurve hypothetischen Grundlagen folgt. Es lassen sich daher mathematisch auch nur 2 Punkte auf der Kurve bestimmen:

Beträgt der Steuersatz t 0 %, so ist das Steueraufkommen T am Volkseinkommen Y demnach auch 0.

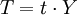$T = t \cdot Y$ entspricht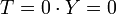 $T = 0 \cdot Y = 0$

Beträgt der Steuersatz 100 %, so ist das Steueraufkommen am Volkseinkommen ebenfalls 0.

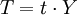$T = t \cdot Y$ entspricht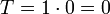 $T = 1 \cdot 0 = 0$

Das gesamte Volkseinkommen kommt als Steuern dem Staat zugute. Da an diesem Punkt aber Y = 0 betrüge, ist so eine Volkswirtschaft nicht mehr vorstellbar, da den Wirtschaftssubjekten kein Geld zur Deckung ihres (lebenswichtigen) Konsums bliebe. Daher setzt die Laffer-Kurve an diesem Punkt auch die Steuereinnahmen auf Null.

Beispiele

Ein Beispiel für die von Laffer beschriebene Theorie lässt sich (stark vereinfacht) an der Tabaksteuererhöhung in Deutschland ablesen:

Obwohl die Steuereinnahmen nach den Steuererhöhungen auf Tabakwaren, insbesondere Zigaretten, steigen müssten, sind diese im ersten Halbjahr 2005 gefallen. Viele Menschen konsumieren nun alternative, niedriger besteuerte Tabakprodukte, wie Schnittabak oder beschaffen sich Schmugglerware (vgl. Prohibitivpreis). Dieser Zustand wird durch einen Punkt auf der Laffer-Kurve rechts des Scheitelpunkts beschrieben. Aussagen, ein bestimmter Preis p(x) garantiere maximale Steuereinnahmen oder ein bestimmter Preis p(y) würde alle Raucher zum Aufhören (also T = 0) bringen, ließen sich erneut nur nach aufwendigen empirischen Studien halten.

Ein anderes Beispiel bietet die Senkung des Körperschaftsteuersatzes in Irland auf nur 12,5 % und die folgende Vervielfachung des selbigen Aufkommens – wohl aber insbesondere durch die Ansiedlung ausländischer Unternehmen.

Laffers theoretischer Zusammenhang, den er laut eigenen Angaben zum ersten Mal auf einer Serviette eines Washingtoner Restaurants skizzierte, wurde vor allem unter angebotsseitigen Ökonomen populär. Die oft als Reaganomics bezeichnete Wirtschaftspolitik von US-Präsident Ronald Reagan wurde durch Laffer maßgeblich beeinflusst. Die keynesianische Fiskalpolitik stützt ihre Argumentation dagegen auf das Haavelmo-Theorem.

Eine modelltheoretische Lafferkurve lässt sich aus dem Grundmodell der Preisbildung auf Märkten durch Angebot und Nachfrage mathematisch herleiten unter der Annahme der Bedingungen des vollkommenen Marktes.

Im Diagramm Menge x über Preis p gelte ferner: Die Nachfragekurve N lässt sich darstellen als fallende Gerade der Gestalt y_n = a_nx + b_n , wobei a_n < 0.

Die Angebotskurve A₀ lässt sich darstellen als steigende Gerade der Gestalt y_a = a_ax + b_a , wobei a_a > 0 Außerdem sei $b_n&amp;amp;gt; b_a \geq 0$

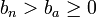
Im Schnittpunkt der beiden Geraden, dem Marktgleichgewicht, wird die Menge x₀ zum Preis p₀ abgesetzt. Mathematisch gilt für das Gleichgewicht:

a_nx + b_n = a_ax + b_a,

$x_0 = \frac{ b_a- b_n} { a_n- a_a}.$

Es wird nun angenommen, dass der Staat beabsichtigt, eine Steuer t bei den Anbietern des Marktes zu erheben, die pro abgesetzter Mengeneinheit x an den Staat zu entrichten ist. Die Einführung der Steuer t führt zu einer Parallelverschiebung der Angebotskurve A₀ nach links. Die neue Angebotskurve A₁ hat damit die Gestalt y_a = a_ax + b_a + t.

Es bildet sich ein neues Gleichgewicht im Schnittpunkt der neuen Angebotskurve A₁ mit der unveränderten Nachfragekurve N. Mathematisch gilt für das neue Gleichgewicht:

a_nx + b_n = a_ax + b_a + t.

Es ergibt sich:

$x_1 = \frac{ b_a- b_n +t} { a_n- a_a}.$

Die gesamten Steuereinnahmen des Staats beim neuen Gleichgewichtspreis betragen

T_ges = tx₁.

und damit

$T_\text{ges}= \frac {1} { a_n- a_a} t^2 + \frac { b_a- b_n} { a_n- a_a} t.$

Ergebnis unter den getroffenen Modellannahmen:

Die Funktion der gesamten Steuereinnahmen T_ges in Abhängigkeit von der Steuerhöhe t ergibt eine Parabel, die Lafferkurve. Die Parabel ist nach unten geöffnet. Die Nullstellen der Parabel liegen bei T_ges = 0.

Nach der Lösungsformel quadratischer Gleichungen liegt die 1. Nullstelle bei t₁ = 0 und die 2. Nullstelle bei t₂ = (b_n − b_a)

Das Maximum der Parabel liegt bei $t = \frac 1 2 (b_n-b_a)$.

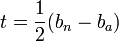Literatur

• Jochen Schumann u.a.: Grundzüge der mikroökonomischen Theorie. Springer, Berlin 1999. ISBN 3-540-660-81X.
• Gustav Dieckheuer: Makroökonomik. Theorie und Politik. 5. Auflage. Springer, Berlin 2003. ISBN 3-540-005-641.

• E. Görgens; K. Ruckriegel; F. Seitz: Europäische Geldpolitik. 4. Auflage Lucius & Lucius Verlagsgesellschaft mbH, Stuttgart 2004. ISBN 3-8282-0286-1

• Gudehus, Timm, Dynamische Märkte, Praxis, Strategien und Nutzen für Wirtschaft und Gesellschaft, Springer, Berlin-Heidelberg-New York, 2007, ISBN 978-3-540-72597-8 (s. S. 277ff u. Abb. 15.13)

• Laffer, Arthur B. (1981): Government Exactions and Revenue Deficiencies, In: The Cato Journal, Vol. 1, Nr. 1, 1-21.

• Laffer, Arthur B. (2004): The Laffer Curve - Past, Present, and Future.

• Henderson, David (1981): Limitations of the Laffer Curve as a Justification for Tax Cuts, The Cato Journal, Vol. 1, Nr. 1, 45-52.

• Trabandt, Mathias / Uhlig, Harald (2006): How Far Are We From The Slippery Slope? The Laffer Curve Revisited, Discussion Paper SFB 649, Humboldt-Universität zu Berlin.

• Dalamagas, Basil (1998): Endogenous growth and the dynamic Laffer curve, Applied Economics Vol. 30, Nr. 1: 63-75.

• Agell, Jonas / Persson, Mats (2001): On the analytics of the dynamic Laffer curve, Journal of Monetary Economics Vol. 48, Nr. 2, 397-414.

• Heijman, W.J.M. / van Ophem, J. A. C. (2005), Willingness to pay tax - The Laffer curve revisited for 12 OECD countries, The Journal of Socio-Economics Vol. 34, Nr. 5, 714-723.

• Becsi, Zsolt (2000): The Shifty Laffer Curve, Economic Review - Federal Reserve Bank of Atlanta Vol. 85, Nr. 3, 53-64.

• Becsi, Zsolt (2002): Public Spending, Transfers and the Laffer Curve, Working Paper Louisiana State University.

• Claessens, Stijn (1990): The Debt Laffer Curve: Some Estimates, World Development Vol. 18, Nr. 12, 1671-1677.

• Sander, H. (1990): Die „Debt-Relief-Laffer-Kurve“, Zur Ökonomik freiwilliger Schuldenrückkäufe im Rahmen des Brady-Plans, WiSt, Sept. 1990, 463-466.

• Mirowski, Philip (1982): What’s Wrong With the Laffer Curve?, Journal of Economic Issues Vol., Nr. 3, 815-828.