- Least Squares
-
Die Methode der kleinsten Quadrate (bezeichnender auch: der kleinsten Fehlerquadrate; englisch: Least Squares Method) ist das mathematische Standardverfahren zur Ausgleichungsrechnung. Es ist eine Wolke aus Datenpunkten gegeben, die physikalische Messwerte, wirtschaftliche Größen oder Ähnliches repräsentieren können. Zu dieser Punktwolke soll eine möglichst genau passende, parameterabhängige Modellkurve gefunden werden. Dazu bestimmt man die Parameter dieser Kurve numerisch, indem die Summe der quadratischen Abweichungen der Kurve von den beobachteten Punkten minimiert wird.
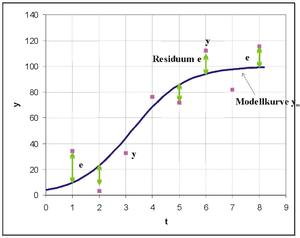 Messpunkte und deren Abstand zu einer nach der Methode der kleinsten Quadrate bestimmten Funktion. Hier wurde eine logistische Funktion als Modellkurve gewählt.
Messpunkte und deren Abstand zu einer nach der Methode der kleinsten Quadrate bestimmten Funktion. Hier wurde eine logistische Funktion als Modellkurve gewählt.In der Grafik sind Datenpunkte eingetragen. Es wurde hier eine logistische Funktion als Modellfunktion in die Punktwolke gelegt, da sie zu dem Problem und den Daten passen sollte. Die Parameter dieser Funktion werden so bestimmt, dass die Summe der Quadrate der senkrechten Abweichungen e der Beobachtungen y von der Kurve minimiert wird.
In der Stochastik wird die Methode der kleinsten Quadrate meistens als Schätzmethode in der Regressionsanalyse benutzt. Diese Bezeichnungen werden, ebenso wie Ausgleichsrechnung, häufig von den Anwendern synonym gebraucht. In der mathematischen Statistik nennt man das Verfahren auch Kleinste-Quadrate-Schätzung, während in der Physik die Bezeichnung Fitting verwendet wird. Die Fülle an Bezeichnungen demonstriert die Bedeutung und Verbreitung der Methode.
Angewandt als Systemidentifikation ist die Methode der kleinsten Quadrate in Verbindung mit Modellversuchen für Ingenieure ein Ausweg aus der paradoxen Situation, Modellparameter für unbekannte Gesetzmäßigkeiten zu bestimmen.
Inhaltsverzeichnis
Geschichtliches
Am Neujahrstag des Jahres 1801 entdeckte der italienische Astronom Giuseppe Piazzi den Asteroiden Ceres. 40 Tage lang konnte er die Bahn verfolgen, dann verschwand Ceres hinter der Sonne. Im Laufe des Jahres versuchten viele Wissenschaftler anhand von Piazzis Beobachtungen die Bahn zu schätzen (die Lösung der nichtlinearen Kepler-Gleichungen ist sehr schwierig). Die meisten Rechnungen waren unbrauchbar; als einzige war diejenige des 24jährigen Carl Friedrich Gauß genau genug (die Grundlagen schuf er schon 1795 mit 18 Jahren), um dem deutschen Astronomen von Zach zu ermöglichen, im darauffolgenden Dezember den Asteroiden wiederzufinden. Gauß erlangte dadurch Weltruhm. Sein Verfahren, die Methode der kleinsten Quadrate, publizierte er erst 1809 im zweiten Band seines himmelsmechanischen Werkes Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium. Unabhängig davon entwickelte der Franzose Adrien-Marie Legendre dieselbe Methode erstmalig im Jahre 1806 am Schluss eines kleinen Werkes über die Berechnung der Kometenbahnen und veröffentlichte eine zweite Abhandlung darüber im Jahr 1810. Von ihm stammt der Name méthode des moindres carrés (Methode der kleinsten Quadrate).
1829 konnte Gauß eine Begründung liefern, wieso sein Verfahren im Vergleich zu den anderen so erfolgreich war: Die Methode der kleinsten Quadrate ist in einer breiten Hinsicht optimal, also besser als andere Methoden. Die genaue Aussage ist als der Satz von Gauß-Markow bekannt.
Das Verfahren
Häufig ist für ein gegebenes Problem keine formelhafte Beschreibung zur Hand: Man interessiert sich für eine abhängige Variable y, deren Zustandekommen von einer vorgegebenen Variablen t oder auch von mehreren Variablen t1 bis tq abhängen kann. So hängt die Dehnung einer Feder nur von der aufgebrachten Kraft ab, der Gewinn eines Unternehmens jedoch von mehreren Faktoren wie Umsatz, Return on Investment oder Eigenkapital. Um Informationen über die Art des Zusammenhangs zu erhalten, wird man eine Messreihe y durchführen: Es werden zu verschiedenen Werten der unabhängigen Variablen tj entsprechende y-Werte erhoben. Nun wird versucht, die y-Werte mit einer Modellfunktion
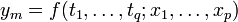 ,
,
die von q Variablen sowie p weiteren Parametern abhängen soll, gut zu approximieren.
Für die Wahl dieser Modellfunktion geht man im Allgemeinen von einem vermuteten Funktionstyp aus (beispielsweise einer Parabel oder einer Exponentialfunktion), was im Fall einer unabhängigen Variablen t meistens unproblematisch ist. Die Parameter xi dienen zur Anpassung des gewählten Funktionstyps an den beobachteten Wert y. So müsste bei der gemessenen Dehnung einer Feder die gegebene Variable Kraft durch den Parameter Federkonstante relativiert werden. Ziel ist es nun, die Parameter so zu wählen, dass die Modellfunktion die Daten bestmöglich approximiert. Zu betonen ist hierbei, dass es im Allgemeinen wesentlich mehr Datenpunkte gibt als Parameter.
Zunächst ist es nicht klar, wie man die Güte verschiedener Approximationen beurteilen soll. Gauß und Legendre hatten die Idee, Annahmen über die Messfehler zu machen. Diese sollten im Durchschnitt Null sein. Jeder Messfehler sollte die gleiche Varianz haben und von jedem anderen Messfehler stochastisch unabhängig sein. Man verlangt damit, dass in den Messfehlern keinerlei systematische Information mehr steckt, sie sollen also rein zufällig um Null schwanken. Außerdem sollten die Messfehler normalverteilt sein, was zum einen wahrscheinlichkeitstheoretische Vorteile hat und zum anderen garantiert, dass Ausreißer in y so gut wie ausgeschlossen sind.
Das Kriterium zur Bestimmung der Approximation sollte dieses also berücksichtigen und so gewählt werden, dass große Abweichungen der Modellfunktion von den Daten viel stärker bestraft werden als kleine. Mit Hilfe der Maximum-Likelihood-Methode (maximale Wahrscheinlichkeit) kann letztendlich folgende Vorschrift begründet werden: Es sollen diejenigen Parameter ausgewählt werden, bei denen die Summe der Quadrate der Abweichungen zwischen entsprechender Modellkurve und Daten (die Quadratsumme der Residuen oder auch Fehlerquadratsumme) minimal wird im Vergleich zu anderen Wahlen der Parameter, in Formelschreibweise
Äquivalent geht es darum, die euklidische Norm des Differenzvektors zu minimieren:
Wie genau dieses Minimierungsproblem gelöst wird, hängt von der Art der Modellfunktion ab. Häufig kann man mit Hilfe eines Streudiagramms zwischen tj und y schon Rückschlüsse auf den Funktionstyp ziehen.
Lineare Modellfunktion
Der zweidimensionale Fall
Ein Spezialfall der Modellfunktion ist die lineare Form, bei der die Parameter x linear eingehen. Der einfachste lineare Ansatz ist ym = x0 + x1t. Man erhält in Matrixschreibweise
Für die resultierende Ausgleichsgerade dieses einfachen (aber durchaus relevanten) Beispiels lassen sich die Lösungen für die Parameter direkt angeben als
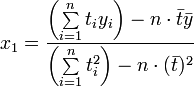 und
und 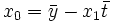
mit
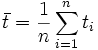 als arithmetischem Mittel der t-Werte,
als arithmetischem Mittel der t-Werte, 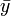 entsprechend.
entsprechend.Die Lösung für x1 kann mit Hilfe des Verschiebungssatzes auch als
angegeben werden.
Beispiel
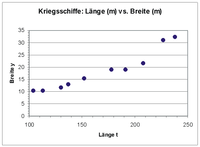
Folgendes Beispiel soll das Approximieren der linearen Funktion y = x0 + x1t zeigen. Es wurden zufällig 10 Kriegsschiffe ausgewählt und bezüglich mehrerer Merkmale darunter Länge (m) und Breite (m) analysiert. Es soll nun untersucht werden, ob die Breite eines Kriegsschiffs möglicherweise durch die Länge erklärt werden kann.
Das Streudiagramm zeigt, dass zwischen Länge und Breite eines Schiffs offensichtlich ein ausgeprägter linearer Zusammenhang besteht.
Es soll nun nach der Methode der kleinsten Quadrate eine Ausgleichsgerade errechnet werden. In der folgenden Tabelle sind die Daten zusammen mit den Zwischenergebnissen aufgeführt.
Nummer Länge (m) Breite (m) ti − t yi − y i ti yi ti* yi* ti*yi* ti*ti* yi*yi* 1 208 21,6 40,2 3,19 128,238 1616,04 10,1761 2 152 15,5 −15,8 −2,91 45,978 249,64 8,4681 3 113 10,4 −54,8 −8,01 438,948 3003,04 64,1601 4 227 31,0 59,2 12,59 745,328 3504,64 158,5081 5 137 13,0 −30,8 −5,41 166,628 948,64 29,2681 6 238 32,4 70,2 13,99 982,098 4928,04 195,7201 7 178 19,0 10,2 0,59 6,018 104,04 0,3481 8 104 10,4 −63,8 −8,01 511,038 4070,44 64,1601 9 191 19,0 23,2 0,59 13,688 538,24 0,3481 10 130 11,8 −37,8 −6,61 249,858 1428,84 43,6921 Σ 1678 184,1 0,0 0,00 3287,820 20391,60 574,8490 Man erhält nun analog zum oben angegebenen Fall zunächst
und entsprechend
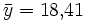 .
.
Damit bestimmt man x1 als
so dass man sagen könnte, mit jedem Meter Länge wächst ein Kriegsschiff im Durchschnitt etwa 16 Zentimeter in die Breite. Das Absolutglied x0 erhalten wir aus
wobei eine inhaltliche Interpretation aus stochastischen Gründen unterbleiben sollte. Die Anpassung der Punkte ist recht gut, es werden etwa 92 Prozent der Information in Breite mit Hilfe des Merkmals Länge erklärt.
Der allgemeine lineare Fall
Besitzt die Modellfunktion mehrere unabhängige Modellvariablen
 , erhält man eine lineare Funktion der Form
, erhält man eine lineare Funktion der Formdie auf das lineare Gleichungssystem
führt. Indem man die tij zur Datenmatrix A, die Parameter xj zum Parametervektor x und die Beobachtungen yi zum Vektor b zusammenfasst, kann man das lineare Gleichungssystem in Matrixform darstellen.
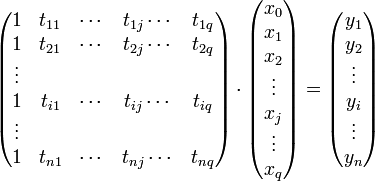 bzw.
bzw. 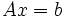 .
.
Der kleinste-Quadrate-Ansatz führt dann wieder wie oben auf ein lineares Ausgleichsproblem der Form
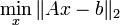 .
.
Lösung des Minimierungsproblems
Dieses Minimierungsproblem hat immer eine Lösung. Hat die Matrix A vollen Rang, so ist sie sogar eindeutig. Die partiellen Ableitungen bezüglich der xj und Nullsetzen derselben zum Bestimmen des Minimums ergeben ein lineares System von Normalgleichungen (auch Normalengleichungen)
das bei Regularität der
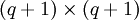 -Matrix auf der linken Seite eindeutig lösbar ist. Ferner hat die Systemmatrix ATA die Eigenschaft, positiv definit zu sein, ihre Eigenwerte sind also alle positiv. Zusammen mit der Symmetrie von ATA kann dies beim Einsatz von numerischen Verfahren zur Lösung ausgenutzt werden: beispielsweise mit der Cholesky-Zerlegung oder dem CG-Verfahren. Da beide Methoden von der Kondition der Matrix stark beeinflusst werden, ist dies manchmal keine empfehlenswerte Herangehensweise: Ist schon A schlecht konditioniert, so ist ATA quadratisch schlecht konditioniert. Eine stabilere Alternative bietet die QR-Zerlegung mit Householdertransformationen, ausgehend vom ursprünglichen Minimierungsproblem und nicht den Normalgleichungen.
-Matrix auf der linken Seite eindeutig lösbar ist. Ferner hat die Systemmatrix ATA die Eigenschaft, positiv definit zu sein, ihre Eigenwerte sind also alle positiv. Zusammen mit der Symmetrie von ATA kann dies beim Einsatz von numerischen Verfahren zur Lösung ausgenutzt werden: beispielsweise mit der Cholesky-Zerlegung oder dem CG-Verfahren. Da beide Methoden von der Kondition der Matrix stark beeinflusst werden, ist dies manchmal keine empfehlenswerte Herangehensweise: Ist schon A schlecht konditioniert, so ist ATA quadratisch schlecht konditioniert. Eine stabilere Alternative bietet die QR-Zerlegung mit Householdertransformationen, ausgehend vom ursprünglichen Minimierungsproblem und nicht den Normalgleichungen.Ferner lässt sich das Minimierungsproblem mit einer Singulärwertzerlegung gut analysieren. Diese motivierte auch den Ausdruck der Pseudoinversen, einer Verallgemeinerung der normalen Inversen einer Matrix.
In der statistischen Regressionsanalyse spricht man bei mehreren gegebenen Variablen tj von multipler Regression. Der Ansatz ist auch als OLS (ordinary least squares) bekannt, im Gegensatz zu GLS (generalised least squares), dem verallgemeinerten Regressionsmodell bei Residuen, die von der Verteilungsannahme wie Unkorreliertheit und Homoskedastie abweichen. Dagegen liegen bei multivariater Regression für jede Beobachtung i (i = 1,...,n) r viele y-Werte vor, so dass statt eines Vektors eine
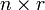 -Matrix Y vorliegt. Die linearen Regressionsmodelle sind in der Statistik wahrscheinlichkeitstheoretisch intensiv erforscht worden. Besonders in der Ökonometrie werden beispielsweise komplexe rekursiv definierte lineare Strukturgleichungen analysiert, um volkswirtschaftliche Systeme zu modellieren.
-Matrix Y vorliegt. Die linearen Regressionsmodelle sind in der Statistik wahrscheinlichkeitstheoretisch intensiv erforscht worden. Besonders in der Ökonometrie werden beispielsweise komplexe rekursiv definierte lineare Strukturgleichungen analysiert, um volkswirtschaftliche Systeme zu modellieren.Anforderungen an die Daten
Strenggenommen ist die Normalverteilungsannahme für die abhängige Variable y nicht zwingend notwendig. Es sollen lediglich keine Ausreißer vorliegen. Diese verursachen numerische Probleme, ebenso wie Multikollinearität.
Multikollinearität
Multikollinearität entsteht, wenn die Messreihen zweier gegebener Variablen ti und tj sehr hoch korreliert sind, also fast linear abhängig sind. In diesem Fall wird die Determinante von ATA sehr klein und die Lösungswerte werden unplausibel groß. Die Norm der Inversen wird umgekehrt ebenfalls sehr groß, die Kondition von ATA ist stark beeinträchtigt. Die Normalgleichungen sind dann numerisch schwer zu lösen. Häufig tritt Multikollinearität auf, wenn das Regressionsmodell durch zu viele Regressoren überbestimmt ist. Neben numerischen Alternativen können auch mit Hilfe statistischer Tests die Variablen auf ihre Erklärungswerte für das Modell hin überprüft werden und gegebenenfalls entfernt werden.
Man kann bei sehr vielen in Frage kommenden Regressoren auch schrittweise eine Variablen-Selektion durchführen:
- Bei der vorwärts gerichteten Regression (Forward Regression) wird zuerst der Regressor in das Modell aufgenommen, der den größten Beitrag zur Erklärung von y liefert, also etwa die Quadratsumme der Residuen minimiert. Dann wird unter den verbliebenen potentiellen Regressoren der Regressor ausgewählt, dessen Beitrag zum bestehenden Modell maximal ist, usw. Das Verfahren wird beendet, wenn der zusätzliche maximale Beitrag eines Regressors statistisch insignifikant wird. Wird statt eines Tests eine kritische Genauigkeit verwendet, könnte man auch sagen, bis sich die Genauigkeit der Anpassung nicht mehr steigern lässt. Wenn das statistische Material nicht umfangreich genug ist kann es vorkommen, dass die Abhängigkeit der Genauigkeit von der Anzahl der Ansatzfunktionen nicht glatt, sondern rau gegen einen Grenzwert konvergiert – daraus ergeben sich weitere Verbesserungsmöglichkeiten des Verfahrens.
- Bei der rückwärts gerichteten Regression (Backward Regression) werden zunächst alle Regressoren in das Regressionsmodell aufgenommen. Es wird dann der Regressor aus dem Modell entfernt, dessen Weglassen die Quadratsumme der Residuen am wenigsten reduziert. Dann wird der nächste Regressor entfernt usw. Das Verfahren stoppt, wenn der Beitrag des nächsten potentiellen Eliminationskandidaten zur Erklärung von y signifikant hoch wird, bzw. bis die Genauigkeit einen festgelegten Schwellenwert unterschreitet.
- Im allgemeinen ist die Vorwärts-Elimination der Rückwärts-Elimination vorzuziehen, weil die Kreuzproduktmatrix ATA bei sehr vielen Regressoren häufig schon pathologisch ist und für die Eliminationsrechnung keine sinnvollen Ergebnisse liefert.
Auch mit Ridge-Regression kann Multikollinearität abgeholfen werden. Typischerweise sind bei multikollinearen Kreuzproduktmatrizen ATA die Hauptdiagonalelemente zu klein. Man addiert hier iterativ kleine Beträge auf die Hauptdiagonale, bis sich die Matrix stabilisiert hat. Mit Hilfe eines Konditionierungskriteriums, etwa der Eigenwerte, kann dieser Prozess kontrolliert werden. Ob dieses Verfahren sinnvolle Ergebnisse liefert, muss wohl fallweise untersucht werden.
Ausreißer
Als Ausreißer sind Datenwerte definiert, die „untypisch weit von der Masse der Daten entfernt sind“. Diese Werte beeinflussen die Berechnung der Parameter stark. Es gibt hier alternative Ausreißer-resistente Berechnungsverfahren wie gewichtete Regression oder das Drei-Gruppen-Verfahren. Bei der gewichteten Regression werden etwa die Ausreißer der abhängigen Variablen y mit 0 und die unproblematischen Werte mit 1 gewichtet, was die Unterdrückung des Ausreißers bedingt. Dieser Algorithmus nach Mosteller und Tukey (1977) wird als „biweighting“ bezeichnet. Denkbar wäre auch, die Gewichtung je nach Stärke des Ausreißers abzustufen. Im übrigen können auch Ausreißer in den Regressoren die Ergebnisse der Ausgleichsrechnung stark beeinträchtigen. Man spricht hier von Werten mit großer Hebelkraft (High Leverage Value).
 Verschiedene Varianz der Residuen:
Verschiedene Varianz der Residuen:
Die linken Residuen schwanken schwächer als die rechten. Vermutlich sind zwei verschiedene Populationen gemischt worden.Nichtlineare Modellfunktionen
Mit dem Aufkommen leistungsfähiger Rechner gewinnt insbesondere die nichtlineare Regression an Bedeutung. Sie ermöglicht im Prinzip die Anpassung von Daten an jede Gleichung der Form y = f(x). Da diese Gleichungen Kurven definieren, werden die Begriffe nichtlineare Regression und „curve fitting“ zumeist synonym gebraucht.
Manche nichtlineare Probleme lassen sich durch geeignete Substitution in lineare überführen und sich dann wie oben lösen. Ein multiplikatives Modell von der Form
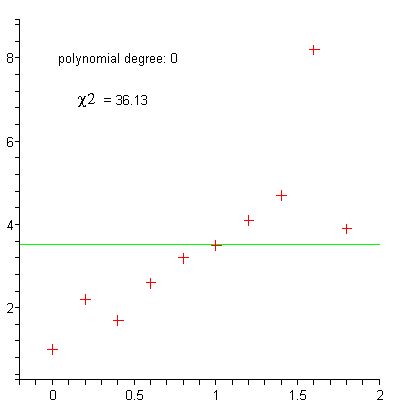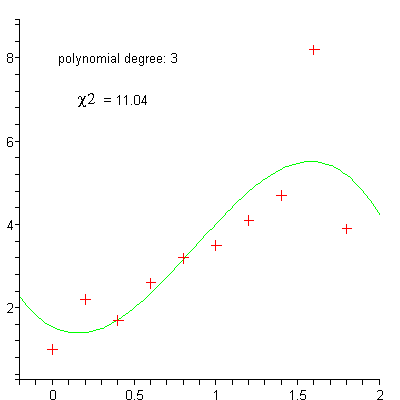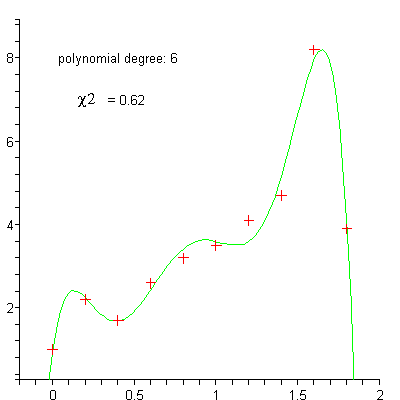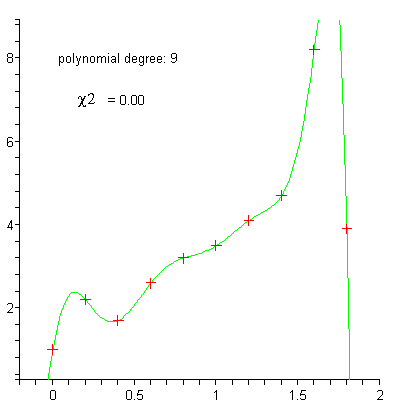
bei dem auch die Residuen e mit t variieren, lässt sich beispielsweise durch Logarithmieren in ein additives System überführen. Dessen Parameter können dann berechnet werden. Dieser Ansatz findet unter Anderem in der Wachstumstheorie Anwendung. Häufig werden für die Approximation einer Funktion y auch Ausgleichspolynome der Form
eingesetzt. Werden für die Potenzen die Zahlenwerte verwendet, ergibt sich wieder ein lineares Gleichungssystem, das wie oben gelöst werden kann.
Im Allgemeinen ergibt sich bei nichtlinearen Modellfunktionen durch die partielle Differentiation ein System von Normalgleichungen, das nicht mehr analytisch gelöst werden kann. Eine numerische Lösung kann hier iterativ mit dem Gauß-Newton-Verfahren erfolgen. Jenes hat das Problem, dass die Konvergenz des Verfahrens nicht gesichert ist.
Aktuelle Programme arbeiten häufig mit einer Variante, dem Levenberg-Marquardt-Algorithmus. Bei diesem Verfahren ist zwar die Konvergenz ebenfalls nicht gesichert, jedoch wird durch eine Regularisierung die Monotonie der Näherungsfolge garantiert. Zudem ist das Verfahren bei größerer Abweichung der Schätzwerte toleranter als die Ursprungsmethode. Beide Verfahren sind mit dem Newton-Verfahren verwandt und konvergieren meist quadratisch, in jedem Schritt verdoppelt sich also die Zahl der korrekten Nachkommastellen.
Wenn die Differenziation auf Grund der Komplexität der Zielfunktion zu aufwändig ist, stehen eine Reihe anderer Verfahren als Ausweichlösung zu Verfügung, die keine Ableitungen benötigen, siehe bei Methoden der lokalen nichtlinearen Optimierung.
Beispiel einer polynomialen Ausgleichskurve
Als Ergebnisse der Mikrozensus-Befragung im Mai 2003 durch das statistische Bundesamt sind die durchschnittlichen Gewichte von Männern nach Altersklassen gegeben (Quelle:© Statistisches Bundesamt, Wiesbaden 2004). Für die Analyse wurden die Altersklassen durch die Klassenmitten ersetzt (Die Zahlen sind im Artikel Streudiagramm aufgeführt). Es soll die Abhängigkeit der Variablen Gewicht (y) von der Variablen Alter (t) analysiert werden.
Das Streudiagramm lässt auf eine annähernd parabolische Beziehung zwischen t und y schließen, welche sich häufig gut durch ein Polynom annähern lässt. Es wird ein polynomialer Ansatz der Form
versucht. Eine Anpassungsrechnung mit Hilfe des Statistik-Programms Minitab ergab die (ins Deutsche übersetzte) Tabelle T1. Es sind alle Parameter xj statistisch signifikant, d.h. die Daten aller t j können einen deutlichen Beitrag zur Erklärung von y leisten. Das Bestimmtheitsmaß (R^2) beträgt 99,8 %, man könnte also sagen, dass 99,8 % der Information von y durch die Daten erklärt werden. Die Daten von t j sind allerdings hochkorreliert. Es wurde daher t 3 und damit der Modellparameter x 3 aus dem Modell entfernt. Die Ergebnisse einer Regression ohne t3 sind in der (ins Deutsch übersetzten) Tabelle T2 aufgeführt. Das Bestimmtheitsmaß ist lediglich auf 98,6 % gesunken, also hat t3 nur einen zusätzlichen Beitrag zur Erklärung von y von 1,3 %. Das Streudiagramm mit den beobachteten und geschätzten y-Werten zeigt, dass die Anpassung gelungen ist.
Beispiel der Fourieranalyse
Auch die Fourieranalyse ist eine Form der Linearisierung einer nichtlinearen Modellfunktion. Die Ansatzfunktionen sind der Kosinus und Sinus der Grundfrequenz und ihrer Vielfachen. Man setzt an
Der mittlere quadratische Fehler wird nach jedem einzelnen Fourierkoeffizienten differenziert, und dieser Ausdruck ist jeweils null:
Daraus ergeben sich die bekannten Definitionsgleichungen der Fourierkoeffizienten.
Beispiel aus der Enzymkinetik einer nicht linearisierbaren Modellfunktion
Ein Beispiel für Regressionsmodelle, die in keiner Weise linearisierbar sind, ist die Enzymkinetik. Hier ist allerdings zu fordern, dass nur y (Reaktionsgeschwindigkeit) und nicht x (Substratkonzentration) einem Fehler unterliegt. Die vertraute Lineweaver-Burk-Beziehung ist zwar eine algebraisch korrekte Umformung der Michaelis-Menten-Gleichung v = Vmax x [S] / (Km + [S]), ihre Anwendung liefert aber nur korrekte Ergebnisse, wenn die Messwerte fehlerfrei sind. Dies ergibt sich aus der Tatsache, dass sich die Realität nur mit einer erweiterten Michaelis-Menten-Beziehung
mit ei als Fehlerparameter, beschreiben lässt. Diese Gleichung lässt sich nicht mehr linearisieren, also muss hier die Lösung iterativ ermittelt werden.
Bei nichtlinearen Gesetzmäßigkeiten ergibt sich eine Komplikation dadurch, dass die zu optimierenden Parameter nicht direkt ermittelt werden können: alle Kalkulationen gehen zwangsläufig von Schätzwerten aus, so dass jede nichtlineare Regressionsanalyse ein iteratives Verfahren darstellt. Ob diese Schätzwerte vernünftig waren, zeigt sich im nachhinein dadurch, dass verschiedene Anfangsschätzungen zum gleichen Endergebnis führen.
Siehe auch
Literatur
- Åke Björk: Numerical Methods for Least Squares Problems. SIAM, Philadelphia 1996, ISBN 0898713609
- Norman R. Draper, Harry Smith: Applied Regression Analysis. Wiley-Interscience, New York 1998, ISBN 0471170828
- Walter Großmann: Grundzüge der Ausgleichsrechnung. Springer Verlag, Berlin Heidelberg New York 1969 (3. erw. Aufl.), ISBN 3540044957
- R. J. Hanson, C. L. Lawson: Solving least squares problems. SIAM, Philadelphia 1995, ISBN 0898713560
- Frederick Mosteller, John W. Tukey: Data Analysis and Regression – a second course in statistics. Addison-Wesley, Reading MA 1977, ISBN 020104854X
- Gerhard Opfer: Numerische Mathematik für Anfänger. Eine Einführung für Mathematiker, Ingenieure und Informatiker. Vieweg, Braunschweig 2002 (4. Aufl.), ISBN 3528372656
- Volker Oppitz, Volker Nollau: Taschenbuch Wirtschaftlichkeitsrechnung. Carl Hanser, München 2003, ISBN 3446224637
- Volker Oppitz: Gabler Lexikon Wirtschaftlichkeitsberechnung. Gabler, Wiesbaden 1995, ISBN 3409199519
- Josef Schira: Statistische Methoden der VWL und BWL. Pearson Studium, München 2003, ISBN 3827370418
- Peter Schönfeld: Methoden der Ökonometrie. 2 Bd. Vahlen, Berlin-Frankfurt 1969-1971.
- E. Zeidler (Hrsg.): Taschenbuch der Mathematik. Begründet v. I.N. Bronstein, K.A. Semendjajew. Teubner, Stuttgart-Leipzig-Wiesbaden 2003, ISBN 3817120052
Weblinks
Frei verfügbare Implementierungen des Levenberg-Marquardt-Algorithmus finden sich unter
Wikimedia Foundation.

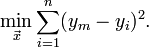
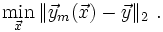
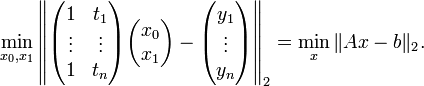
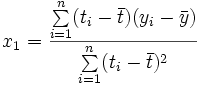
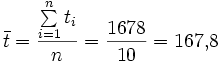
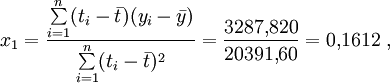
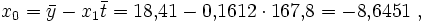
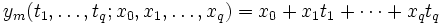
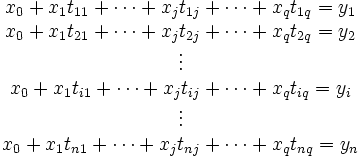
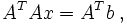


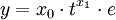
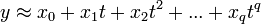

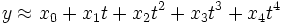



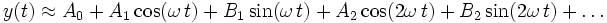
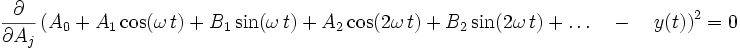
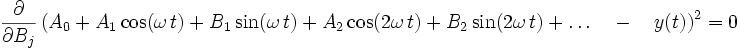
![\nu_i = \frac{V_\max\left[S_i\right]}{K_m+\left[S_i\right]}(1+e_i)\ \boldsymbol{\nu}_i](/pictures/dewiki/57/99eff93c53043ccd425abe32012a047a.png)