Leeres Wort

Das leere Wort ist in der Theoretischen Informatik und in der Praktischen Informatik ein Wort, das aus keinem einzigen Zeichen besteht, also die Länge 0 hat. Es wird auch Leerstring genannt. In vielen Programmiersprachen wird ein solcher String durch ein Literal dargestellt, bei dem die beiden Anfangs- und Endzeichen, die eine Zeichenkette einschließen, unmittelbar aufeinander folgen, z. B. "" in Perl oder Java.

Definition

Das leere Wort über dem Alphabet Σ ist eine Folge von Elementen aus Σ der Länge 0.

Schreibweise

Das leere Wort wird meist mit dem griechischen Buchstaben ε (Epsilon für Englisch „empty“) dargestellt, oft findet sich dafür aber auch der griechische Buchstabe λ (Lambda, vom Deutschen „leer“). Andere übliche Darstellungen sind $\epsilon$ als andere Schreibweise des Epsilon, e (ebenfalls für „empty“) und 1 als Einselement eines multiplikativ geschriebenen Monoids.

Merkmale

• | ε | = 0

Die Länge des leeren Wortes ist stets 0. Diese Eigenschaft folgt direkt aus der Definition.

• $\forall w \in \Sigma^*: \varepsilon w = w \varepsilon = w$

Das leere Wort bildet bei der Konkatenation von Wörtern das neutrale Element, sprich, die Verkettung eines beliebigen Wortes w über ein beliebiges Alphabet Σ mit ε ergibt stets wieder w.

• $\varepsilon \in \Sigma^*$

Das leere Wort ε ist Element der Kleeneschen Hülle über jedes beliebige Alphabet Σ. Anders ausgedrückt ist das leere Wort in der Menge aller Wörter über Σ.

• ε^R = ε

Das leere Wort ist identisch mit seiner Spiegelung und damit ein Palindrom.

Weitere Merkmale bei speziellen Anwendungen

Ein Automat, der das leere Wort unter Verwendung einer ε-Transition akzeptiert

[ε] = L: Betrachtet man die Äquivalenzklassen einer formalen Sprache L bezüglich der Nerode-Relation ~, so bildet ε stets eine Äquivalenzklasse, die exakt L entspricht. Demnach beträgt der Index von L bezüglich ~ stets mindestens 1, in Zeichen ind(L) > = 1. Daraus wiederum lässt sich folgern, dass ein Deterministischer endlicher Automat, der L akzeptiert, aus mindestens einem Zustand bestehen muss.

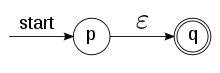
ε-Übergänge in Nichtdeterministischen endlichen Automaten sind Tupel (q₁,ε,q₂) aus der Übergangsrelation Δ mit Zuständen q₁,q₂. Ein solcher Übergang bedeutet, dass der Automat seinen Zustand von q₁ nach q₂ ändern kann, ohne dass ein Zeichen gelesen wird. ε-Übergänge sind damit einer der Gründe für Nichtdeterminismus. Sie werden im Graphen als Kanten kenntlich gemacht, die mit einem ε beschriftet sind.

Literatur

• John E. Hopcroft, Jeffrey D. Ullman: Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie. 2. Auflage. Pearson Studium, Reading 2002, ISBN 3-8273-7020-5

Weblinks

 Wiktionary: leeres Wort – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen