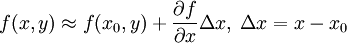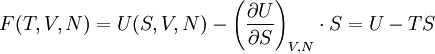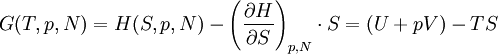Legendretransformation

Anschauliche Darstellung der Legendre-Transformation

Die Legendre-Transformation (nach Adrien-Marie Legendre) gehört zu den Berührungstransformationen und dient als wichtiges mathematisches Verfahren zur Variablentransformation.

Ziel der Legendre-Transformation ist die Änderung der Abhängigkeit einer Funktion f(x) von einer Variablen x zu einer anderen Variablen u, für die gilt

$u=\frac{\partial f}{\partial x}$.

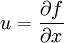Wenn man für die von x abhängige Funktion f(x) schreiben kann

$\mathrm{d}f=\frac{\partial f}{\partial x}\,\mathrm{d}x=u\,\mathrm{d}x$,

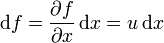dann soll für die von u abhängige Funktion g(u) auch gelten:

$\mathrm{d}g=\pm x\,\mathrm{d}u$.

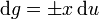Bilden wir zunächst das totale Differential von 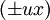$(\pm ux)$, so erhalten wir

$\mathrm{d}(\pm ux)=\pm(x\,\mathrm{d}u+u\,\mathrm{d}x)$.

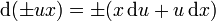Der Vergleich mit df und dg liefert uns

$\mathrm{d}(\pm ux)=\mathrm{d}g \pm u\,\mathrm{d}x = \mathrm{d}g \pm \mathrm{d}f$.

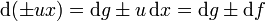Daraus schließen wir

$\mathrm{d}g=\mathrm{d}(\mp f\pm ux)$,

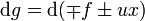Nach einer Integration gilt also

$g(u)=\pm(-f(x(u))+ux(u))$.

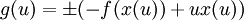Die Funktion g(u) wird als Legendre-Transformierte von f bezeichnet. Das Vorzeichen von g ist für die Definition unwichtig, wir können also g = ux − f oder g = f − ux schreiben. Welches Vorzeichen man wählen sollte, hängt von der physikalischen Bedeutung von g ab.

Geometrische Bedeutung der Legendre-Transformation

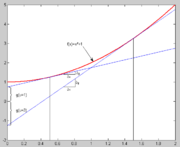
Geometrisch lässt sich der Sachverhalt wie in Abbildung 1 veranschaulichen: Die Kurve (rot) kann, statt die Punktmenge anzugeben, aus der sie besteht, auch durch die Menge aller Tangenten charakterisiert werden, die sie einhüllen. Genau das passiert bei der Legendre-Transformation. Die Transformierte, g(u), ordnet der Steigung u einer jeden Tangente deren Y-Achsenabschnitt zu. Es ist also eine Beschreibung derselben Kurve - nur über einen anderen Parameter, nämlich u statt x.

Bei Abhängigkeit von mehreren Variablen

Die Änderung der Abhängigkeit einer Funktion f(x,y) von einer unabhängigen Variablen x zu einer anderen u mittels einer partiellen Ableitung von f nach x ist:

$u = \frac{\partial f}{\partial x}$.

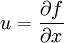Hierbei stellt u(x,y) geometrisch die Steigung in x-Richtung der Tangentenebene an die Funktion f(x,y) dar. Daher spricht man von Berührungstransformation. Die Funktion F(u,y) wird als Legendre-Transformierte bezeichnet.

Die Legendre-Transformierte lässt sich wie folgt herleiten. Der Wert von f(x,y) kann alternativ als

$f(x,y) \approx f(x_0,y)+\frac{\partial f} {\partial x} \Delta x,\; \Delta x = x-x_0$

geschrieben werden. Definiert man nun 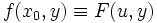$f(x_0,y) \equiv F(u,y)$, erhält man für die Legendre-Transformierte

$F(u,y) = f(x,y)-\frac{\partial f}{\partial x} \Delta x$.

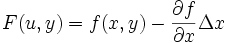Meistens wird x₀ = 0 gewählt, und somit folgt

$F(u,y) = f(x,y)-\frac{\partial f}{\partial x} x$.

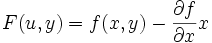Für letztere Definition ist die Legendre-Transformierte die y-Komponente des Schnittpunkts der Tangentenebene an f(x,y) mit der Ebene x = 0. Für Funktionen in der Ebene spricht man vom Achsenabschnitt (siehe auch Geradengleichung).

Praktisch erfolgt also der Austausch der unabhängigen Variablen durch Subtraktion des Produkts aus alter und neuer Variable ux von der Ausgangsfunktion:

F(u,y) = f(x,y) − ux.

Dies wird auch bei Betrachtung des totalen Differentials der Legendre-Transformierten deutlich:

$\mathrm{d}(f(x,y) - u x) = \mathrm{d}f(x,y) - x\,\mathrm{d}u - u\,\mathrm{d}x = \frac{\partial f} {\partial x} \mathrm{d}x + \frac{\partial f} {\partial y} \mathrm{d}y - x \mathrm{d}u - u \mathrm{d}x = \frac{\partial f} {\partial y} \mathrm{d}y - x\,\mathrm{d}u = \mathrm{d}F(u,y)$.

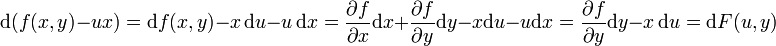Anwendungsgebiete

Verwendung in der Physik findet die Legendre-Transformation vor allem in der (statistischen) Thermodynamik (z. B. Umwandlung der Fundamentalgleichung bzw. beim Übergang zwischen thermodynamischen Potentialen unter verschiedenen Randbedingungen) und beim Übergang von der Lagrangeschen zur Hamiltonschen Mechanik (Lagrange-Funktion zu Hamilton-Funktion).

Die Legendre-Transformation spielt - wie die Berührungstransformationen insgesamt - des Weiteren eine Rolle in der Mechanik, der Variationsrechnung und in der Theorie der partiellen Differentialgleichungen 1. Ordnung.

Beispiele

In der Thermodynamik kann man durch Legendre-Transformation aus der Fundamentalgleichung der Thermodynamik die thermodynamischen Potentiale ableiten. Dabei findet beispielsweise ein Übergang von der inneren Energie U (abhängig von der Entropie S) zur Helmholtz-Energie F (abhängig von der Temperatur T) statt:

$F(T,V,N) = U(S,V,N) - \left(\frac{\partial U}{\partial S}\right)_{V,N} \cdot S = U - T S$

Die hier verwendete Ableitungsnotation bedeutet Ableitung der Funktion U(S,V,N) nach S, wobei V und N konstant gehalten werden.

Analog dazu ist auch ein Übergang von einem thermodynamischen Potential zu einem anderen möglich, beispielsweise von der Enthalpie H zur Gibbs-Energie G:

$G(T,p,N) = H(S,p,N) - \left(\frac{\partial H}{\partial S}\right)_{p,N} \cdot S = (U + p V) - T S$

Auf die gleiche Weise erhält man auch die anderen thermodynamischen Potentiale, wobei durch eine Legendre-Transformation immer eine generalisierte Koordinate durch die konjugierte thermodynamische Kraft ersetzt wird.