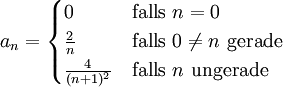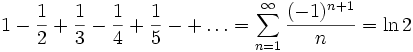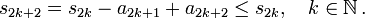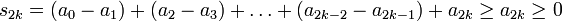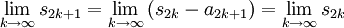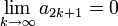Leibnizsches Konvergenzkriterium

Das Leibniz-Kriterium (nach Gottfried Wilhelm Leibniz) ist ein mathematisches Konvergenzkriterium, also Mittel zur Entscheidung, ob eine unendliche Reihe konvergiert.

Definition

Eine alternierende Reihe

Sei (a_n) mit 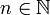$n \in \mathbb{N}$ eine monoton fallende, reelle Nullfolge mit 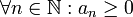$\forall n \in \mathbb{N}: a_n \geq 0$, dann konvergiert die unendliche alternierende Reihe.

$s = \sum_{n=0}^\infty (-1)^n a_n \,$.

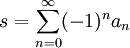Beachte: Es genügt nicht, dass (a_n) nur eine Nullfolge ist, die Monotonie ist notwendig für dieses Kriterium. Betrachte z.B. dieses Gegenbeispiel:

$a_n = \begin{cases} 0 & \mathrm{falls}\ n=0 \\ \frac{2}{n} & \mathrm{falls}\ 0\ne n\ \mathrm{gerade}\\ \frac{4}{(n+1)^2} & \mathrm{falls}\ n\ \mathrm{ungerade} \end{cases} \,$

Die Reihe S mit diesen Koeffizienten hat als positive Terme die harmonische Reihe, die divergiert, und als negative Terme die Reihe der reziproken Quadrate, die konvergiert. Insgesamt ist diese Reihe also divergent.

Das Leibniz-Kriterium liefert eine Abschätzung für den Grenzwert, denn bei derartig alternierenden Reihen liegt der Grenzwert immer zwischen zwei aufeinanderfolgenden Partialsummen. Sei s_k die k-te Partialsumme der Folge,

$s_k = \sum_{n=0}^k (-1)^n a_n \,$.

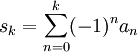Dann gilt für alle $l \in \mathbb{N}$:

$s_{2l-1} \le s \le s_{2l} \,$.

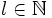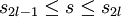Es gibt zudem noch eine Fehlerabschätzung, d.h. eine Abschätzung des Restglieds der Summe nach N Summanden:

$|S-S_N| = |\sum_{n=N+1}^\infty (-1)^n a_n| \le a_{N+1} \,$.

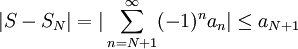Beispiele

Häufig genannte Beispiele von Reihen, deren Konvergenz mit dem Leibniz-Kriterium gezeigt werden kann, sind etwa die alternierende harmonische Reihe

$1-\frac12+\frac13-\frac14+\frac15-+\dots=\sum_{n = 1}^\infty \frac{(-1)^{n + 1}}{n} = \ln 2$

sowie die Leibniz-Reihe

$1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \dots = \sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1} = \frac{\pi}{4}$.

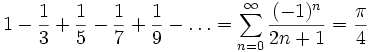Man beachte, dass sich aus dem Leibniz-Kriterium nur ergibt, dass diese Reihen konvergieren, über den genauen Grenzwert macht es keine Aussagen.

Beweis

Wir betrachten die Teilfolge 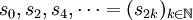$s_0,s_2,s_4,\dots = (s_{2k})_{k\in\mathbb{N}}$ der Folge der Partialsummen. Da die Beträge der Glieder a_i monoton abnehmen, gilt

$s_{2k+2}=s_{2k}-a_{2k+1}+a_{2k+2}\le s_{2k},\quad k\in\mathbb{N}\,.$

d.h. die Folge (s_2k)_k ist monoton fallend. Sie ist außerdem nach unten beschränkt, denn

$s_{2k}=(a_0-a_1)+(a_2-a_3)+ \dots +(a_{2k-2}-a_{2k-1})+a_{2k}\ge a_{2k} \ge 0$

wobei die Klammerausdrücke wegen der Monotonie der Beträge der Glieder a_i größer gleich Null sind. Die Folge (s_2k)_k ist also nicht nur monoton fallend sondern auch nach unten beschränkt und damit konvergent. Die Folge 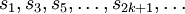$s_1,s_3,s_5,\dots,s_{2k+1},\dots$ ist ebenfalls konvergent (ähnliches Argument wie oben, aber monoton steigend) und hat denselben Grenzwert, da

$\lim_{k\rightarrow\infty} s_{2k+1}= \lim_{k\rightarrow\infty} \left(s_{2k} - a_{2k+1}\right) =\lim_{k\rightarrow\infty} s_{2k}$

wegen

$\lim_{k\rightarrow\infty}a_{2k+1}=0$

gilt. ^[1]

Weblinks

• Beweis: Leibniz-Kriterium

Einzelnachweise

1. ↑ Beweis nach Handbuch der Mathematik Leipzig 1986 ISBN 3-8166-0015-8 Seite 408-409 - im Unterschied zu diesem Artikel beginnt die Reihe im Buch mit a_1, so dass sich ein kleiner Unterschied ergibt.