Lexikographisch

Die lexikographische Ordnung ist in der Informatik und Mathematik eine Methode, um aus einer linearen Ordnung für einfache Objekte (beispielsweise Buchstaben angeordnet nach dem Alphabet) eine lineare Ordnung für zusammengesetzte Objekte (beispielsweise Wörter) zu erhalten. Das namengebende Beispiel ist die Anordnung der Wörter in einem Lexikon: Sie werden zunächst nach ihren Anfangsbuchstaben sortiert, dann die Wörter mit gleichen Anfangsbuchstaben nach dem jeweils zweiten Buchstaben usw. Ist ein Wort ganz in einem anderen als Anfangsteil enthalten (wie beispielsweise „Tal“ in „Talent“), so wird das kürzere Wort zuerst aufgeführt.

Formal kann diese Ordnung wie folgt beschrieben werden: Eine Zeichenkette a ist kleiner als eine Zeichenkette b (d. h. a liegt in der Sortierung vor b), wenn

• entweder das erste Zeichen von a, in dem sich beide Zeichenketten unterscheiden, kleiner ist als das entsprechende Zeichen von b,
• oder wenn a den Anfang von b bildet, aber kürzer ist.

Ein Spezialfall dieser Ordnung ist die lexikographische Ordnung von endlichen Folgen einer festen Länge verwendet. Beispielsweise bei Paaren ist ein Paar (a₁,a₂) lexikographisch kleiner als ein Paar (b₁,b₂), wenn

• entweder a₁ < b₁
• oder a₁ = b₁ und a₂ < b₂

gilt.

Ein Beispiel für eine derartige Ordnung ist die zeitliche Reihenfolge für Zahlentripel (Jahr, Monat, Tag): Ein Datum X ist früher als ein anderes Datum Y, wenn

• entweder die Jahreszahl von X kleiner ist als die Jahreszahl von Y
• oder die Jahreszahlen gleich sind, aber X in einem im Jahresverlauf früheren Monat liegt
• oder die Jahreszahlen und Monate gleich sind, aber der Tag von X kleiner als der Tag von Y ist.

Ein weiteres Beispiel ist die übliche Rangfolge innerhalb eines Medaillenspiegels, bei der als erstes Kriterium die Anzahl der Goldmedaillen ausschlaggebend ist, bei gleicher Goldmedaillenzahl die Anzahl der Silbermedaillen und bei nochmaligem Gleichstand die Anzahl der Bronzemedaillen.

Mathematische Verwendung

Analog lässt sich die lexikographische Ordnung auch auf unendlichen Folgen definieren: Eine Folge 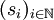$(s_i)_{i\in\mathbb{N}}$ ist lexikographisch kleiner als eine Folge 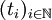$(t_i)_{i\in\mathbb{N}}$ wenn beide Folgen vor einem bestimmten Index k gleich sind aber s_k < t_k. Das Prinzip kann ausgedehnt werden auf Folgen, in denen der Indexbereich eine beliebige wohlgeordnete Menge W ist. In diesem Fall definiert man f<g für Funktionen f,g: W→X (wobei X linear geordnet ist) als: Für das minimale Element w der Index-/Argumentmenge, auf der sich f und g unterscheiden, gilt: f(w)<g(w). Die so entstandene Ordnung auf den Funktionen ist wieder linear.

Das lexikographische Prinzip kann auch angewendet werden, wenn die zusammengesetzten Objekte endliche Mengen oder endliche Multimengen (statt nur endliche Folgen bzw. Zeichenketten) sind. Dazu ordnet man in jeder (Multi)Menge die Elemente vom größten zum kleinsten und vergleicht die entstandenen endlichen Folgen lexikographisch. Diese Anordnung wird entgegengesetzt lexikographische Ordnung genannt (wohl weil natürlicherweise die gebildeten Folgen aufsteigend wären, und die lexikographische Ordnung von absteigenden Folgen, der entgegengesetzt (also von rechts nach links ausgeführten) lexikographischen Ordnung der entsprechenden aufsteigenden Folgen entspricht). Sie ist ebenfalls eine lineare Ordnung der zusammengesetzten Objekte.