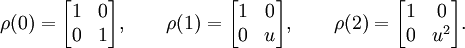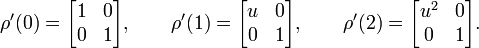Lineare Darstellung

Die hier beschriebene Darstellungstheorie ist ein Teilgebiet der Mathematik, das auf der Gruppentheorie aufbaut und ein Spezialfall der eigentlichen Darstellungstheorie ist, welche sich mit Darstellungen von Algebren beschäftigt.

Die Grundidee ist, die Elemente einer Gruppe durch Transformationen bestimmter mathematischer Objekte darzustellen.

Eine Darstellung ρ einer Gruppe G ist ein Homomorphismus von G in die Automorphismengruppe Aut(W) einer gegebenen Struktur W. Die Gruppenverknüpfung in G entspricht dem Hintereinanderausführen von Automorphismen in W: ρ(gh)=ρ(g) ρ(h).

Eine lineare Darstellung ist eine Darstellung durch Automorphismen eines Vektorraums V. Eine lineare Darstellung ist somit ein Homomorphismus von G in die allgemeine lineare Gruppe GL(V). Wenn V ein n-dimensionaler Vektorraum über einem Körper K ist, dann besteht die Darstellung dementsprechend aus invertierbaren n×n-Matrizen mit Koeffizienten aus K. Die Vektorraumdimension n heißt Grad der Darstellung.

Oft wird der Begriff Darstellung im engeren Sinn von lineare Darstellung verwandt; eine Darstellung durch beliebige Automorphismen heißt dann Realisierung.

Glossar

• Eine Darstellung heißt treu, wenn der Darstellungshomomorphismus injektiv ist, wenn also verschiedene Gruppenelemente stets durch verschiedene Transformationen dargestellt werden.

• Die triviale Darstellung 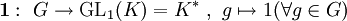$\mathbf{1}: \ G \rightarrow \operatorname{GL}_1(K)=K^* \ , \ g \mapsto 1 (\forall g \in G)$ ist im Allgemeinen nicht treu.

• Zwei lineare Darstellungen ρ₁, ρ₂ heißen äquivalent, wenn ihre Matrizen ähnlich sind, also die gleiche lineare Abbildung für unterschiedliche Basen darstellen. D.h., wenn es eine invertierbare Matrix S gibt, so dass für alle Gruppenelemente g gilt: ρ₁(g) = S ρ₂(g) S^-1.

• Tritt in einem Kontext nur eine Darstellung ρ auf, so schreibt man statt ρ(g)(v) oft nur gv.

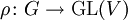• Sei V ein $\mathbb{C}$-Vektorraum. Die Darstellung $\rho \colon G \rightarrow \operatorname{GL}(V)$ heißt unitär, wenn auf V eine G-invariante, positiv definite Norm 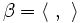$\beta = \langle \ , \ \rangle$ existiert, d.h., wenn für β gilt: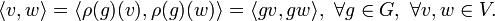 $\langle v,w \rangle = \langle \rho(g)(v),\rho(g)(w) \rangle = \langle gv,gw \rangle , \ \forall g\in G,\ \forall v,w \in V .$

• Sei 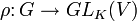$\rho \colon G \rightarrow GL_K(V)$ eine Darstellung der Gruppe G auf dem K-Vektorraum V. Ein Unterraum 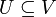$U \subseteq V$ heißt G-invariant (genauer: ρ-invariant), falls gilt: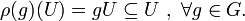 $\rho(g)(U)=gU \subseteq U \ , \ \forall g \in G.$

• Die Darstellung ρ (bzw. der Darstellungsraum V) heißt irreduzibel, falls es nur die beiden trivialen G-invarianten Unterräume 0( = {0}) und 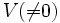$V(\not= 0)$ von V gibt. (Eine Hauptaufgabe der Darstellungstheorie ist die Klassifikation irreduzibler Darstellungen.) Insbesondere im nicht-halbeinfachen Fall und in der Betrachtungsweise als Moduln werden solche Darstellungen auch einfach genannt.
• Ist ρ nicht irreduzibel, so heißt ρ reduzibel.
• Ist ρ eine direkte Summe von irreduziblen Darstellungen von G, so heißt ρ vollständig reduzibel. Insbesondere ist jede irreduzible Darstellung vollständig reduzibel.
• Lässt sich ρ nicht in eine nichttriviale direkte Summe von (nicht notwendigerweise irreduziblen) Darstellungen zerlegen, so heißt ρ unzerlegbar, ansonsten zerlegbar. (Man beachte, dass nur im Fall 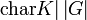$\operatorname{char}K | \left| G \right|$ irreduzibel und unzerlegbar nach dem Satz von Maschke identisch sind.)

• Ist 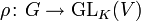$\rho \colon G \rightarrow \operatorname{GL}_K(V)$ eine Darstellung, dann bezeichnet man als Zentrum Z(ρ) von ρ die Menge der KG-Endomorphismen von V, also:

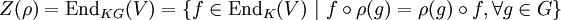$Z(\rho)=\operatorname{End}_{KG}(V)=\{f \in \operatorname{End}_K(V)\ | \ f \circ \rho (g) = \rho (g) \circ f , \forall g \in G \}$. Ist ρ eine Matrixdarstellung, also 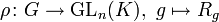$\rho \colon G \rightarrow \operatorname{GL}_n(K), \ g \mapsto R_g$, dann gilt: 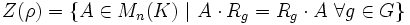$Z(\rho)=\{A \in M_n(K) \ | \ A \cdot R_g=R_g \cdot A \ \forall g \in G \}$. Nach dem Lemma von Schur ist das Zentrum für irreduzible Darstellungen ein Schiefkörper. Die Umkehrung gilt auch, so dass Z(ρ) genau dann ein Schiefkörper ist, wenn ρ irreduzibel ist.

Anwendungen

Lineare Darstellungen ermöglichen es, Eigenschaften einer Gruppe mit den Mitteln der linearen Algebra zu untersuchen; das ist nützlich, weil die lineare Algebra, im Gegensatz zur Gruppentheorie, ein kleines, abgeschlossenes und bestens verstandenes Gebiet ist.

Darstellungen endlicher Gruppen ermöglichen es in der Molekülphysik und Kristallographie, die Auswirkungen vorhandener Symmetrien auf messbare Eigenschaften eines Materials mit Hilfe eines rezeptmäßigen Kalküls zu bestimmen.

Beispiel

Sei G die zyklische Gruppe C₃, also die Menge {0,1,2} mit der Addition modulo 3 als Gruppenverknüpfung.

Die Abbildung τ: G→C, die den Gruppenelementen g Potenzen τ(g) = u^g der komplexen Zahl u = exp(2πi/3) zuordnet, ist eine treue lineare Darstellung vom Grad 1. Der Gruppeneigenschaft g³ = e entspricht die Eigenschaft u³ = 1. Die durch die Darstellung erzeugte multiplikative Gruppe τ(C₃) = {1, u, u²} ist isomorph zur dargestellten Gruppe C₃.

Eine solche Isomorphie liegt ebenfalls vor bei der treuen linearen Darstellung vom Grad 2, die gegeben ist als

$\rho(0)=\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}, \qquad \rho(1)=\begin{bmatrix} 1 & 0 \\ 0 & u \\ \end{bmatrix}, \qquad \rho(2)=\begin{bmatrix} 1 & 0 \\ 0 & u^2 \\ \end{bmatrix}.$

Diese Darstellung ist äquivalent zu einer Darstellung durch die folgenden Matrizen:

$\rho'(0)= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}, \qquad \rho'(1)= \begin{bmatrix} u & 0 \\ 0 & 1 \\ \end{bmatrix}, \qquad \rho'(2)= \begin{bmatrix} u^2 & 0 \\ 0 & 1 \\ \end{bmatrix}.$

Die Darstellungen ρ und ρ´ sind reduzibel: sie bestehen aus der direkten Summe der zuvor beschriebenen Darstellung g→u^g und der untreuen Darstellung g→1.

Charakter

Hauptartikel: Charakter (Mathematik)

Der Charakter der endlichdimensionalen Darstellung 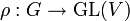$\rho: G\to \mathrm{GL}(V)$ ist die Funktion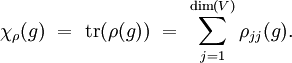

$\chi_{\rho}(g) \ =\ \operatorname{tr}(\rho(g))\ =\ \sum_{j=1}^{\dim(V)}\rho_{jj}(g).$

Dabei sind ρ_jj die Matrixelemente in einer beliebigen Basis von V. Die sogenannte Spur tr ist basisunabhängig. Es gelten folgende Eigenschaften:

• ρ und ρ' sind äquivalent, falls χ_ρ = χ_ρ'
• χ(g) = χ(hgh ^{− 1}) weil tr(AB) = tr(BA). Deshalb ist χ auf den Konjugationsklassen konstant.
• χ(1_G) = dim(V), direkt aus Spur ersichtlich
• $\chi_{\rho\oplus \rho'}= \chi_\rho + \chi_{\rho'}$

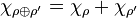
Damit kann man testen, ob eine Darstellung irreduzibel ist 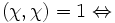$(\chi,\chi)=1 \Leftrightarrow$ irred., ob Darstellungen äquivalent sind usw.

Vollständig reduzible Darstellungen endlicher Gruppen zerfallen in irreduzible Darstellungen. Damit kann man die Darstellungen aus den Charakteren erschließen. Man kann die Charaktertafel einer Darstellung aufstellen.

Literatur dazu unter http://www-ifm.math.uni-hannover.de/~bothmer/Darstellungstheorie/charaktere.pdf

Taxonomie

Darstellungen können nach zwei Gesichtspunkten klassifiziert werden: (1) nach der Struktur der Zielmenge W, auf die die Darstellungen wirken; und (2) nach der Struktur der dargestellten Gruppe.

Einteilung nach Zielmengen

Eine mengentheoretische Darstellung ist ein Homomorphismus der darzustellenden Gruppe auf die Permutationsgruppe Sym(M) einer beliebigen Menge M; siehe dazu auch den Satz von Cayley.

Eine lineare Darstellung ist durch ihre Dimension n und durch den Körper K charakterisiert. Neben den komplexen und reellen Zahlen kommen hier die endlichen und p-adischen Körper in Betracht.

Eine modulare Darstellung ist eine Darstellung über einem endlichen Körper; wichtige Ergebnisse hängen von der Charakteristik des Körpers ab.

Darstellungen in Untergruppen der allgemeinen linearen Gruppe GL(V) zeichnen sich dadurch aus, dass sie gewisse Strukturen des Vektorraums V erhalten. Zum Beispiel erhält eine unitäre Darstellung, also eine Darstellung in die unitäre Gruppe U(V), das Skalarprodukt.

Einteilung nach dargestellter Gruppe

Einfachster Fall ist die Darstellung einer endlichen Gruppe.

Viele Ergebnisse in der Darstellungstheorie endlicher Gruppen werden durch Mittelung über die Gruppe erzielt. Diese Ergebnisse können auf unendliche Gruppen übertragen werden, sofern die topologischen Voraussetzungen gegeben sind, um ein Integral zu definieren. Dies ist vermittels des Haar-Maßes in lokal kompakten Gruppen möglich. Die daraus resultierende Theorie spielt eine zentrale Rolle in der harmonischen Analyse. Die Pontrjagin-Dualität beschreibt diese Theorie im Spezialfall abelscher Gruppen als verallgemeinerte Fourier-Transformation.

Viele wichtige Lie-Gruppen sind kompakt, so dass die genannten Ergebnisse übertragbar sind; die Darstellungstheorie ist von entscheidender Bedeutung für die Anwendungen dieser Lie-Gruppen in Physik und Chemie.

Für nicht-kompakte Gruppen gibt es keine abgeschlossene Darstellungstheorie. Eine umfassende Theorie ist für halb-einfache Lie-Gruppen ausgearbeitet worden. Für die komplementären auflösbaren Lie-Gruppen gibt es keine vergleichbare Klassifikation.

Literatur

• Sommersemester 2002, F.G. Timmesfeld, Universität Gießen http://www.uni-giessen.de/AG_Algebra/DarstTh-SS2002/main.pdf (viele Beispiele mit Charaktertafeln)
• Vorlesung von G. Felder an der ETH http://www.math.ethz.ch/~felder/mmp/mmp2/
• Skripten von W. Soergel an der Uni Freiburg http://home.mathematik.uni-freiburg.de/soergel/#Skripten