Linienintensität

Als Spektrallinien bezeichnet man voneinander scharf getrennte Linien eines Spektrums emittierter (Emissionslinien) oder absorbierter (Absorptionslinien) elektromagnetischer Wellen, im engeren Sinne innerhalb des Wellenlängenbereichs des sichtbaren Lichts (Lichtspektrum). Spektrallinien werden durch Wellenlänge, Linienintensität und Linienbreite charakterisiert.

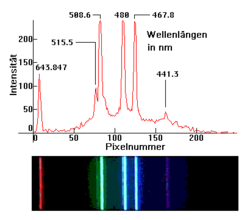Spektrum einer Niederdruck-Cadmiumdampflampe. Obere Aufnahme mit einem 256-Pixel-Zeilensensor. Untere Aufnahme mit einer Kamera

Grundlagen

Eine Spektrallinie ist das Licht einer genau definierten Frequenz, das von einem Atom oder Molekül aufgrund eines quantenmechanischen Übergangs abgegeben oder absorbiert wird. Es dient der Unterscheidung unterschiedlicher Atomsorten. Angewandt wird dies bei der instrumentellen Atomspektroskopie oder der Flammenfärbung.

Die Frequenz einer Spektrallinie wird durch die Energie des emittierten oder absorbierten Photons bestimmt, die gerade den Unterschied zwischen den Energien der quantenmechanischen Zustände bestimmt.

Erstmals entdeckt wurden Absorptionslinien 1802 durch William Hyde Wollaston und 1813, unabhängig von ihm, durch Joseph von Fraunhofer im Spektrum der Sonne. Diese dunklen Linien im Sonnenspektrum werden auch Fraunhofersche Linien genannt.

Die Emissionslinien

Kontinuierliches Lichtspektrum ohne Spektrallinien

Emissionslinien

Eine Emissionslinie ergibt sich durch Übergang von einem höheren auf ein tieferes Energieniveau. Hierbei wird ein Photon ausgesendet. Dies kann entweder spontan geschehen (spontane Emission), oder, wie beispielsweise beim Laser, durch Licht passender Frequenz angeregt werden (stimulierte Emission). Sie zeigt sich im Spektrum als helle Linie.

Die Absorptionslinien

Absorptionslinien

Eine Absorptionslinie ergibt sich durch Resonanzabsorption eines passenden Photons des eintreffenden Lichts, wodurch ein Übergang von einem niedrigeren in ein höheres Energieniveau induziert wird. Beim Rückfall in das niedrigere Energieniveau werden Photonen isotrop in beliebige Richtungen emittiert, so dass (wenn ausreichend viele absorbierenden Atome vorhanden sind)

• eine dunkle Linie im kontinuierlichen Spektrum des durchscheinenden Lichts zu beobachten ist (Fraunhoferlinien).
• eine helle Emissionslinie vor dunklem Hintergrund zu sehen ist, wenn man das vom Gas seitlich austretende Licht analysiert.

Emissionsprofile

Das Licht einer Spektrallinie enthält nicht eine Frequenz, sondern einen (schmalen) Frequenzbereich. Die Breite dieses Bereiches nennt man Linienbreite. Die Linienbreite einer Emissionslinie setzt sich aus mehreren Beiträgen zusammen:

• Lorentz-Profil: Die natürliche Linienbreite ergibt sich aus der Lebensdauer des Ausgangszustands durch die heisenbergsche Unschärferelation. Diese hat die Form einer Lorentz-Kurve. Es ist nicht möglich, diese zu verringern.
• Gauß-Profil: Aufgrund der thermischen Bewegung der Atome entsteht ein Doppler-Effekt, der das Licht eines einzelnen Atoms oder Moleküls je nach Bewegungsrichtung rot- oder blauverschiebt. Aufgrund der statistischen Bewegung ergibt sich insgesamt eine breitere Frequenzverteilung. Diesen Effekt nennt man Doppler-Verbreiterung. Sie hat die Form einer Gauß-Kurve und ist abhängig von der Temperatur. Meist dominiert die Dopplerbreite deutlich über die natürliche Linienbreite. Der Mechanismus ist auch unter dem Begriff inhomogene Linienverbreiterung bekannt.
• Voigt-Profil: Eine Lorentz-Kurve endlicher Breite erscheint bei einer Messung gegenüber seiner bekannten Form verändert, wenn die Apparatefunktion der Messanordnung eine Halbwertsbreite in der Größenordnung der betrachteten Lorentz-Kurve aufweist. Die Linienform lässt sich dann durch die Faltung aus Lorentz-Kurve und Apparatefunktion beschreiben. Folgt letztere einer Gauß-Kurve, spricht man bei dem Ergebnis der Faltung von einem Voigt-Profil

Spektren und Quantenmechanik

Die Spektrallinien waren einer der Effekte, die zur Entwicklung der Quantenmechanik beitrugen. Ein in einem Atom gebundenes Elektron könnte nach der klassischen Elektrodynamik elektromagnetische Wellen beliebiger Frequenzen abstrahlen; die Existenz von diskreten Linien war klassisch nicht erklärbar. Die Entdeckung, dass die Frequenzen der Spektrallinien des Wasserstoffatoms proportional zu einem Ausdruck der Form (1/n² - 1/m²) mit ganzen Zahlen m und n sind, führte zum Konzept der Quantenzahl und brachte Niels Bohr schließlich auf sein Bohrsches Atommodell, das erste - heute überholte - quantenmechanische Atommodell. Die moderne Quantenmechanik kann die Spektrallinien der Atome mit sehr hoher Genauigkeit vorhersagen.

Weblinks

• Spektrallinien